- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему История тригонометрии
Содержание
- 2. СодержаниеОпределения ИсторияСинус, косинус, тангенсДальнейшее развитие Аналитическая теорияСписок литературы
- 3. ОпределенияТригономе́трия-от греч. τρίγονο (треугольник) и греч. μετρειν
- 4. ИсторияТригонометрия возникла из практических нужд человека. С
- 5. Древняя ГрецияДревнегреческие математики в своих построениях, связанных
- 6. Средневековая Индия Другие источники сообщают, что именно
- 7. СинусДлительную историю имеет понятие синус. Фактически различные
- 8. Косинус и тангенсСлово косинус намного моложе. Косинус
- 9. Дальнейшее развитиеДальнейшее развитие тригонометрия получила в трудах
- 10. Аналитическая теорияАналитическая теория тригонометрических функций в основном
- 11. Скачать презентацию
- 12. Похожие презентации
СодержаниеОпределения ИсторияСинус, косинус, тангенсДальнейшее развитие Аналитическая теорияСписок литературы









Слайд 2
Содержание
Определения
История
Синус, косинус, тангенс
Дальнейшее развитие
Аналитическая теория
Список литературы
Слайд 3
Определения
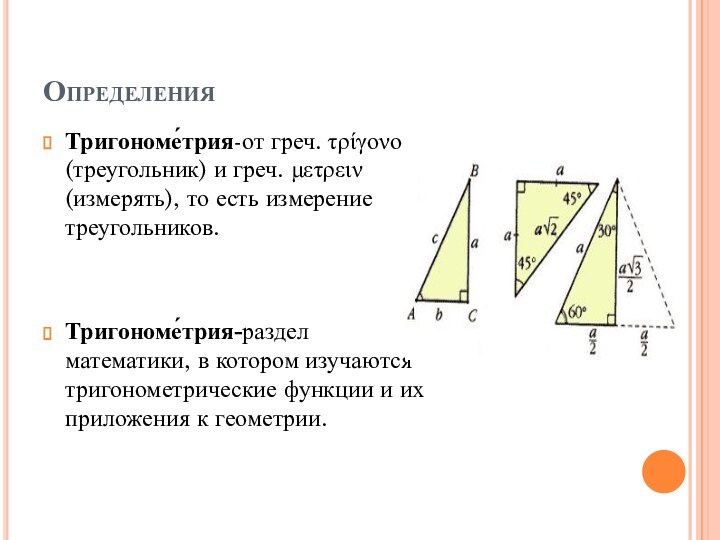
Тригономе́трия-от греч. τρίγονο (треугольник) и греч. μετρειν (измерять),
то есть измерение треугольников.
и их приложения к геометрии.
Слайд 4
История
Тригонометрия возникла из практических нужд человека. С ее
помощью можно определить расстояние до недоступных предметов и, вообще
существенно упрощать процесс геодезической съемки местности для составления географических карт.Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Слайд 5
Древняя Греция
Древнегреческие математики в своих построениях, связанных с
измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде,
опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.
Слайд 6
Средневековая Индия
Другие источники сообщают, что именно замена хорд
синусами стала главным достижением Средневековой Индии. Такая замена позволила
вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются так:
sin2α + cos2α = 1
Слайд 7
Синус
Длительную историю имеет понятие синус. Фактически различные отношения
отрезков треугольника и окружности встречаются уже в III веке
до н.э. в работах великих математиков Древней Греции Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус , например, изучался как полухорда, на которую опирается центральный угол величиной , или как хорда удвоенной дуги.
Слайд 8
Косинус и тангенс
Слово косинус намного моложе. Косинус это
сокращение латинского выражения completely sinus, т. е. “дополнительный синус”.
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов.





























