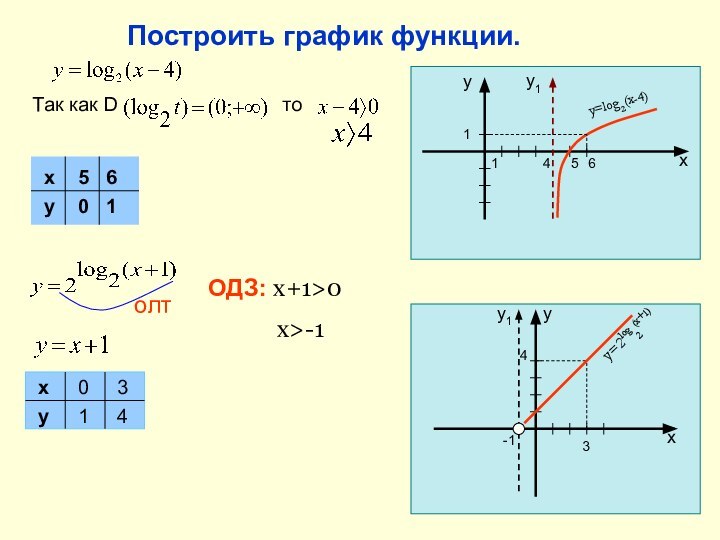
основанием a.
Построим графики функций y=log2x и y=log½x
Основные свойства функции
D(loga)=(0;+)
E(loga)=(-;+)
Логарифмическая
функция на всей области определения возрастает (при a>0) или убывает (при 0y=log2x
y=log½x