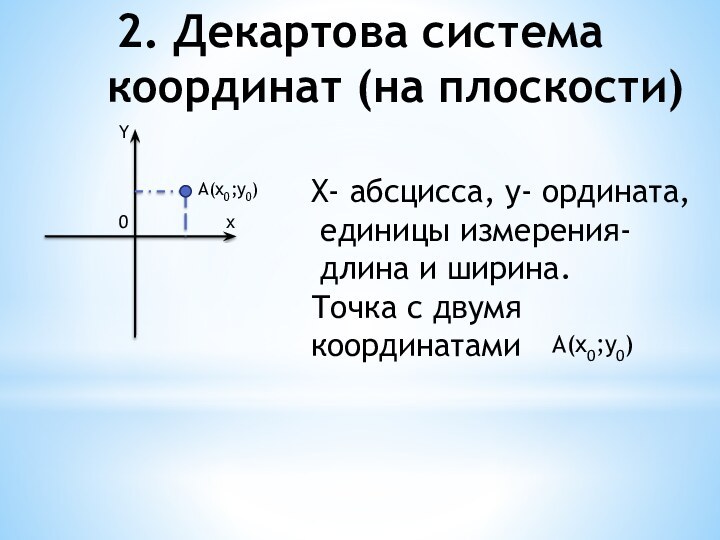
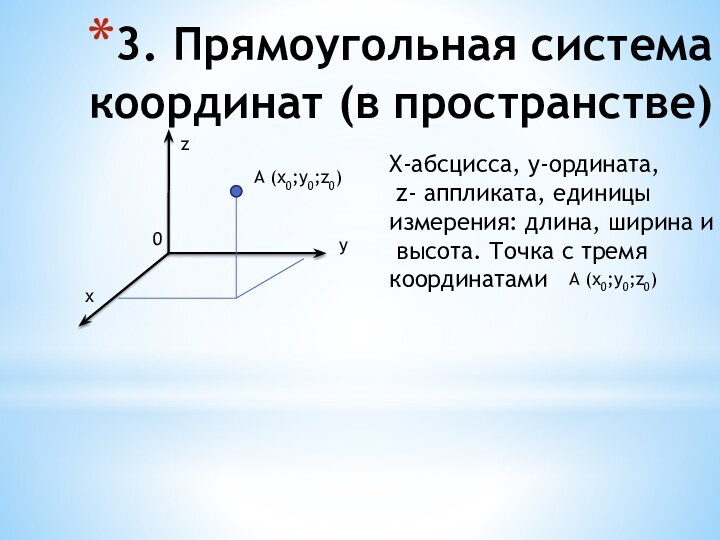
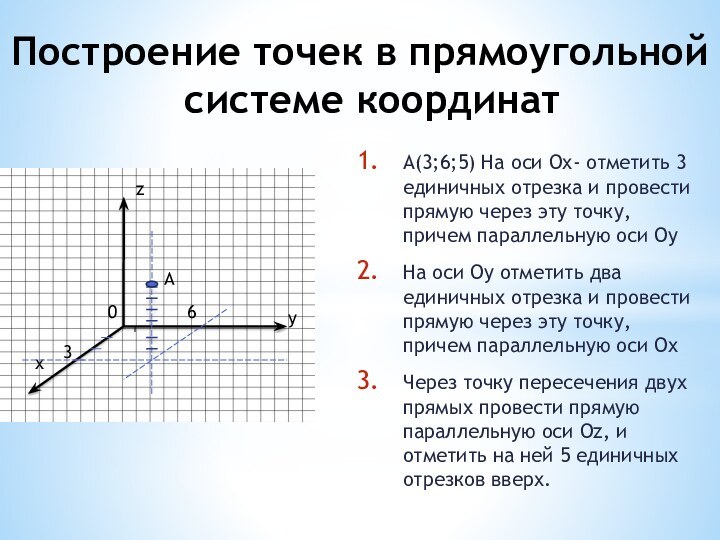
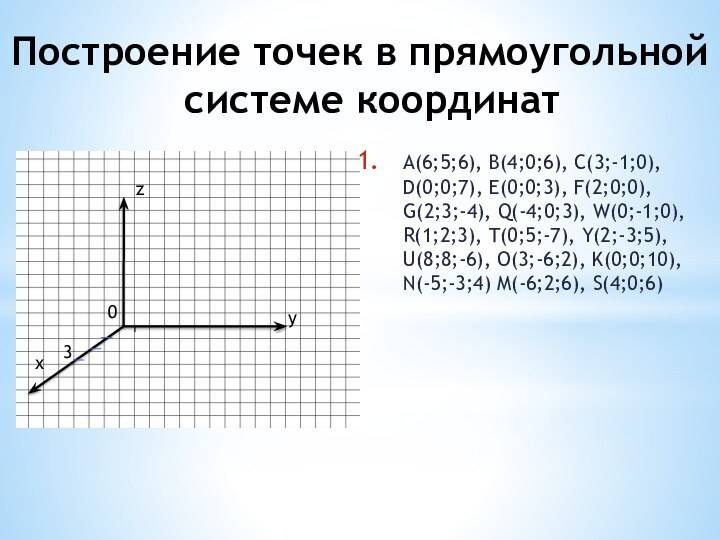
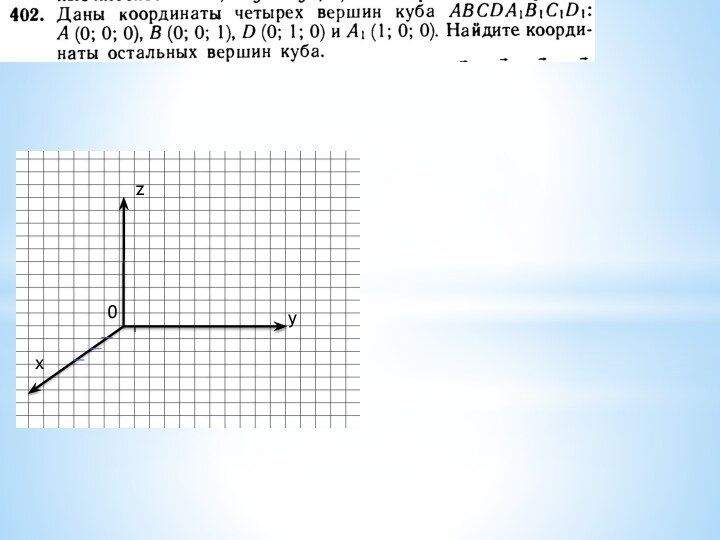
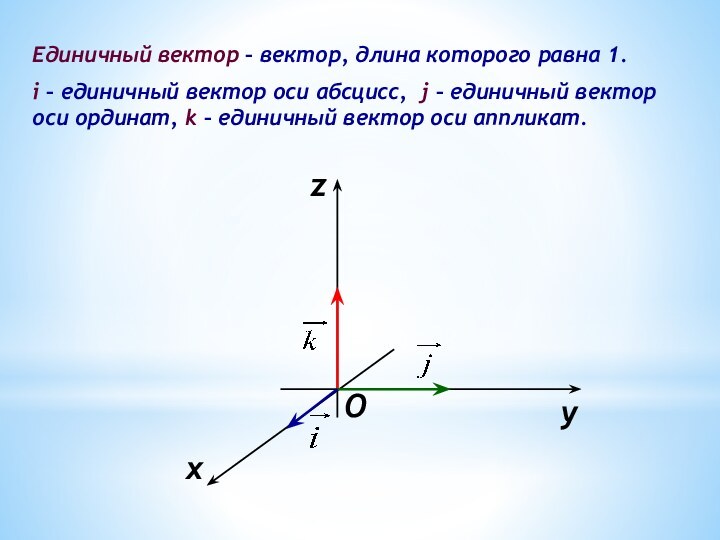
координатами вектора и координатами точек
Простейшие задачи в координатах
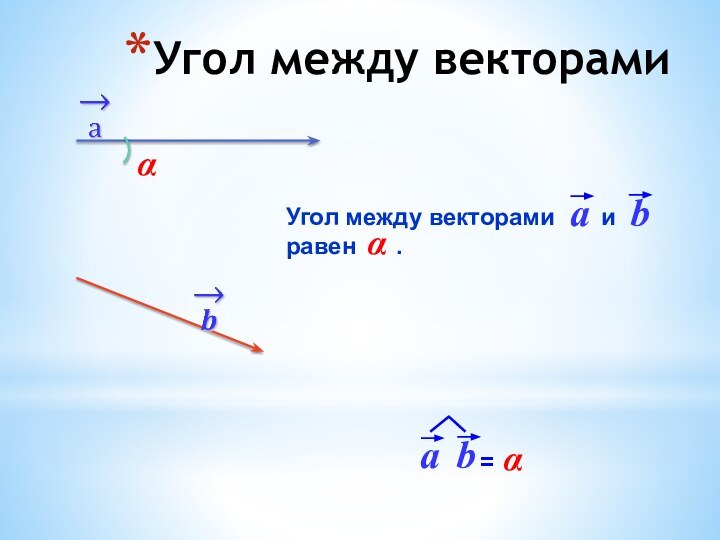
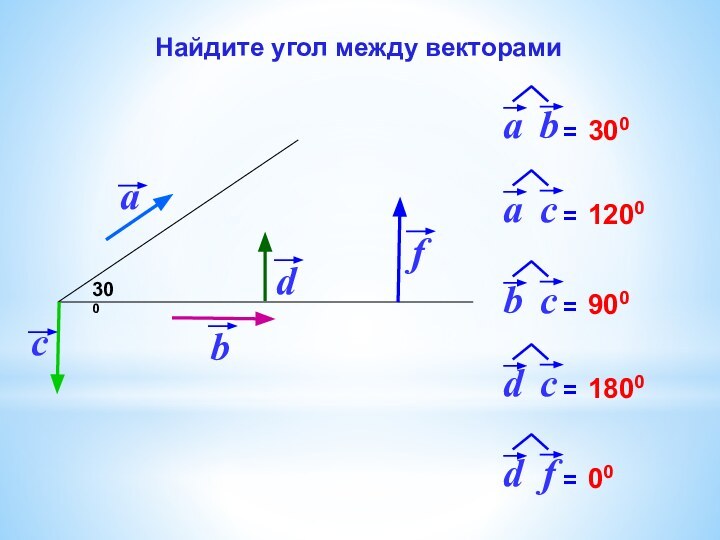
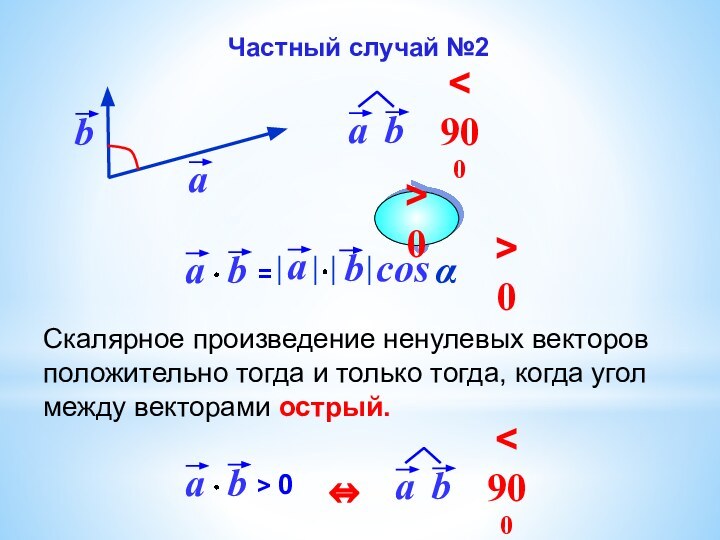
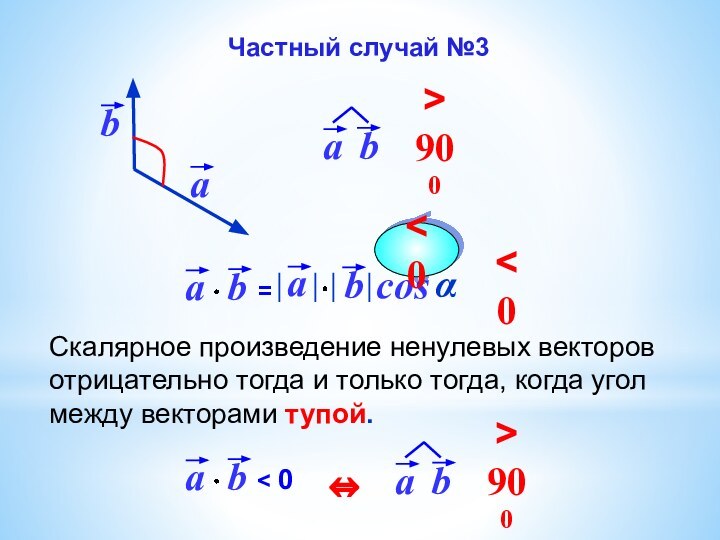
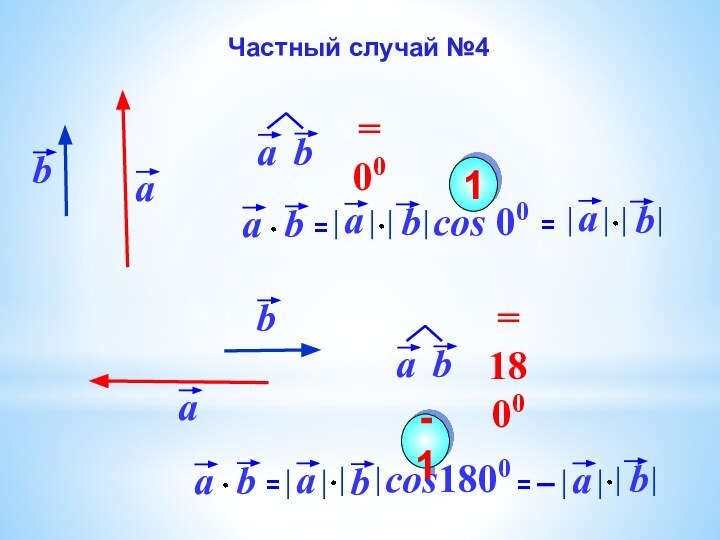
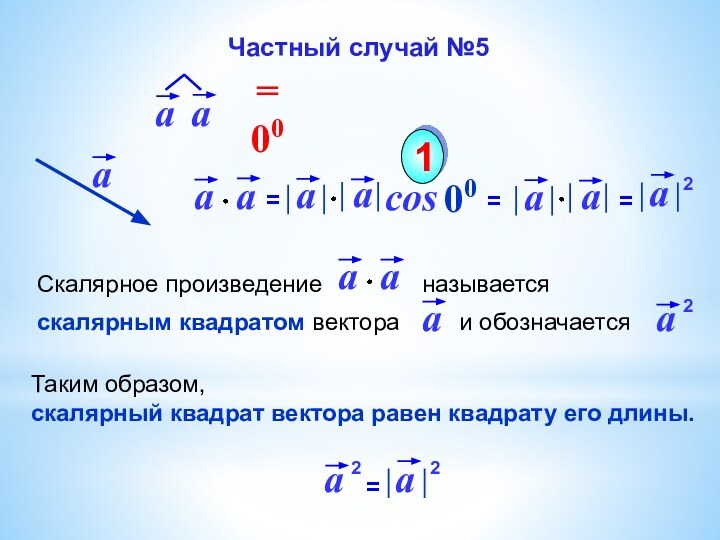
Угол между
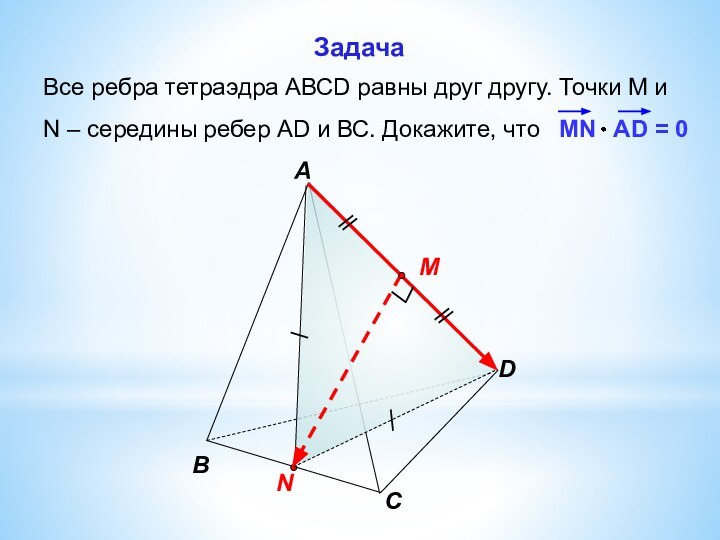
векторамиСкалярное произведение векторов
Вычисление углов между прямыми и плоскостями
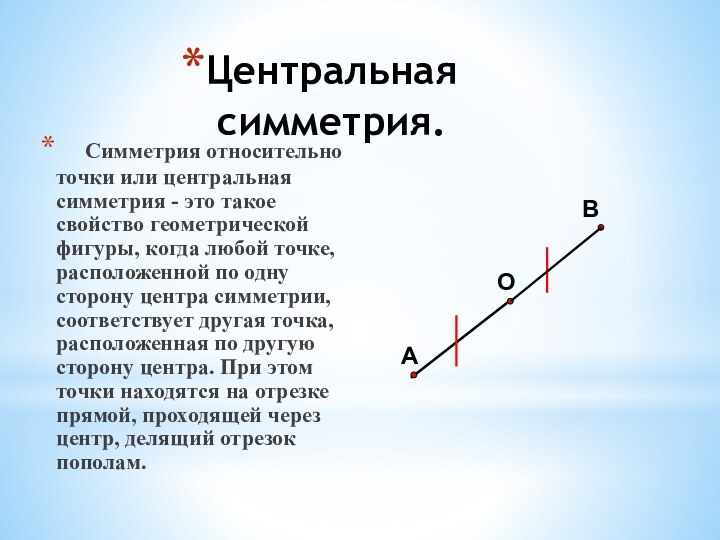
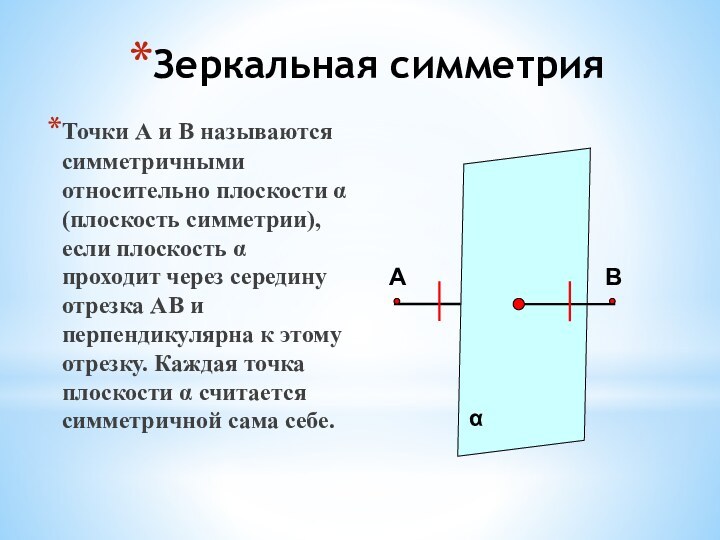
Движения. Центральная симметрия. Осевая симметрия.