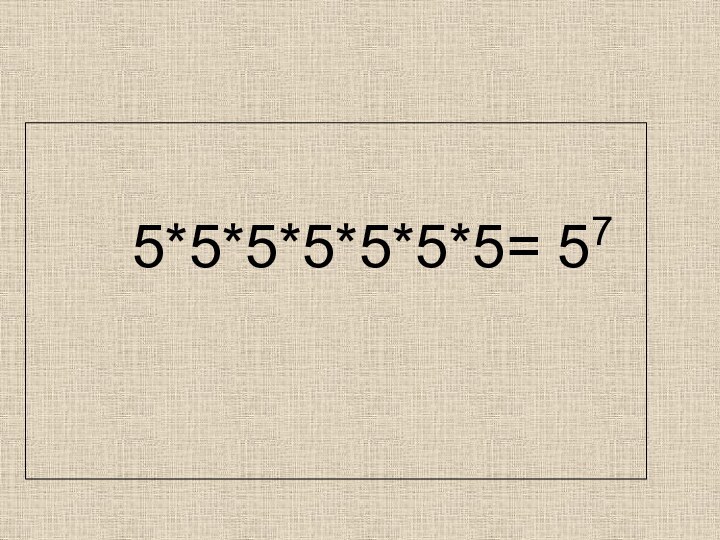Слайд 3
5
5 – основание степени
7- показатель степени
Слайд 4
Степенью числа а с натуральным показателем n, большим
1, называется произведение n множителей, каждый из которых равен
a.
Степенью числа а с показателем 1 называется само число а.
Слайд 5
а
«а в степени n»
«n- я степень
числа а».
По определению степени:
а¹ = а, а²=аа, а³= ааа.
а = аа…а
n раз
Слайд 6
3 = 3*3*3*3=81;
0³=0*0*0= 0;
(-6)³=(-6)*(-6)*(-6)=-216; 9¹=9.
Слайд 7
При возведении в степень положительного числа получается положительное
число; при возведении в степень нуля получается нуль.
Слайд 8
При возведении в степень отрицательного числа может получится
как положительное, так и отрицательное.
(-2)¹=-2
(-2) ²=(-2)*(-2)=4
(-2) ³=(-2)*(-2)*(-2)=-8
(-2)
= (-2)*(-2)*(-2)*(-2)=16
(-2) = (-2)*(-2)*(-2)*(-2)*(-2)=-32
Слайд 9
Степень отрицательного числа с четным показателем- положительное число.
Степень
отрицательного числа с нечетным показателем- отрицательное число.
Слайд 10
Квадрат любого числа есть положительное число или нуль,
т.е. а²>0 при любом а.
Слайд 11
ПРИМЕР 1.
Найдём значение выражения 4*10³
1)10³=10*10*10=1000;
2)4*1000=4000.
3) 4*10³=4000.
Слайд 12
ПРИМЕР 2.
Найдём значение выражения:
-2 6 +(-3) 4
1)
-26 =-64;
2)(-3)4 =81;
3)-64+81=17.