Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Основы комбинаторики

Содержание

2. Правило произведенияПусть объект а1 можно выбрать n1,
3. Составление слова из восьми букв можно представить
4. Пример 2. Сколько четырехбуквенных «слов» можно составить
5. Пример 3. Сколькими способами можно поставить на
6. Выбор объекта а1 - поля для белой
7. Пример 5. Сколь различных слов можно получить, переставляя буквы слова «комбинаторика»?
8. В слове «комбинаторика» 13 букв. Если бы
9. Пример 6. Сколько существует четырехзначных чисел, у
10. Всего нечетных цифр — пять, поэтому выбор
11. Правило суммы Если объект а
12. Пример 7. Сколько различных пар можно образовать
13. Выбор пары костей — это выбор двух
14. § 2. Размещения и перестановки
15. Определение. Всякая упорядоченная выборка объема k из
16. Определение. Размещение из n элементов по n
17. Справедлива формула
18. На первое место в выборке можно поместить
19. An = n(n - 1)...(n - k+1)·(n-k)!=
20. Пример 9. Сколько шестизначных чисел, кратных 5,
21. Последней цифрой искомого числа может быть 0
22. Пример 10. Сколькими способами можно расставить на
23. § 3. Сочетания
24. Определение. Всякая неупорядоченная выборка объема к из
25. Из любого набора,содержащего к элементов, можно с
27. Пример 11. Хоккейная команда состоит из 2
28. Вратаря можно выбрать
29. Пример 12. На плоскости проведены n прямых,
30. Число точек пересечения прямых равно числу способов
31. Пример 13. Для проведения
32. Задачи для первого варианта можно выбрать
33. По правилу произведения получаем число
34. Свойства чисел :1°.
35. Свойство 1°
36. Свойство 2°
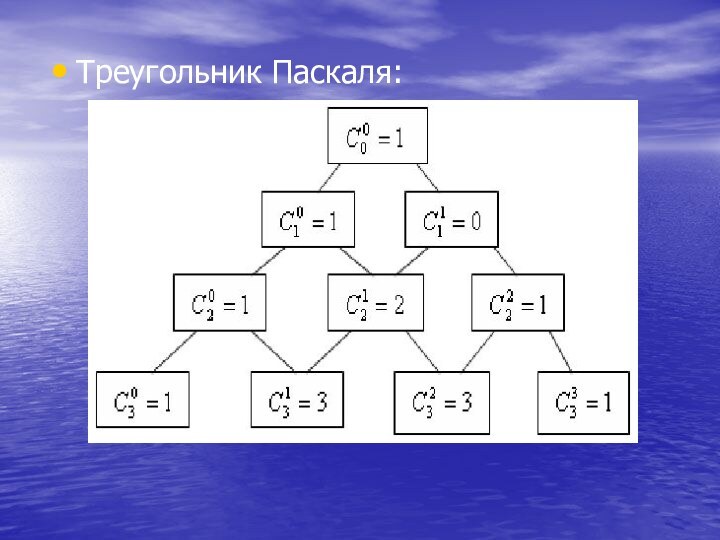
38. Треугольник Паскаля:
39. Свойство 3° Положим Так как
40. § 4. Бином Ньютона
41. (a + b) =a +2ab + b
43. Если в формуле (5) взять а =b
45. Формула (6) называется полиномиальной. Например, (а +
46. Пример 14. Найти n, если известно,
47. В n-й строке треугольника Паскаля два коэффициента
48. Следовательно, равно тогда и
49. Пример 15. Найти коэффициент при х
50. В силу формулы (6)
51. 2) Обозначим через
52. Литература1. Кутасова А.Д., Пиголкина Т.С, Чехлов В.И., Яковлева
53. Контрольные вопросыСколько делителей у числа 2004
54. Скачать презентацию
55. Похожие презентации

Правило произведенияПусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными способами,..., после каждого выбора объектов а1, а2,..., аp-1 объект аp можно выбрать

§ 1. Примеры комбинаторных задач и общие принципы комбинаторики

Составление слова из восьми букв можно представить как заполнение буквами клеток следующей

Пример 2. Сколько четырехбуквенных «слов» можно составить из карточек «в», «е», «ч»,

Пример 3. Сколькими способами можно поставить на шахматную доску белую и черную

Выбор объекта а1 - поля для белой ладьи - может быть сделан

Пример 5. Сколь различных слов можно получить, переставляя буквы слова «комбинаторика»?

В слове «комбинаторика» 13 букв. Если бы все они были различны, то,

Пример 6. Сколько существует четырехзначных чисел, у которых все цифры нечетные? Сколько

Всего нечетных цифр — пять, поэтому выбор к-й цифры числа может быть

Правило суммы Если объект а можно выбрать т различными способами,

Пример 7. Сколько различных пар можно образовать из 28 костей домино так,

Выбор пары костей — это выбор двух карточек вида a1b1, a2b2,где можно

Определение. Всякая упорядоченная выборка объема k из множества, состоящего из n элементов,

Определение. Размещение из n элементов по n называется перестановкой из n элементов

На первое место в выборке можно поместить любой из n элементов, на

Пример 9. Сколько шестизначных чисел, кратных 5, можно составить из цифр 0,

Последней цифрой искомого числа может быть 0 или 5. В первом случае

Пример 10. Сколькими способами можно расставить на книжной полке десятитомник Пушкина так,

Определение. Всякая неупорядоченная выборка объема к из множества, состоящего из n элементов

Из любого набора,содержащего к элементов, можно с помощью перестановок получить k! упорядоченных

Пример 11. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10

Вратаря можно выбрать способами, защитников

Пример 12. На плоскости проведены n прямых, среди которых нет ни одной

Число точек пересечения прямых равно числу способов выбора неупорядоченной пары прямых,

Пример 13. Для проведения письменного экзамена

Задачи для первого варианта можно выбрать способами. После этого

Свойство 3° Положим Так как каждое число строки с номером

Если в формуле (5) взять а =b = 1, то получится известное

Формула (6) называется полиномиальной. Например, (а + b + с) = а

Пример 14. Найти n, если известно, что в разложении (1 +

В n-й строке треугольника Паскаля два коэффициента равны в том и только

Следовательно, равно тогда и только тогда, когда 12 =

Пример 15. Найти коэффициент при х в разложении

Литература1. Кутасова А.Д., Пиголкина Т.С, Чехлов В.И., Яковлева Т.Х., Пособие по математике для

Контрольные вопросыСколько делителей у числа 2004 ?Сколько диагоналей в выпуклом 2004-угольнике?Сколько

Задачи1(3). Сколько различных слов можно получить, переставляя буквы в слове «параллелограмм»?2(4). Сколькими

Слайды презентации

Слайд 2 Правило произведения
Пусть объект а1 можно выбрать n1, различными

Правило произведенияПусть объект а1 можно выбрать n1, различными способами, после каждого

способами, после каждого выбора объекта а1 объект а2 можно

выбрать n2 различными способами,..., после каждого выбора объектов а1, а2,..., аp-1 объект аp можно выбрать nр различными способами. Тогда количество способов, которыми можно выбрать а1, а2, ..., аp равно n1n2...np.

Слайд 3 Составление слова из восьми букв можно представить как

Составление слова из восьми букв можно представить как заполнение буквами клеток

заполнение буквами клеток следующей таблицы:

1 2

3 4 5 6 7 8
На первое место можно поставить любую из восьми букв, на второе - любую из семи оставшихся и т.д. вплоть до заполнения единственным способом клетки № 8 последней оставшейся буквой. Число способов заполнения таблицы будет равно 8·7·6·5·4·3·2·1=8!
Напомним, что символом п! (читается «эн факториал») обозначается произведение всех натуральных чисел от 1 до п: n!=1·2·...·(n-1)·n.
Ответ: n!= 1 • 2 • ...• (n -1) • п.

Слайд 4 Пример 2. Сколько четырехбуквенных «слов» можно составить из

Пример 2. Сколько четырехбуквенных «слов» можно составить из карточек «в», «е»,

карточек «в», «е», «ч», «н», «о», «с», «т», «ь»?
Пусть

ак - к -я буква слова (к =1,2,3,4). Тогда n1 = 8,n2 = 7, n3=6, nА = 5 и по правилу произведения сразу получаем ответ:
8·7·6·5 = 1680.
Ответ: 1680.

Слайд 5 Пример 3. Сколькими способами можно поставить на шахматную

Пример 3. Сколькими способами можно поставить на шахматную доску белую и

доску белую и черную ладью так, чтобы они не

били друг друга?

Слайд 6 Выбор объекта а1 - поля для белой ладьи

Выбор объекта а1 - поля для белой ладьи - может быть

- может быть сделан n1 = 64 способами. Независимо

от выбора этого поля белая ладья бьет 15 полей, поэтому для черной ладьи остается 64-15 =49 полей: n2 = 49.
Ответ: число расстановок ладей равно 64 · 49 = 3136.

Слайд 7 Пример 5. Сколь различных слов можно получить, переставляя

буквы слова «комбинаторика»?

Слайд 8 В слове «комбинаторика» 13 букв. Если бы все

В слове «комбинаторика» 13 букв. Если бы все они были различны,

они были различны, то, переставляя их, можно было бы

получить 13! слов. Но в нашем слове буквы к, о, и, а встречаются по два раза. Обозначим их к1,к2,о1,о2,и1,и2,а1,а2. Ясно, что слова, отличающиеся перестановкой букв к1ик2 - одинаковые, так что 13! Слов разбиваются на пары одинаковых. Следовательно, если мы не различаем к1 и к2, то число всех слов будет равно 13!/2!. Но эта совокупность также разбивается на пары одинаковых с точки зрения буквы “о„ слов и т.д.
13! 13!
Ответ: = = —.
2!2!2!2! 16

Слайд 9 Пример 6. Сколько существует четырехзначных чисел, у которых

Пример 6. Сколько существует четырехзначных чисел, у которых все цифры нечетные?

все цифры нечетные? Сколько существует четырехзначных чисел, в записи

которых есть хотя бы одна четная цифра?

Слайд 10 Всего нечетных цифр — пять, поэтому выбор к-й

Всего нечетных цифр — пять, поэтому выбор к-й цифры числа может

цифры числа может быть сделан nк =5 способами (к

=1, 2, 3, 4) а количество четырехзначных чисел, у которых все цифры нечетные, равно 5·5·5·5 = 625.

Слайд 11 Правило суммы

Если объект а можно

выбрать т различными способами, а объект b можно

выбрать n различными способами, причем результаты выбора объектов а и b никогда не совпадают, то выбор “либо а, либо b» можно осуществить т + n различными способами.

Слайд 12 Пример 7. Сколько различных пар можно образовать из

Пример 7. Сколько различных пар можно образовать из 28 костей домино

28 костей домино так, чтобы кости, входящие в пару,

можно было приложить друг к другу?

Слайд 13 Выбор пары костей — это выбор двух карточек

Выбор пары костей — это выбор двух карточек вида a1b1, a2b2,где

вида a1b1, a2b2,
где можно считать, что а ≤ b.
Выберем

первую кость - это можно сделать 28 способами, из них в 7 случаях кость окажется дублем, т.е. кость вида aa, а в 21 случае — кость вида ab, а < b . В первом случае вторую кость можно выбрать 6 способами, а число способов выбора пары костей по правилу произведения равно 7 · 6 = 42 .
Во втором случае вторую кость можно выбрать 12 способами — 6 костей вида a|* и 6 костей вида *|а ,а число способов выбора пары равно 21·12 = 252.
Следовательно по правилу суммы всего получается 42 + 252 = 294 способа выбора упорядоченной пары.
Ответ: 147 пар.

Слайд 14

§ 2. Размещения и перестановки

Слайд 15 Определение. Всякая упорядоченная выборка объема k из множества,

Определение. Всякая упорядоченная выборка объема k из множества, состоящего из n

состоящего из n элементов, называется размещением из n элементов

по k элементов и обозначается через Аn .

Слайд 16 Определение. Размещение из n элементов по n называется

Определение. Размещение из n элементов по n называется перестановкой из n

перестановкой из n элементов и обозначается через Рn .

Слайд 17 Справедлива формула

Справедлива формула Аn =n (n-1)...(n - к

Аn =n (n-1)...(n - к + 1)

где 1 ≤ к ≤ n.

Слайд 18 На первое место в выборке можно поместить любой

На первое место в выборке можно поместить любой из n элементов,

из n элементов, на второе - любой из (n

- 1) оставшихся и т.д. После выбора элементов на(k-1)-е место останется n-(к-1) = n-к+1 элемен-

1 2 k-1 k
тов, любой из которых можно поместить на к-е место. По правилу произведения получаем
Аn = (n-1)...(n - к + 1)
В частности,
Рn=An =n(n-1)… ·2·1 = n! (2)

Слайд 19 An = n(n - 1)...(n - k+1)·(n-k)!=

n!

(n-к)! (n-к)!

Слайд 20 Пример 9. Сколько шестизначных чисел, кратных 5, можно

Пример 9. Сколько шестизначных чисел, кратных 5, можно составить из цифр

составить из цифр 0, 1,2, ..., 9 при условии,

что цифры в записи числа не повторяются?

Слайд 21 Последней цифрой искомого числа может быть 0 или

Последней цифрой искомого числа может быть 0 или 5. В первом

5. В первом случае остальные пять цифр можно выбирать

из множества {1,2, ..., 9}
9!
и число вариантов равно А9 = — = 15120. Если число
4!
oканчивается цифрой 5, то в качестве первой цифры можно взять любую из восьми цифр 1, 2, 3, 4, 6, 7, 8, 9 - нельзя использовать 0, т.к. число должно быть шестизначным. Цифры со второй по четвертую можно выбрать
A8 = 1680 различными способами. Следовательно, по правилу произведения имеется 8·A8 чисел, оканчивающихся цифрой 5. По правилу суммы находим, сколько существует чисел, удовлетворяющих условию задачи.
А9 +8·A8 = 28560.
Ответ: 28560.

Слайд 22 Пример 10. Сколькими способами можно расставить на книжной

Пример 10. Сколькими способами можно расставить на книжной полке десятитомник Пушкина

полке десятитомник Пушкина так, чтобы том 2 стоял рядом

с томом 1 и справа от него?
Ответ: 9!

Слайд 23 § 3. Сочетания

Слайд 24 Определение. Всякая неупорядоченная выборка объема к из множества,

Определение. Всякая неупорядоченная выборка объема к из множества, состоящего из n

состоящего из n элементов (к≤n), называется сочетанием из n

элементов по к элементов и обозначается через Сn .

Слайд 25 Из любого набора,содержащего к элементов, можно с помощью

Из любого набора,содержащего к элементов, можно с помощью перестановок получить k!

перестановок получить k! упорядоченных выборок объема k, поэтому

Откуда
(4)

Слайд 26

Слайд 27 Пример 11. Хоккейная команда состоит из 2 вратарей,

Пример 11. Хоккейная команда состоит из 2 вратарей, 7 защитников и

7 защитников и 10 нападающих. Сколькими способами тренер может

образовать стартовую шестерку, состоящую из вратаря, двух защитников и трех нападающих?

Слайд 28 Вратаря можно выбрать

способами, защитников -
способом,

нападающих –
способами. Всего, по правилу произведения, существует 2 · 21 · 120 = 5040 способов выбора стартовой шестерки.
Ответ: 5040.

Слайд 29 Пример 12. На плоскости проведены n прямых, среди

Пример 12. На плоскости проведены n прямых, среди которых нет ни

которых нет ни одной пары параллельных прямых и ни

одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения этих прямых и число треугольников, образованных этими прямыми.

Слайд 30 Число точек пересечения прямых равно числу способов выбора

неупорядоченной пары прямых, т.е. . Аналогично,

каждый треугольник определяется тройкой прямых, поэтому общее число треугольников равно .
Ответ: и .

Слайд 31 Пример 13. Для проведения

письменного экзамена по комбинаторике надо составить 4

варианта по 7 задач в каждом. Сколькими способами можно разбить 28 задач на 4 варианта?

Слайд 32 Задачи для первого варианта можно выбрать

Задачи для первого варианта можно выбрать способами. После этого останется

способами. После этого останется 21 задача, так что

второй вариант можно составить способами. Для третьего варианта задачи можно выбрать способами, а для четвертого - = 1 способом.

Слайд 33 По правилу произведения получаем число

. Но

так как варианты равноправны, то полученное число надо разделить на 4!
Ответ: =

Слайд 34 Свойства чисел :
1°.

, если 0≤к≤n;
2°.

, если 0≤к≤n+1;
3°.

Слайд 35 Свойство 1°

Слайд 36 Свойство 2°

Слайд 37

Слайд 38 Треугольник Паскаля:

Слайд 39 Свойство 3°
Положим

Так как каждое

Свойство 3° Положим Так как каждое число строки с номером п

число строки с номером п входит в качестве слагаемого

в два соседних числа следующей строки, то
Sn+1 = 2Sn .
Следовательно, т.к. S0=1.

Слайд 40 § 4. Бином Ньютона

Слайд 41 (a + b) =a +2ab + b

и (a + b)

= а +3а b + 3ab +b .

Слайд 42

Слайд 43 Если в формуле (5) взять а =b =

Если в формуле (5) взять а =b = 1, то получится

1, то получится известное нам свойство 3° чисел

, а если взять а=1, b = -1, то получим еще одно комбинаторное равенство:

Слайд 44

Слайд 45 Формула (6) называется полиномиальной. Например,
(а + b

Формула (6) называется полиномиальной. Например, (а + b + с) =

+ с) = а + b + с +

3(а b + а с + b а + b с + с а + c b ) + 6abc.

Слайд 46 Пример 14. Найти n, если известно, что

в разложении (1 + x)
коэффициенты при х

и х равны.

Слайд 47 В n-й строке треугольника Паскаля два коэффициента равны

В n-й строке треугольника Паскаля два коэффициента равны в том и

в том и только том случае, когда они занимают

клетки, равноудаленные от крайних. Действительно, треугольник Паскаля симметричен: , а при движении от края к середине строки коэффициенты возрастают: при
и при

Слайд 48 Следовательно, равно тогда и только

Следовательно, равно тогда и только тогда, когда 12 = n-5,

тогда, когда 12 = n-5, т.е. n= 17.
Ответ: n

= 17.

Слайд 49 Пример 15. Найти коэффициент при х в

разложении

(1 + х +х ) .

Слайд 50 В силу формулы (6)

=
Так как уравнение

5k2 + 9к3 =19 имеет только одно решение в неотрицательных числах k2=2, k3 = 1, то коэффициент при х равен

Слайд 51 2) Обозначим через

. Тогда

Рассмотрим k-е слагаемое (0≤k≤30):

Такое слагаемое будет содержать х , если для некоторого т выполняется равенство 5k + 4m = 19. Ясно, что это возможно только при k=3 и т=1. Следовательно, коэффициент при х равен =12180.

Слайд 52 Литература
1. Кутасова А.Д., Пиголкина Т.С, Чехлов В.И., Яковлева Т.Х., Пособие

Литература1. Кутасова А.Д., Пиголкина Т.С, Чехлов В.И., Яковлева Т.Х., Пособие по математике

по математике для поступающих в вузы. /под ред. Г.Н. Яковлева

- M.: Наука, 1988.
2. Виленкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975.
3. Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. — Киров, 1994.

Слайд 53 Контрольные вопросы
Сколько делителей у числа 2004 ?
Сколько

диагоналей в выпуклом 2004-угольнике?
Сколько различных натуральных решений имеет неравенство

n+m≤2004?
4. Чему равен коэффициент при х y в выражении (х + у)
после раскрытия скобок?
5. С помощью соответствующей строки треугольника Паскаля выпишите формулу для вычисления (а-b) .