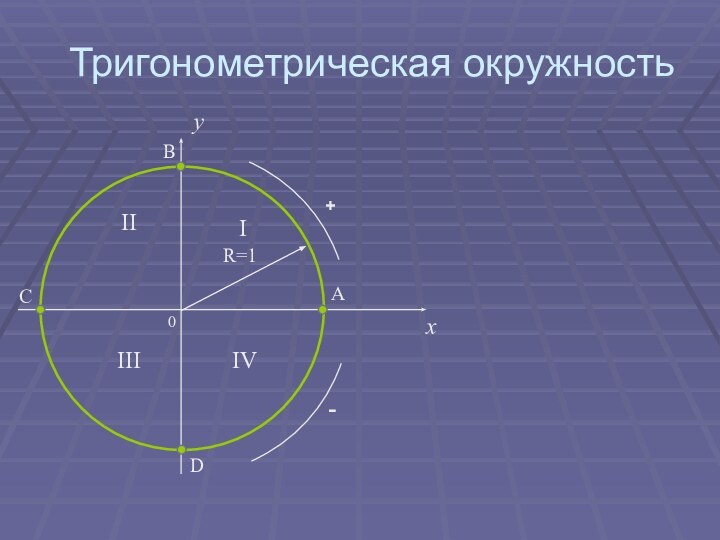
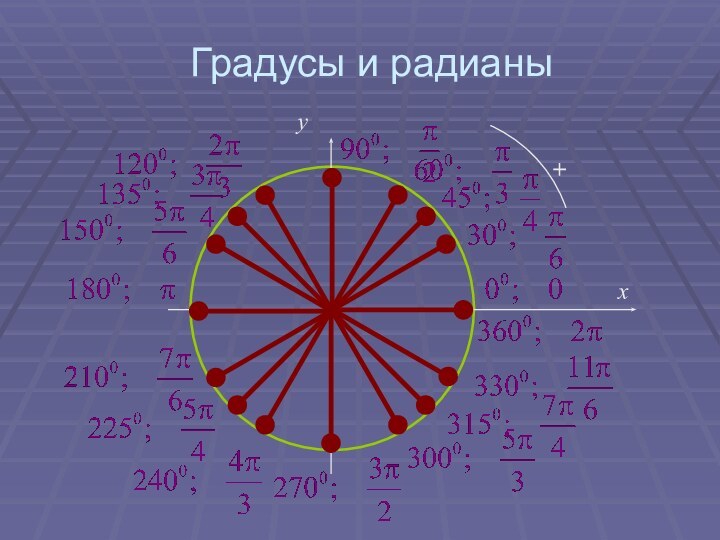
астрономии. Древнегреческие ученые разработали «тригонометрию хорд».
Древнеиндийские ученые заменили
хорды синусами.В VIII веке математики Востока превратили тригонометрию в самостоятельную математическую дисциплину. Ими были введены другие тригонометрические функции и составлены таблицы.
Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л.Эйлера.