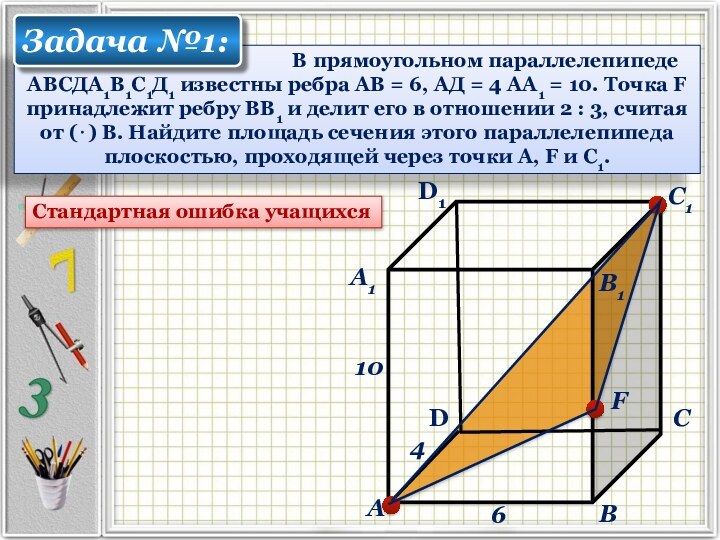
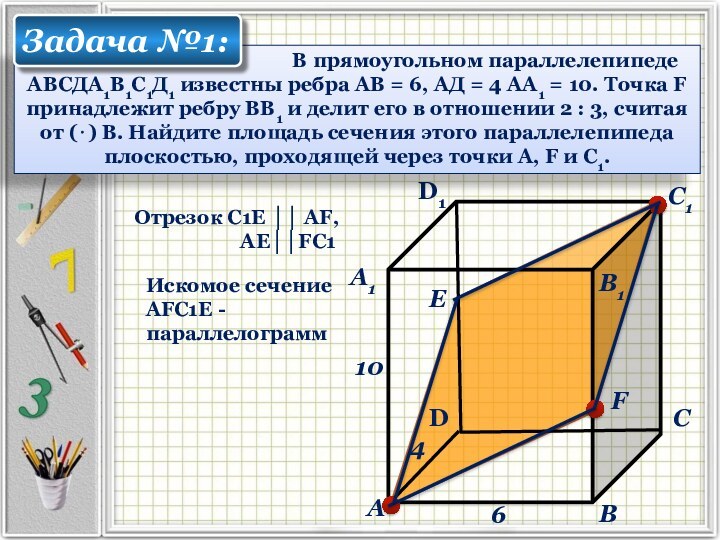
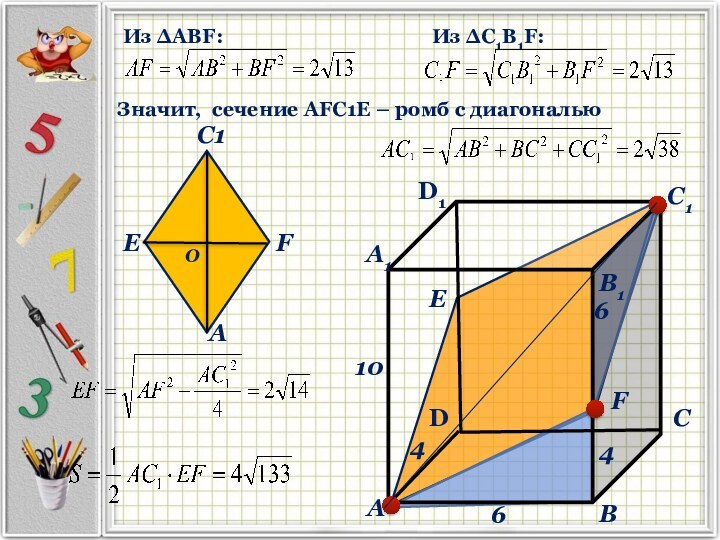
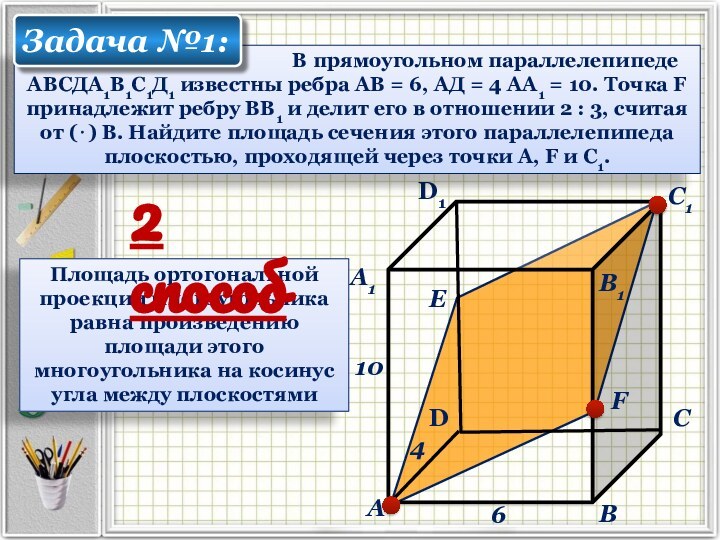
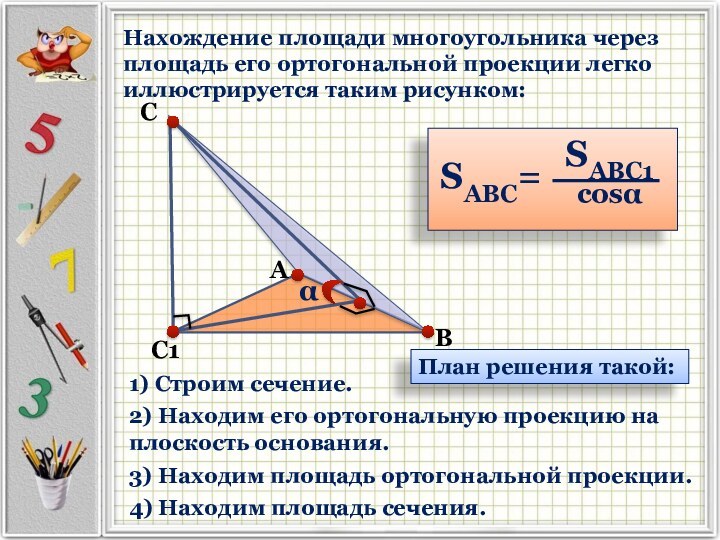
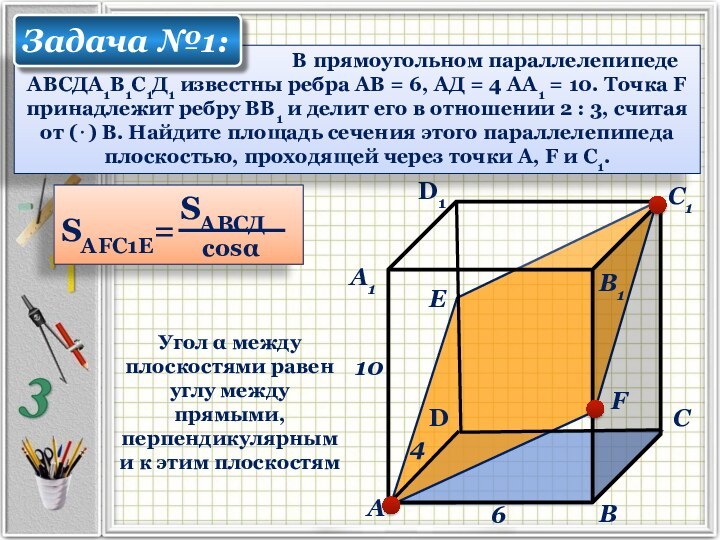
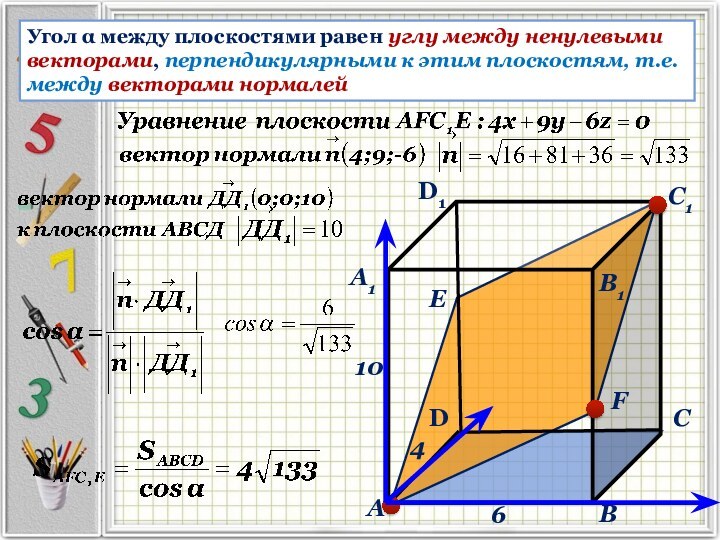
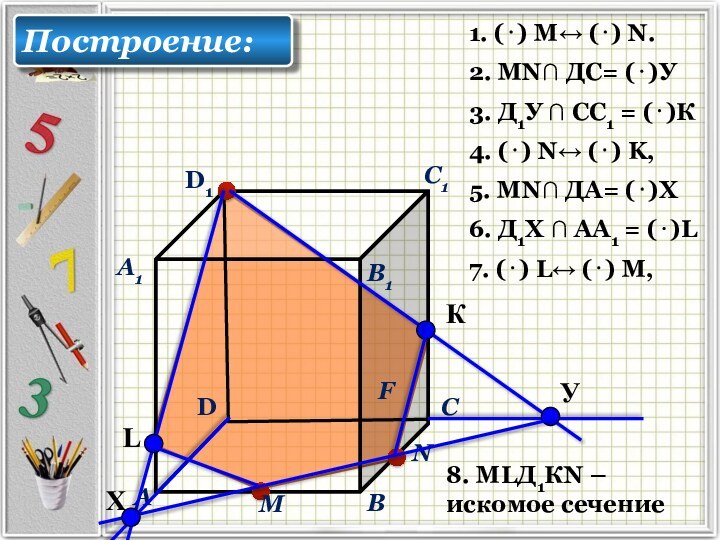
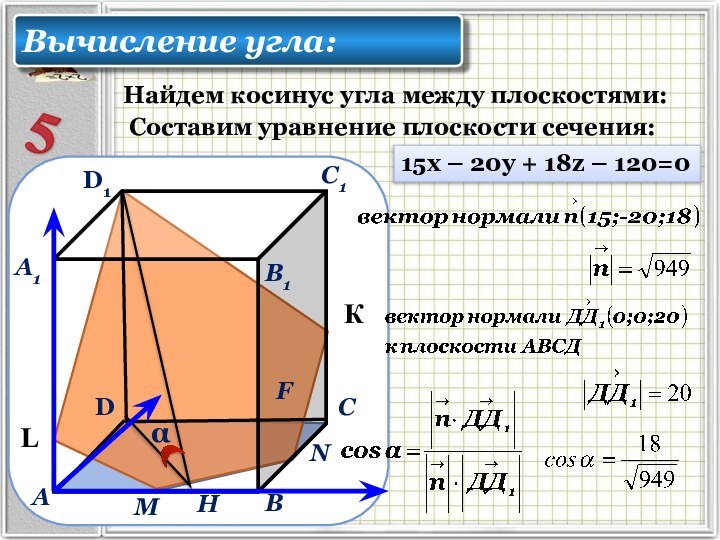
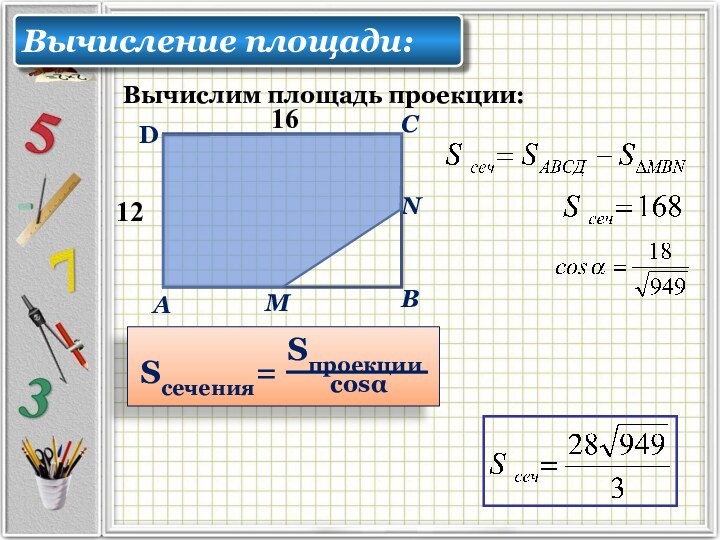
В прямоугольном параллелепипеде АВСДА1В1С1Д1 известны ребра АВ = 6, АД = 4 АА1 = 10. Точка F принадлежит ребру ВВ1 и делит его в отношении 2 : 3, считая от (⋅) В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, F и С1.
Стандартная ошибка учащихся
Задача №1: