Презентация на тему Прототипы задач по геометрии

- 5 заданий, в час-
ти 2 - 3 задания.
Модуль

- 5 заданий, в час-
ти 2 - 3 задания.
Вашему

Задача № 9. 1Задача № 9. 1, 2Задача № 9. 1, 2, 3Задача № 9. 1, 2, 3, 4Задача № 9. 1, 2, 3, 4, 5Задача № 9. 1, 2, 3, 4, 5, 6Задача № 9. 1, 2, 3, 4, 5, 6, 7

Задача № 10. 1Задача № 10. 1, 2Задача № 10. 1, 2, 3Задача № 10. 1, 2, 3, 4Задача № 10. 1, 2, 3, 4, 5Задача № 10. 1, 2, 3, 4, 5, 6Задача № 10. 1, 2, 3, 4, 5, 6, 7

Задача № 11. 1Задача № 11. 1, 2Задача № 11. 1, 2, 3Задача № 11. 1, 2, 3, 4Задача № 11. 1, 2, 3, 4, 5Задача № 11. 1, 2, 3, 4, 5, 6Задача № 11. 1, 2, 3, 4, 5, 6, 7

Задача № 12. 1Задача № 12. 1, 2Задача № 12. 1, 2, 3Задача № 12. 1, 2, 3, 4Задача № 12. 1, 2, 3, 4, 5Задача № 12. 1, 2, 3, 4, 5, 6Задача № 12. 1, 2, 3, 4, 5, 6, 7

Задача № 13. 1Задача № 13. 1, 2Задача № 13. 1, 2, 3Задача № 13. 1, 2, 3, 4Задача № 13. 1, 2, 3, 4, 5Задача № 13. 1, 2, 3, 4, 5, 6Задача № 13. 1, 2, 3, 4, 5, 6, 7

сумма углов равна 180°

117°=6°


Модуль «ГЕОМЕТРИЯ» № 9 (2)

углом треугольника
Сумма смежных углов углов равна 180°

В треугольнике сумма

это луч, который делит угол пополам

В треугольнике сумма углов

другого. Найти больший из них.
Повторение (2)
∠А+∠D=180°

Пусть ∠А=х°, тогда∠D=(х+46)°

х+х+46=180

2х=134

х=67

∠D

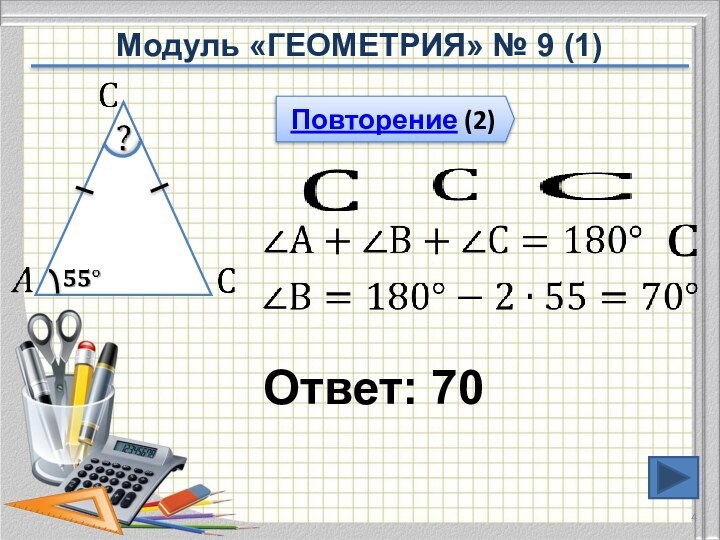
Модуль «ГЕОМЕТРИЯ» № 9 (4)

параллельны.
Если две параллельные прямые пересечены третьей, то сумма внутренних

«ГЕОМЕТРИЯ» № 9 (5)

мера равна сумме градусных мер его частей.
В параллелограмме сумма

.
Найти больший угол.
∠1+∠2=180°
Пусть K – коэффициент пропорциональности,
тогда

3k+7k=180

10k=180

k=18

∠1=18°∙7=126°

Модуль «ГЕОМЕТРИЯ» № 9 (6)

пересечены третьей, то сумма внутренних односторонних углов равна 180°

68°. Найти больший угол.
∠А+∠В=180°
Если ∠А=х°, то ∠В =

х+х+68=180

2х=180-68

х = 56

∠В=56°+68°=124°

∠В=∠С

Модуль «ГЕОМЕТРИЯ» № 9 (7)

прилежащих боковой стороне трапеции равна 180°.

А


5
⇒
⇒
По теореме Пифагора

катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен сумме

А


15
⇒
⇒
По теореме Пифагора

катета к прилежащему
В прямоугольном треугольнике квадрат гипотенузы равен сумме

А

26
BH = HA, значит АВ = 2

H

⇒

HA = СH = 26

АВ = 2 ∙26 = 52

и медианой
В прямоугольном треугольнике сумма острых углов равна 90⁰
Если

H
С
BH=HA, зн. АH=½ AB=
По теореме Пифагора в

и медианой
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов

H
С

120⁰
Проведем высоту CH, получим ∆ВCH.
∠ВCH=60⁰

⇒

∠CВH=30⁰

⇒

По теореме Пифагора в ∆BCH

биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий против угла

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

– биссектриса ∠B, P=10,
АЕ:ЕD=1:3.
Найти: AD



В
А
D
С
Е

1

2

3

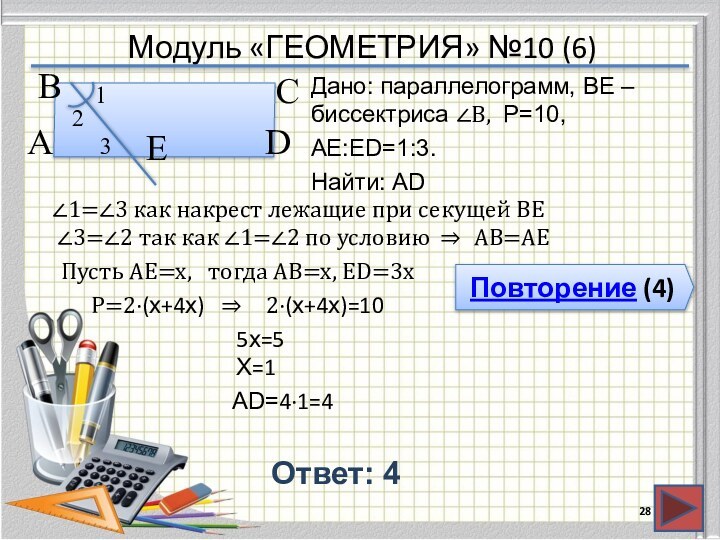
∠1=∠3 как накрест лежащие при секущей ВЕ

∠3=∠2 так как ∠1=∠2 по условию

⇒

АВ=АЕ

Пусть АЕ=х,

тогда АВ=х, ЕD=3х

Р=2∙(х+4х)

⇒

2∙(х+4х)=10

5х=5

Х=1

AD=4∙1=4

многоугольника – это сумма длин всех сторон многоугольника
При пересечении

Если два угла в треугольнике равны, то треугольник - равнобедренный

AH=51, HD=94
Найти среднюю линию трапеции

В
А
D
С
94

51

H

?

К

М

Проведем СЕ⍊AD, получим ∆ABH=∆CED и прямоугольник BCEH

⇒

AD=AH+HE+ЕD=

E

51+94=145

⇒

AH=ЕD=51,

BC=HE=HD-ED=94-51=43,

⇒

равны гипотенузе и катету другого треугольника, то треугольники равны
Если

Средняя линия трапеции равна полусумме оснований трапеции

С
А

8
3
30⁰

синус угла между ними

АВС

В
С
А

3

H
АВ=3CH=3∙3=9

к противоположной стороне под прямым углом
Площадь треугольника равна половине

Найти S∆ABC


В
А
D
С
8
5

угла между ними
Сумма квадратов синуса и косинуса одного и

12 и 7.
Найти площадь ромба.


В
А
D
С

это параллелограмм с равными сторонами

АС=10.
Найти площадь прямоугольника

В
А
D
С

60⁰

О

АО=ВО=10:2=5

В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰

⇒

АВ=5

По теореме Пифагора в ∆АВD

равнобедренном треугольнике углы при основании равны
Если угол разбит на

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Площадь прямоугольника равна произведению соседних сторон

ВС в 2 раза меньше AD. Найти площадь трапеции

В

А

D

С

14

H

ВС=14:2=7

BC=BH=7

– это четырехугольник, две стороны которого параллельны

ABCD – равнобедренная трапеция MK=8, боковая сторона

В

А

D

С

8

135⁰

H

К

М

⇒

По теореме Пифагора в ∆АВH, где AH=BH=х

∠АВH=135⁰-90⁰=45⁰

⇒

∠ВАH= ∠АВH=45⁰

⇒

линия трапеции равна полусумме оснований
Если в прямоугольном треугольнике острый

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

(в градусах)

В
С
А
Проведем из произвольной точки луча

Получим прямоугольный равнобедренный треугольник

⇒

∠С=∠В=45⁰

по свойству острых углов прямоугольного треугольника

прямой угол
В равнобедренном треугольнике углы при основании равны
Сумма острых

(в градусах)

В
С
А

Проведем из произвольной точки

D

Получим прямоугольный равнобедренный треугольник BCD

⇒

∠С=∠В=45⁰

по свойству острых углов прямоугольного треугольника

∠ABС+∠CВD=180⁰ как смежные

⇒

∠ABС=180⁰ - ∠CВD=135⁰

острых углов прямоугольного треугольника равна 90⁰
Смежными углами называются углы,

Сумма смежных углов равна 180⁰

ВАС


В
С
А

4
3

По теореме Пифагора в

противолежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен

ВАС


В
С
А


По теореме Пифагора в ∆АВС

прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен

ВАС.


В
С
А

12
13

По теореме Пифагора в

противолежащего катета к прилежащему
В прямоугольном треугольнике квадрат гипотенузы равен

угла АВС.
В
С
А
Проведем из произвольной точки луча

Получим прямоугольный равнобедренный треугольник

⇒

∠С=∠В=45⁰

по свойству острых углов прямоугольного тр-ка

острых углов прямоугольного треугольника равна 90⁰
Тангенс угла в 45⁰

АВС

В
С
А

Проведем перпендикуляр из такой точки луча

где АВ=3, АС=4, значит по теореме Пифагора ВС=5 (Пифагоров треугольник)

В данном случае единицей измерения стала клетка.

прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен

любые три различные точки плоскости можно провести единственную прямую.

2.Если угол равен 25⁰, то смежный с ним угол равен 155⁰

3.Через любую точку плоскости можно провести не менее одной прямой

да

нет

да

нет

да

нет

точек.
Каким свойством обладают смежные углы?
Сколько прямых можно провести через

Через любые две точки проходит прямая , и притом только одна

Сумма смежных углов равна 180°

Через точку на плоскости можно провести бесконечно много прямых.

угол равен 56⁰, то вертикальный с ним угол равен

2.Существует точка плоскости, через которую можно провести бесконечное количество различных прямых.

3.Через любую точку плоскости можно провести не более двух прямых.

да

нет

да

нет

да

нет

через точку на плоскости?

Вертикальные углы равны
Через точку на плоскости

три различные прямые проходят через одну общую точку.
2.Существует точка

3.Если угол равен 47⁰, то смежный с ним угол равен 133⁰.

да

нет

да

нет

да

нет

плоскости?
Сформулируйте аксиому параллельных прямых.
Сформулируйте свойство смежных углов.

Три прямых на

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Сумма смежных углов равна 180°.

любые две различные точки плоскости можно провести не более

2.Через любые две различные точки плоскости можно провести не менее одной прямой.

3.Если угол равен 54⁰, то вертикальный с ним угол равен 36⁰.

да

нет

да

нет

да

нет

точек на плоскости.
Сформулируйте свойство вертикальных углов
Вертикальные углы равны.

Через любые

любую точку плоскости можно провести прямую.
2.Через любую точку плоскости

3.Существует точка плоскости, через которую можно провести прямую.

да

нет

да

нет

да

нет

плоскости?
Через точку на плоскости можно провести бесконечно много прямых.
Существует

Через любую точку плоскости можно провести прямую.

две параллельные прямые пересечены третьей прямой, то соответственные углы

2.Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 90⁰

3.Если при пересечении двух прямых третьей соответственные углы равны, то прямые перпендикулярны.

да

нет

да

нет

да

нет

две параллельные прямые пересечены третьей прямой, то соответственные углы

Сформулируйте свойство параллельных прямых относительно внутренних односторонних углов.

Если две параллельные прямые пересечены третьей прямой, то сума внутренних односторонних углов равна 180°

при пересечении двух прямых третьей сумма внутренних накрест лежащих

2.Если при пересечении двух прямых третьей соответственные углы равны 75⁰ и 105⁰, то прямые параллельны

3.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые параллельны

да

нет

да

нет

да

нет

лежащих углов.
Сформулируйте признак параллельности двух прямых относительно соответственных углов.
Сформулируйте

Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.