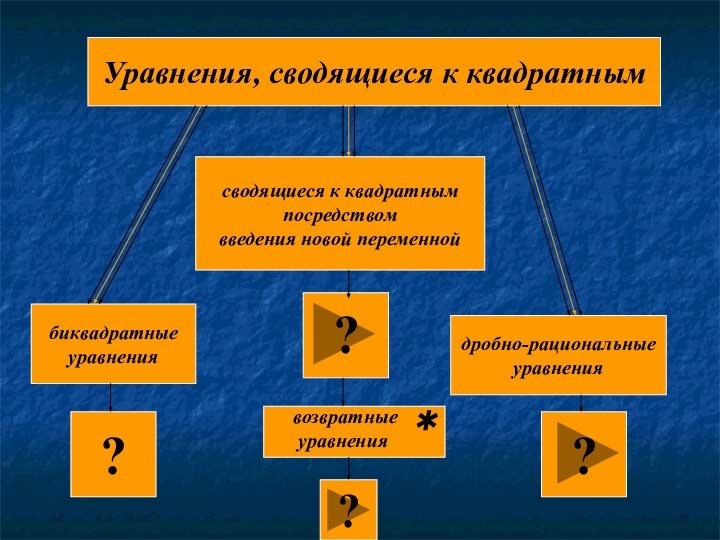
на множители.
- вынесение за скобки общего множителя;
- формулы сокращенного умножения;- способ группировки;
- деление многочлена на многочлен.
2. Приравнять каждый множитель к
нулю. - произведение равно нулю, когда один
из множителей равен нулю, а все
остальные при этом имеют смысл.
3. Решить каждое уравнение отдельно.
4. Записать ответ.