Слайд 2
Нулевой (основной) гипотезой - H0 называют какое-либо конкретное
предположение о теоретической функции распределения или предположение, влекущее за
собой важные практические последствия
Альтернативная гипотеза H1 - любая гипотеза, исключающая нулевую
Слайд 3
Задача проверки статистической гипотезы состоит в том, чтобы,
используя статистические данные (выборку)
X1, X2, …, Xn,
принять
или отклонить нулевую гипотезу
Слайд 4
Нулевые и альтернативные гипотезы формулируются как утверждение о
принадлежности функций распределения некоторой случайной величины определенному классу распределений
Слайд 5
Гипотеза называется простой, если соответствующий класс распределений содержит
лишь одно распределение, в противном случае гипотеза будет сложной.
Гипотезы
о параметрах распределений называются
параметрическими
Слайд 6
значение которой для заданной
выборки служит основанием принятия
или отклонения основной гипотезы
Статистикой критерия
называется функция от выборки
Слайд 7
Статистический критерий - правило, позволяющее только по результатам
наблюдений
X1, X2, …, Xn
принять или отклонить нулевую гипотезу
H0
Слайд 8
Каждому критерию отвечает разбиение области значений статистики критерия
на две непересекающихся части:
критическую область τ1
область принятия
гипотезы τ0
Слайд 9
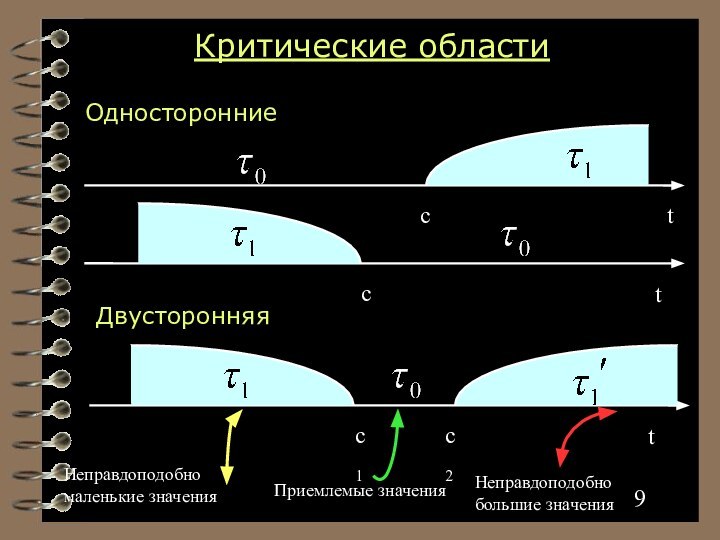
Критические области
Двусторонняя
Неправдоподобно маленькие значения
Неправдоподобно большие значения
Приемлемые значения
Слайд 10
Если значение статистики критерия попадает в область принятия
гипотезы τ0 , то принимается нулевая гипотеза, в противном
случае она отвергается (принимается альтернативная гипотеза)
Слайд 11
Задать статистический критерий значит:
задать статистику критерия
задать критическую область
Слайд 12
В ходе проверки гипотезы H0 можно прийти к
правильному выводу, либо совершить два рода ошибок:
ошибку первого
рода -- отклонить H0, когда она верна
ошибку второго рода -- принять H0, когда она не верна.
Слайд 13
Так как статистика критерия
есть случайная величина со своим
законом распределения, то
попадание её в ту или иную
область характеризуется соответствующими вероятностями:
вероятностью ошибки первого рода α
вероятностью ошибки второго рода β
Слайд 14
Ошибку первого рода α ещё называют уровнем значимости
критерия.
Часто пользуются понятием мощности критерия W -- вероятности попадания
в критическую область при условии справедливости альтернативной гипотезы
Слайд 15
В общем случае вводят функцию мощности
Слайд 16
При разработке статистического критерия невозможно одновременно минимизировать обе
ошибки. Поэтому поступают следующим образом: при заданном числе испытаний
n устанавливается верхняя граница для ошибки первого рода α.
Выбирается тот критерий, у которого наименьшая ошибка второго рода.
Слайд 17
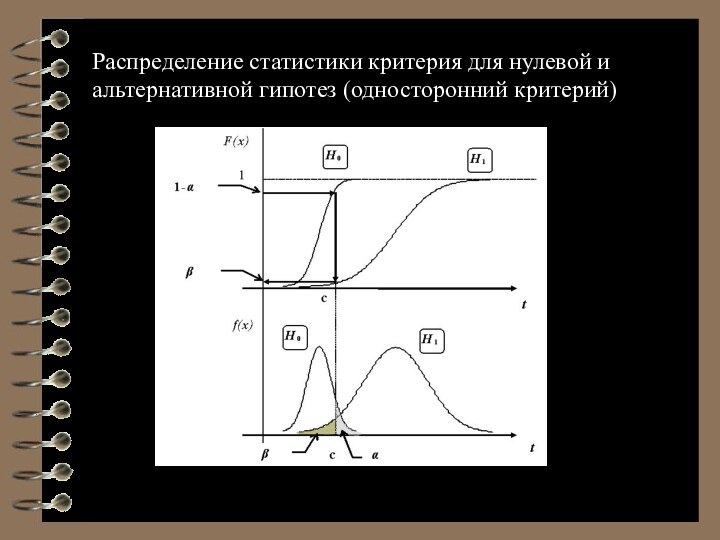
Распределение статистики критерия для нулевой и альтернативной гипотез
(односторонний критерий)
Слайд 18
Уровень значимости α устанавливается из значений следующего ряда:
0.05,
0.01, 0.005, …
события с такими вероятностями считаются практически невозможными.
Допустимая величина уровня значимости определяется теми последствиями, которые наступают после совершения ошибки.
Слайд 19
Примеры формулировок статистических гипотез
Гипотеза о виде распределения:
произведено n
независимых измерений случайной величины с неизвестной функцией распределения F(x).
Следует проверить гипотезу:
Слайд 20
Гипотеза однородности
Произведено k серий независимых испытаний
Можно ли с
достаточной надежностью считать, что закон распределения наблюдений от серии
к серии не менялся? Если это так, то статистические данные однородны.
Проверяется гипотеза однородности:
Слайд 21
Гипотеза независимости
Наблюдается двухмерная случайная величина ξ = (ξ1,
ξ2) с неизвестной функцией распределения Fξ (x, y) и
есть основания полагать, что компоненты
ξ1, ξ2 -- независимы.
В этом случае проверяется гипотеза независимости:
Слайд 22
1 шаг – выдвигается основная гипотеза H0
2 шаг
– задается уровень значимости α
3 шаг – задается статистика
критерия T(X) с известным законом распределения
Пять шагов проверки гипотезы
Слайд 23
4 шаг – из таблиц распределения статистики критерия
находятся квантили, соответствующие границам критической области
5 шаг – для
данной выборки рассчитывается значение статистики критерия
Слайд 24
Если значение статистики критерия попадает в область принятия
гипотезы, то нулевая гипотеза принимается на уровне значимости α.
В
противном случае принимается альтернативная гипотеза (отвергается нулевая гипотеза)
Слайд 25
Среди критериев выделяются такие, которые улавливают любые отклонения
от нулевой гипотезы.
Они называются
« критерии согласия »
Слайд 26
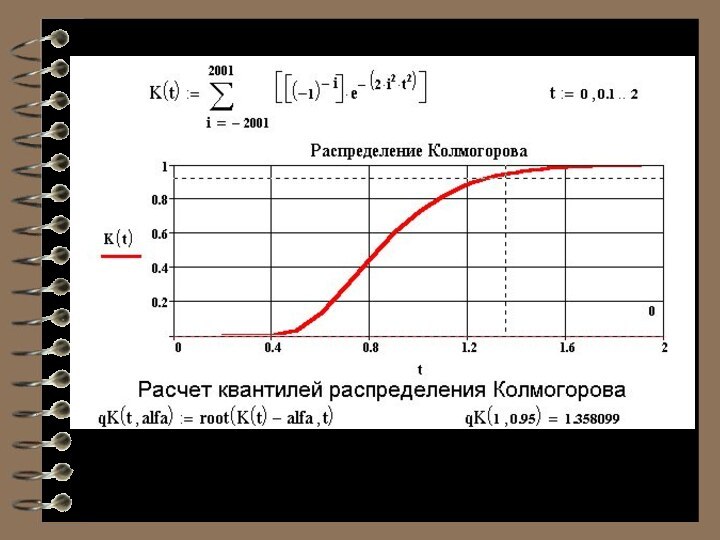
Критерий согласия Колмогорова
Применяется для проверки гипотезы о виде
распределения
При условии, что теоретическая функция распределения непрерывная и полностью
определена
Слайд 27
Критерий согласия Колмогорова
За меру близости распределений принимается максимальное
отклонение эмпирической функции распределения Fn(x) от теоретической F(x).
Слайд 29
Распределение статистики Колмогорова не зависит от F (x).
При больших n оно стремится к распределению Колмогорова.
Статистика
критерия
Слайд 31
Критерий согласия χ2 Пирсона
(хи-квадрат)
Первоначально разработан для дискретных
распределений