Презентация на тему Теорема Пифагора

знаний к решению задач. Обеспечить на уроке условия для

продуктивной, познавательной деятельности при решении задач конструктивного и творческого уровней
Развивающие: Создать условия для развития у учащихся интереса к предмету геометрии и её истории. Содействовать быстрой актуализации и практическому применению полученных знаний, умений и способов действий в нестандартной ситуации.
Воспитательные: Содействовать формированию у учащихся ответственности за свою деятельность. Способствовать формированию у учащихся ответственности за сохранение и укрепление своего здоровья.

Устная работа

Зрительная гимнастика

Тема урока: Теорема Пифагора

Историческая справка

Самостоятельная работа

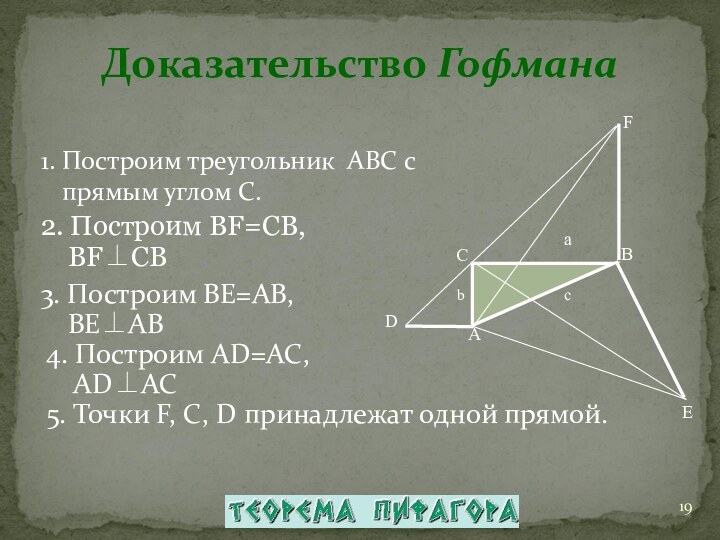
Некоторые способы доказательства теоремы

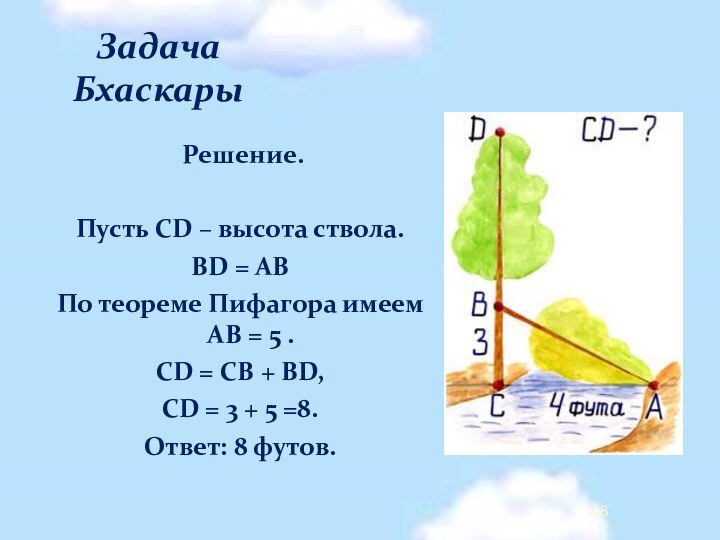
Занимательные задачи

500 до н.э.)

Пифагор родился около 570 г. до

н. э. В молодости он много путешествовал, собирая по крупицам знания древнейших народов по математике, астрономии, технике. Вернувшись на родину, на остров Самос, он собирает вокруг себя юношей и ведёт с ними беседы. Так образовался “ пифагорейский союз”. В союзе царит дисциплина, послушание. Слово учителя закон. Вскоре союз становится политическим союзом единомышленников. Нам чужды политические взгляды Пифагора-аристократа, но исключительные заслуги Пифагора-учёного вызывают у нас уважение и восторг.

меню

Найдите высоту.

E

F

Q

8

6

?

B

A

C

15

15

24

?

h

Ответ: 10

Ответ: 9

Найдите катет.




A
B
C
24
30

60

36
?
Ответ:

12√3 Ответ: 18√3

?

сторону ромба.


13
5
?
A

D

B

C

O

K

A

M

N

?

AM=10см
KN=24см

Ответ: 12 Ответ: 13

меню

I Вариант
1)Катеты 8 и 15 см. Найти гипотенузу
2)Гипотенуза 61

см, катет
11 см. Найти другой катет
3)Диагональ прямоугольника 15 см, одна из сторон – 9 см. Найти его периметр

II Вариант
1)Гипотенуза 37 см, катет 35 см. Найти другой катет.
2)Катеты 7 и 24 см. Найти гипотенузу.
3)Диагональ прямоугольника 17 см, одна из сторон – 15 см. Найти его периметр

4) * Катеты прямоугольного треугольника относятся как
3 : 4, а гипотенуза равна 15 см. Найдите периметр треугольника.

Ответы

225
25х2 = 225
х2 = 9
х = 3
Стороны треугольника 9,

12, 15. Р = 36

Задача 4

меню

Вариант 1
Задача 1
Ответ: 17
Задача 2
Ответ: 60
Задача 3
Ответ: 42

Вариант 2
Задача 1
Ответ: 12
Задача 2
Ответ: 25
Задача 3
Ответ: 46

квадратов, построенных на его катетах.
Доказательство Пифагора

Гофмана
2. Построим BF=CB, BF⊥CB

3. Построим BE=AB, BE⊥AB

4. Построим AD=AC,

AD⊥AC

5. Точки F, C, D принадлежат одной прямой.

равновелики. Треугольники ABF и ЕCB равны. Значит треугольники

ADF и ACE тоже равны.
7. Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим:
1/2а2+1/2b 2=1/2с 2
8. Соответственно:
а2+ b 2 =с 2

a

сопровождало лишь одно слово: СМОТРИ!

стороны равна 0,5ab,
с другой 0,5pr, где

p – полупериметр треугольника,
r – радиус вписанной в него окружности (r=0,5(a+b-c)).

– ac + ab + b2 – bc +

ca + cb - с2)
аb=0,5(а2 + b2- с2 +2ab)/·2
2аb=а2 + b2- с2 +2ab
а2 + b2- с2 =0

3. Отсюда следует, что с2= а2+b2

меню

одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка

над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”

Древнеиндийская задача

Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?

озера АС =Х, тогда AD = AB = Х

+ 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5)2 – Х2 = 22 ,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.

порыв его ствол надломал. Бедный тополь упал. И угол

прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у края реки, осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?

Задача индийского
математика XII в. Бхаскары  

АВ
По теореме Пифагора имеем АВ = 5

.
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.

   Пребудет вечной истина, как скоро    Все познает слабый человек!    И ныне

теорема Пифагора    Верна, как и в его далекий век.
A.Шамиссо

Кадомцев, Э. Г. Позняк, И. И. Юдина 7-9. Учебник

для общеобразоват. учреждений/ - М.,Просвещение,2012.
2. Математика, 5-11 кл. Практикум-1С: Образование 3.0. ЗАО «1С», 2003-2004г. (электронное пособие, раздел Планиметрия→ Исследования и практикумы→ Теорема Пифагора).
3. Г.И.Глейзер История математики в средней школе Просвещение 1970г.
4. Я.И.Перельман Занимательная геометрия Москва «Наука» 1976г
5. Зрительная гимнастика по Базарнову В.Ф.
6. Энциклопедический словарь юного математика /Сост.А. П. Савин. - Педагогика, 1985

Интернет-ресурсы
wikikurgan.orbitel.ru/images/d/d3/Rechkalova_M.G.-prez10.ppt
wwwwww.all-biography.ru
httphttp://http://wwwhttp://www.http://www.zaitsevahttp://www.zaitseva-http://www.zaitseva-irinahttp://www.zaitseva-irina.http://www.zaitseva-irina.ruhttp://www.zaitseva-irina.ru/
wwwwww.wiki.ciit.zp.ua