пересечении
серединных перпендикуляров к сторонам треугольника.
2. Точка
пересечения высот –ортоцентр.
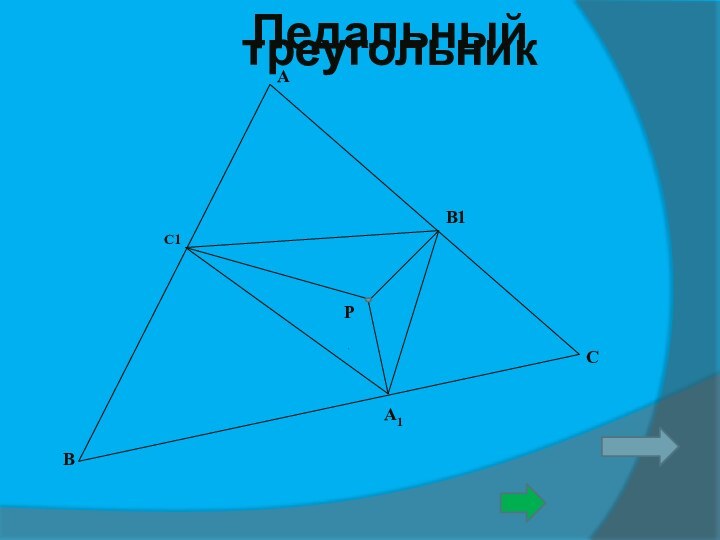
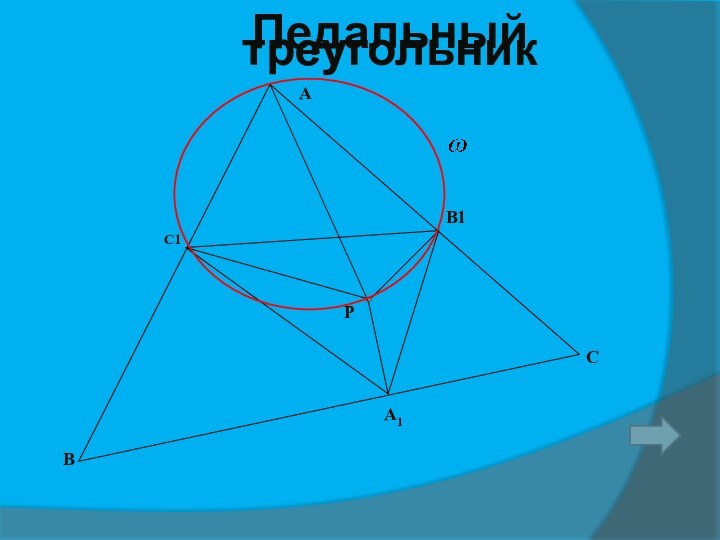
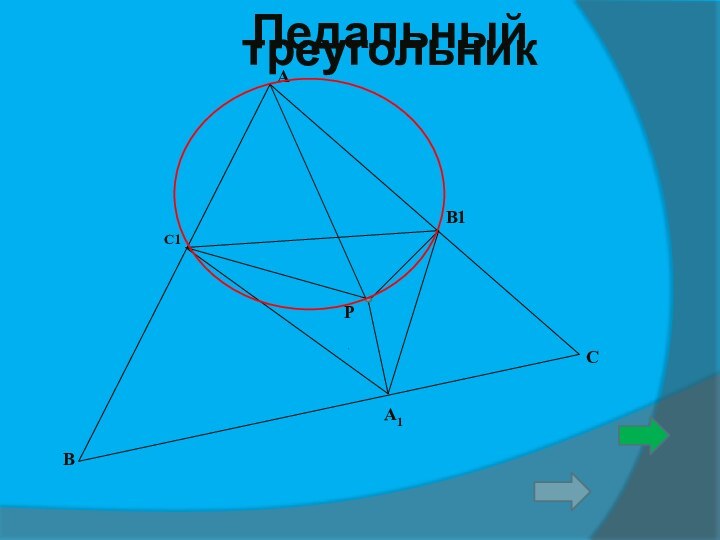
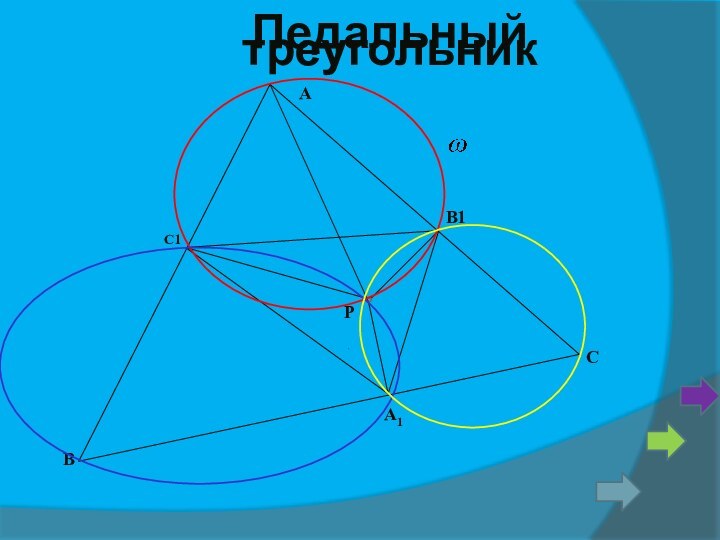
3.Соединяя основания высот треугольника получим-
ортотреугольник.