Презентация на тему Величины и их измерение. (Тема 4)

сравнение (, =) и которым можно поставить в

соответствие некоторую количественную характеристику.

Форма, цвет, материал - не являются величинами, т.к. они не допускают сравнения (например, нельзя сказать «более деревянный» или «менее деревянный».
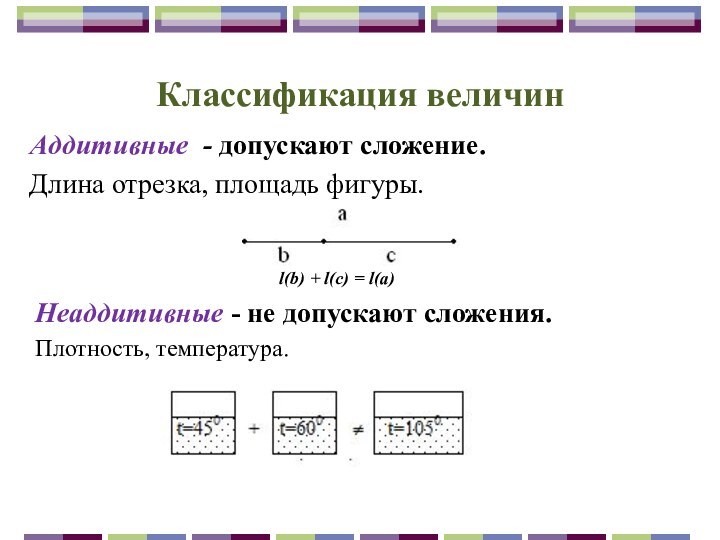
Длина отрезка, площадь фигуры, масса тела - величины.

масса тела, площадь фигуры.
Векторные - определяются числовым значением и

направлением.
Скорость, сила, ускорение.

Длина отрезка, площадь фигуры.
 

l(b) + l(c) = l(a)
Неаддитивные - не допускают сложения.
Плотность, температура.

объектов.
Длина отрезка и периметр треугольника.
Неоднородные - выражают различные свойства

объектов.
Периметр треугольника и площадь треугольника.

В дальнейшем будем рассматривать множество положительных скалярных аддитивных величин V+.

однородные скалярные величины можно сравнить. Если α и β

- однородные положительные скалярные величины, то для них справедливо одно из трех утверждений:
1) α = β или 2) α < β или 3) α > β.




l(a) = l(b) l(a) < l(b) l(a) > l(b)
 

 

скалярные величины можно складывать. В результате получится величина того

же рода.


l(b) + l(c) = l(a)

Аксиома 3: Из большей положительной скалярной величины можно вычесть меньшую положительную скалярную величину, ей однородную. В результате получится величина того же рода.
l(a) – l(b) = l(c) l(a) – l(с) = l(b)

величину можно умножить на положительное действительное число. В результате

получится величина того же рода.




l(a) ⋅ 4 = l(c)

величину можно разделить на величину, ей однородную. В результате

получится положительное действительное число.




l(c) : l(a) = 4

в соответствие количественную характеристику - численное значение (меру) при

выбранной единице измерения. Отыскать численное значение величины возможно в результате ее измерения.
Измерение положительных скалярных величин - это процесс установления отображения из множества положительных скалярных величин V+ во множество положительных действительных чисел R+.

каждого множества измеряемых объектов, но при этом имеются следующие

общие моменты:
1. В каждом множестве измеряемых объектов выбирается один и называется единичным.
2. Величине единичного объекта ставится в соответствие положительное действительное число 1.
3. Величина измеряемого объекта делится на величину единичного объекта.
В результате (по аксиоме 5 положительных скалярных величин) получится положительное действительное число – численное значение (мера) величины измеряемого объекта при выбранной единице измерения.
mе(a) - мера величины а при единице измерения е.

mе(e) = 1 - свойство меры единичного объекта.
2. (а=b)=>(mе(a)=mе(b))

- свойство инвариантности меры. Равным величинам соответствуют равные положительные действительные числа.
3. (с=a ⊕ b)=>(mе(c)=mе(a)+mе(b)) - свойство аддитивности меры.
4. mе(а) = mе1(а) ⋅ mе(е1) - свойство мультипликативности меры (позволяет переходить от одних единиц измерения к другим).