Слайд 2
Задания №15
базового уровня
(прямоугольник)
Слайд 3
Содержание
Задача №1
Задача №2
Задача №3
Задача
№4
Задача №5
Задача №6
Задача №7
Задача №8
Задача
№9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
Задача №22
Задача №23
Задача №24
Задача №25
Задача №26
Задача №27
Задачи для самостоятельного решения
Слайд 4
Задача №1
Найдите площадь прямоугольника, вершины которого имеют координаты
(1;1), (10;1), (10;7), (1;7).
Слайд 5
Задача №2
Найдите площадь квадрата, если его диагональ
равна 1.
Площадь квадрата равна половине произведения его диагоналей.
Поэтому она равна 0,5.
Слайд 6
Задача №3
Найдите диагональ квадрата, если его площадь равна
2.
Площадь квадрата равна половине произведения его диагоналей. Поэтому произведение
диагоналей равно 4, а каждая из них равна 2.
Слайд 7
Задача №4
Найдите сторону квадрата, площадь которого равна площади
прямоугольника со сторонами 4 и 9.
Поэтому сторона квадрата, площадь
которого равна 36, равна 6.
Слайд 8
Задача №5
Найдите площадь прямоугольника, если его периметр равен
18, и одна сторона на 3 больше другой.
Пусть
одна из сторон прямоугольника
равна a, тогда вторая равна a+3.
P = 2a + 2(a + 3) = 18; 2а+2а +6=18; 4а=12; а=3
S = 3 · 6 = 18.
Слайд 9
Задача №6
Найдите
площадь прямоугольника, если его периметр равен 18, а отношение
соседних сторон равно 1:2.
Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a.
Периметр будет соответственно равен P = 2a + 2; 2a = 18, тогда одна из сторон равна 3, а другая 6. Поэтому S = 3 ·6 = 18.
Слайд 10
Задача №7
Найдите периметр прямоугольника, если его площадь равна
18, а отношение соседних сторон равно 1:2.
Пусть одна
из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника будет равна S = 2a2 = 18, тогда одна из сторон равна 3, а другая 6. Поэтому P = 2 ·3 + 2·6 = 18.
Слайд 11
Задача №8
Периметр прямоугольника равен 42, а площадь 98.
Найдите большую сторону прямоугольника.
Пусть одна из сторон прямоугольника
равна a, вторая равна b. Площадь и периметр прямоугольника будут соответственно равны S = a·b = 98, P = 2·a + 2·b = 42. Решая систему из этих уравнений, получаем, что a1 = 7, a2 = 14, b1 = 14, b2 = 7. Значит большая сторона равна 14.
Слайд 12
Задача №9
Периметр прямоугольника равен 34, а площадь
равна 60. Найдите диагональ этого прямоугольника.
Диагональ разбивает прямоугольник
на два прямоугольных треугольника, в которых она является гипотенузой. Пусть длина диагонали равна с, тогда по теореме Пифагора
Слайд 13
Задача №10
Сторона прямоугольника относится к его диагонали,
как 4:5, а другая сторона равна 6. Найдите площадь
прямоугольника.
Пусть одна из сторон прямоугольника равна 4a, тогда диагональ равна 5a. Диагональ образует в прямоугольнике два прямоугольных треугольника. По теореме Пифагора 16a2 + 36 = 25a2, тогда 9a2 = 36, откуда a = 2. Значит S = 8·6 = 48.
Слайд 14
Задача №11
Даны два квадрата, диагонали которых равны 10
и 6. Найдите диагональ квадрата, площадь которого равна разности
площадей данных квадратов.
Площадь квадрата равна половине квадрата его диагонали. Поэтому площадь первого квадрата равна 50, а площадь второго квадрата равна 18. Разность найденных площадей равна 32, значит, квадрат искомой диагонали равен 64, а сама она равна 8.
Слайд 15
Задача №12
Во сколько раз площадь квадрата, описанного около
окружности, больше площади квадрата, вписанного в эту окружность?
Пусть
радиус окружности равен R. Тогда сторона описанного вокруг нее квадрата равна 2R, а его площадь, равная квадрату стороны, равна 4R². Диагональ вписанного квадрата также равна 2R, поэтому его площадь, равная половине произведения диагоналей, равна 2R². Значит, отношение площади описанного квадрата к площади вписанного равно 2.
Слайд 16
Задача №13
Две стороны прямоугольника АВСD равны 6 и 8.
Найдите длину вектора АС .
Вектор АС образует в прямоугольнике
два прямоугольных
треугольника.
Поэтому по теореме Пифагора
Слайд 17
Задача № 14
Две стороны прямоугольника АВСD равны 6 и
8. Найдите сумму векторов АВ и АD.
Сумма векторов АВ и
АD равна вектору АС.
Вектор АС образует в прямоугольнике два
прямоугольных треугольника.
Поэтому по теореме Пифагора
Слайд 18
Задача №15
Две стороны прямоугольника АВСD равны 6 и 8.
Найдите разность векторов
Разность векторов АВ и АD равна вектору DВ.
Вектор
DВ образует в прямоугольнике два
прямоугольных треугольника.
Поэтому
Слайд 19
Задача №16
Две стороны прямоугольника АВСD равны 6 и 8.
Найдите скалярное произведение векторов АВ и АD.
Скалярное произведение двух
векторов равно произведению их длин на косинус угла между ними. Так как косинус прямого угла равен нулю, то и скалярное произведение тоже равно нулю.
Слайд 20
Задача №17
Две стороны прямоугольника АВСD равны 6 и 8.
Диагонали пересекаются в точке О. Найдите длину суммы векторов АО
и ВО.
Сумма векторов АО и ВО равна вектору
АD. Значит его длина равна 6.
Слайд 21
Задача №18
Две стороны прямоугольника АВСD равны 6 и 8.
Диагонали пересекаются в точке О. Найдите длину разности векторов АО
и ВО.
Разность векторов АО и ВО равна вектору АВ. Значит длина вектора равна 8 .
Слайд 22
Задача №19
Найдите диагональ прямоугольника, если его периметр равен
28, а периметр одного из треугольников, на которые диагональ
разделила прямоугольник, равен 24.
Сумма двух периметров треугольников отличается от периметра прямоугольника на две длины диагонали, значит
Слайд 23
Задача №20
Середины сторон прямоугольника, диагональ которого равна 5,
последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Четырехугольник EHGF ромб,
значит, его периметр равен 4·EF. Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Значит стороны искомого четырехугольника равны половинам диагоналей. Значит, имеем:
Слайд 24
Задача №21
В прямоугольнике расстояние от точки пересечения
диагоналей до меньшей стороны на 1 больше, чем расстояние
от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.
=>
Слайд 25
Задача №22
Найдите периметр четырехугольника АВСD, если стороны квадратных клеток
равны √10.
по теореме Пифагора найдем сторону
четырехугольника:
Слайд 26
Задача №23
Меньшая сторона прямоугольника равна 6, диагонали пересекаются
под углом 60°. Найдите диагонали прямоугольника.
значит, треугольник DОА –
равносторонний.
Слайд 27
Задача №24
Диагональ прямоугольника вдвое больше одной из его
сторон. Найдите больший из углов, который образует диагональ со
сторонами прямоугольника? Ответ выразите в градусах.
Диагональ прямоугольника является гипотенузой прямоугольного треугольника. Так как она вдвое больше одной из сторон прямоугольника, являющейся катетом того же треугольника, то угол, лежащий против этой стороны, равен 30°. Больший угол будет равен 90° - 30° = 60°
Слайд 28
Задача №25
В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 6.
Найдите диагональ данного прямоугольника.
Т.к. диагональ делит угол в отношении 1 : 2, значит, углы
равны 30°и 60°. Диагональ тогда равна удвоенной длине
катета, лежащего против угла в 30°, то есть 12.
Слайд 29
Задача №26
Найдите сторону квадрата, диагональ которого равна √8 .
Слайд 30
Задача №27
В квадрате расстояние от точки пересечения диагоналей
до одной из его сторон равно 7. Найдите периметр
этого квадрата.
В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а тогда его периметр 56.
Слайд 31
Задачи
для самостоятельного решения
Слайд 32
Задача №1 Решите самостоятельно
Найдите площадь прямоугольника, вершины которого
имеют координаты (1;2), (10;2), (10;7), (1;7). Ответ:
2) Найдите
площадь прямоугольника, вершины которого имеют координаты (2;2), (10;2), (10;9), (2;9) . Ответ:
3) Найдите площадь прямоугольника, вершины которого имеют координаты (4;1), (10;1), (10;8), (4;8) . Ответ:
Слайд 33
Задача №2 Решите самостоятельно
1) Найдите площадь квадрата, если
его диагональ равна 38. Ответ:
722
2) Найдите площадь квадрата, если его диагональ равна 30. Ответ:
3) Найдите площадь квадрата, если его диагональ равна 16. Ответ:
Слайд 34
Задача №5 Решите самостоятельно
Найдите площадь прямоугольника, если его
периметр равен 80, и одна сторона на 6 больше
другой. Ответ:
2) Найдите площадь прямоугольника, если его периметр равен 12, и одна сторона на 2 больше другой. Ответ:
3) Найдите площадь прямоугольника, если его периметр равен 88, и одна сторона на 6 больше другой. Ответ:
Слайд 35
Задача №6 Решить самостоятельно
Найдите площадь прямоугольника, если
его периметр равен 140, а отношение соседних сторон равно
4:31.
Ответ:496
2) Найдите площадь прямоугольника, если его периметр равен 126, а отношение соседних сторон равно 2:19.
3) Найдите площадь прямоугольника, если его периметр равен 64, а отношение соседних сторон равно 3:13.
Слайд 36
Задача №7 Решить самостоятельно
Найдите периметр прямоугольника, если его
площадь равна 176, а отношение соседних сторон равно 4:11.
Ответ:60
2) Найдите периметр прямоугольника, если его площадь равна 272, а отношение соседних сторон равно 4:17.
3) Найдите периметр прямоугольника, если его площадь равна 432, а отношение соседних сторон равно 4:27.
Слайд 37
Задача №8 Решить самостоятельно
Периметр прямоугольника равен 42, а
площадь 108. Найдите большую сторону прямоугольника. Ответ:
2) Периметр прямоугольника
равен 90, а площадь 234. Найдите большую сторону прямоугольника. Ответ:
3) Периметр прямоугольника равен 30, а площадь 36. Найдите большую сторону прямоугольника. Ответ:
Слайд 38
Задача №10 Решить самостоятельно
Сторона прямоугольника относится к его
диагонали, как 12:13, а другая сторона равна 35. Найдите
площадь прямоугольника. Ответ:
2) Сторона прямоугольника относится к его диагонали, как 21:29, а другая сторона равна 80. Найдите площадь прямоугольника. Ответ:
3) Сторона прямоугольника относится к его диагонали, как 15:17, а другая сторона равна 48. Найдите площадь прямоугольника. Ответ:
Слайд 39
Задача №11 Решить самостоятельно
1) Даны два квадрата, диагонали
которых равны 196 и 261. Найдите диагональ квадрата, площадь
которого равна разности площадей данных квадратов.
2) Даны два квадрата, диагонали которых равны 72 и 75. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
3) Даны два квадрата, диагонали которых равны 192 и 200. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Слайд 40
Задача №19 Решить самостоятельно
1) Найдите диагональ прямоугольника, если
его периметр равен 42, а периметр одного из треугольников,
на которые диагональ разделила прямоугольник, равен 37.
2) Найдите диагональ прямоугольника, если его периметр равен 100, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 87.
Слайд 41
Задача №20 Решить самостоятельно
Середины сторон прямоугольника, диагональ которого
равна 24, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Ответ: 48
Середины сторон прямоугольника, диагональ которого равна 46, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Слайд 42
Задача №21 Решить самостоятельно
В прямоугольнике расстояние от точки
пересечения диагоналей до меньшей стороны на 2 больше, чем
расстояние от нее до большей стороны. Периметр прямоугольника равен 52. Найдите меньшую сторону прямоугольника.
В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 3 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 124. Найдите меньшую сторону прямоугольника.
Слайд 43
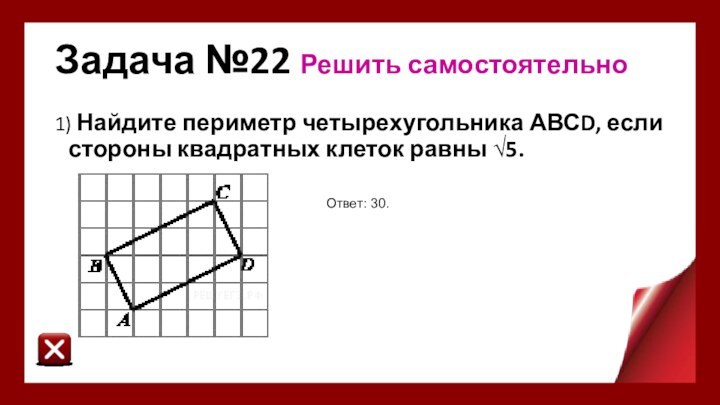
Задача №22 Решить самостоятельно
1) Найдите периметр четырехугольника АВСD, если
стороны квадратных клеток равны √5.
Ответ: 30.
Слайд 44
Задача №23 Решить самостоятельно
Меньшая сторона прямоугольника равна 59,
диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
2)
Меньшая сторона прямоугольника равна 1, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
3) Меньшая сторона прямоугольника равна18, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
Слайд 45
Задача №25 Решить самостоятельно
1) В прямоугольнике диагональ делит
угол в отношении
1 : 2 , меньшая его сторона
равна 57. Найдите диагональ данного прямоугольника.
2) В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 39. Найдите диагональ данного прямоугольника.
3) В прямоугольнике диагональ делит угол в отношении
1 : 2 , меньшая его сторона равна 23. Найдите диагональ данного прямоугольника.
Слайд 46
Задача №26Решите самостоятельно
Найдите сторону квадрата, диагональ которого равна 5√2
. Ответ:
5
Найдите сторону квадрата, диагональ которого равна 14√2 .
Найдите сторону квадрата, диагональ которого равна 9√2 .