- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Связь явлений и их межфакторное взаимодействие в медицине. Корреляционный анализ. Динамические ряды
Содержание
- 2. Общая цель: овладеть навыком трактовки информации о связи явлений в медицине;Лекция 5
- 3. План лекции:1. Оценка взаимосвязи между качественными показателями.2. Оценка взаимосвязи между качественными показателями.Лекция 5
- 4. Наиболее известное когортное исследование, по результатам кото-рого
- 5. В качестве исходов приняли общую смертность (смерть
- 6. Таким образом, исследователи показали, что взаимосвязь между
- 7. Курильщики чаще подвержены инсультам, чем некурящие. Смерть,
- 11. На этом рисунке показана динамика уровня смертности
- 12. Оценка эффектов вмешательства Риск события в контрольной
- 13. Эффект лечения при коронарной болезни При обычном
- 14. Окончательный способ выражения эффекта лечения, это отношение
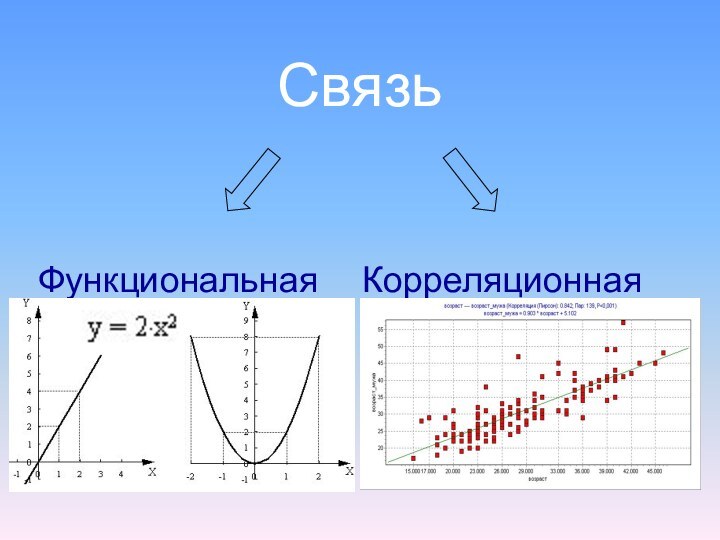
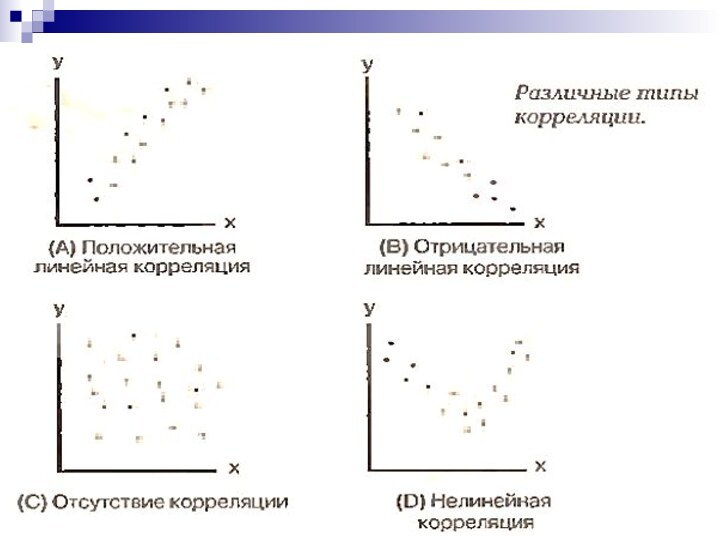
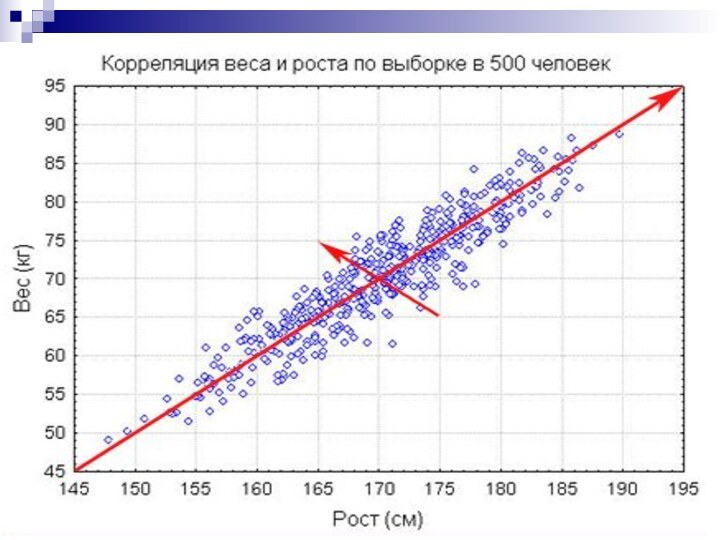
- 15. СвязьФункциональная Корреляционная
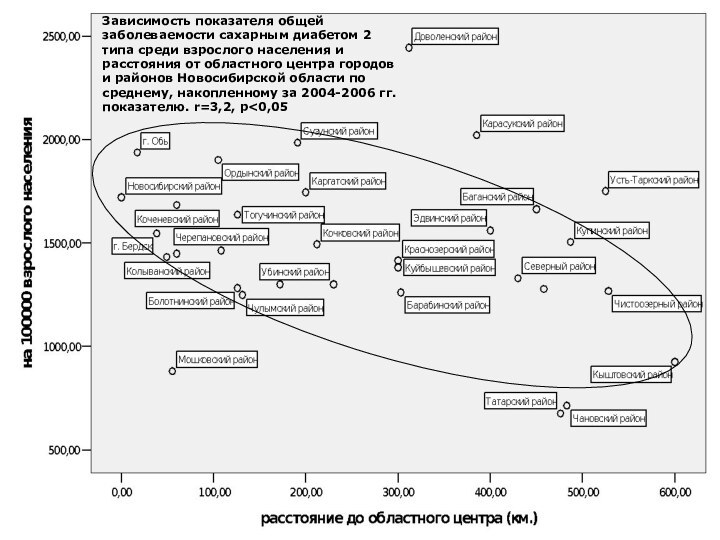
- 19. Зависимость показателя общей заболеваемости сахарным диабетом 2
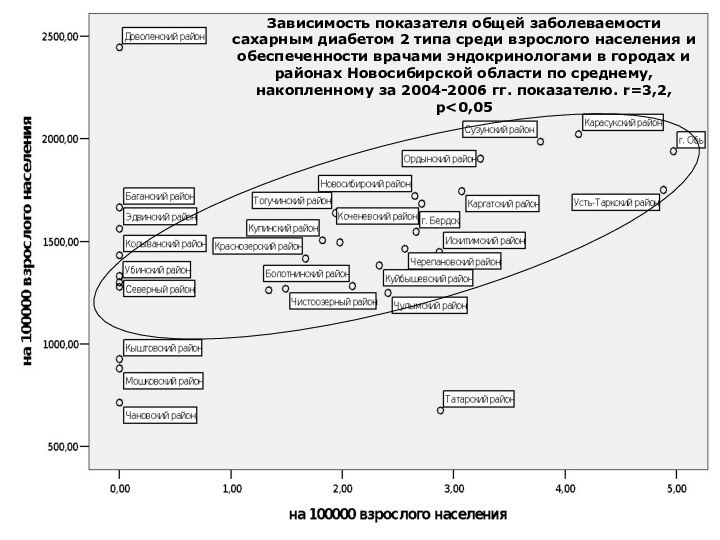
- 20. Зависимость показателя общей заболеваемости сахарным диабетом 2
- 22. Корреляционный коэффициент Пирсона
- 23. Свойства коэффициента корреляции1. Коэффициент корреляции изменяется в интервале от -1 до +1;
- 24. Свойства коэффициента корреляцииПоложительнаяОтрицательная2. По направленности связь может быть прямой (положительной) и обратной (отрицательной):
- 25. Свойства коэффициента корреляцииЕсли r = ±1, то
- 26. Свойства коэффициента корреляции4. Коэффициент корреляции безразмерен, то
- 27. Свойства коэффициента корреляции5. x и y могут
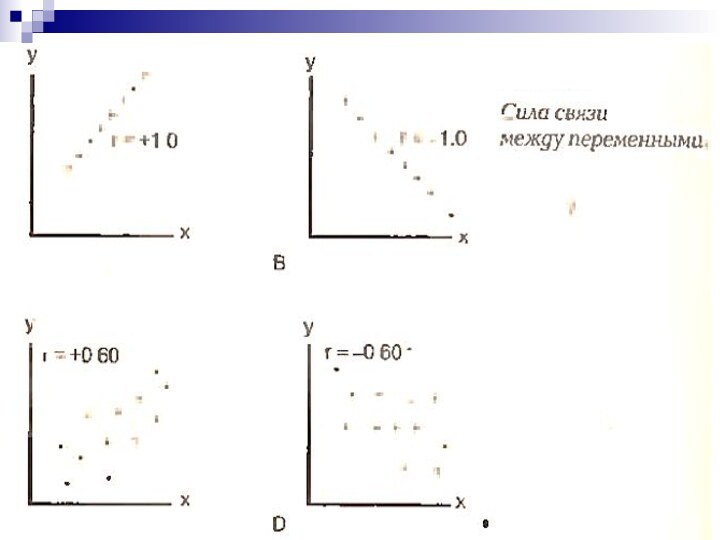
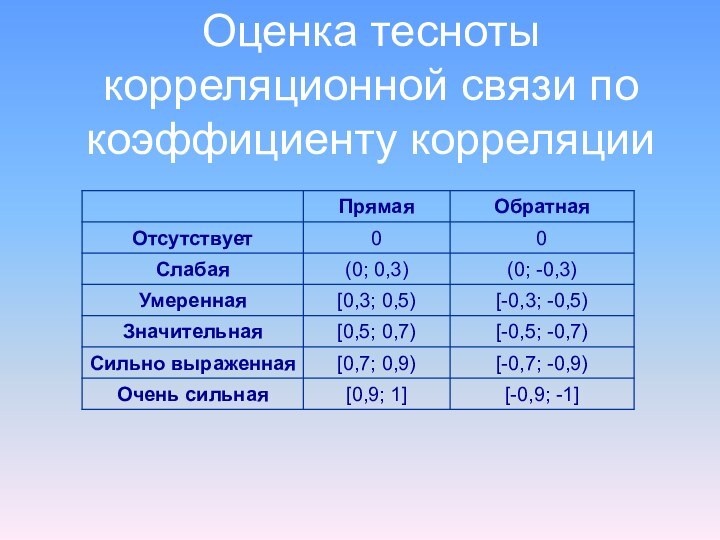
- 28. Оценка тесноты корреляционной связи по коэффициенту корреляции
- 29. Когда не следует раccчитывать r:1. Соотношение между
- 30. Когда не следует раccчитывать r:3. Есть аномальные значения;
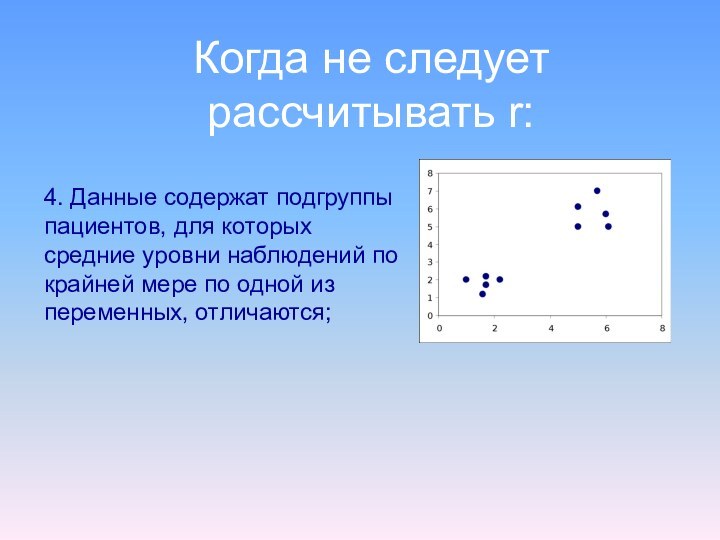
- 31. Когда не следует раccчитывать r:4. Данные содержат
- 32. Средняя ошибка коэффициента корреляцииПри n > 100:При
- 33. Коэффициент ранговой корреляции Спирмена
- 34. Коэффициент ранговой корреляции Спирмена вычисляют когда:Изучаемое явление
- 35. Регрессио́нный (линейный) анализ — статистический метод — статистический метод
- 36. Цели регрессионного анализаОпределение степени детерминированностиОпределение степени детерминированности
- 37. Детерминированность (от лат. determinans — определяющий) — определяемость.
- 38. БИОЛОГИЧЕСКИЙ ВОЗРАСТ (БВ) - это показатель уровня
- 39. В России до настоящего времени наиболее широко
- 40. БВм = 58.873 + 0.180 АДс -
- 42. Для мужчин: БВ = 19,455 +
- 43. Методы анализа динамики явлений (анализ динамических или временных рядов).
- 44. Абсолютный прирост (убыль) – характеризует изменение явления в единицу времени.
- 45. Темп роста – показывает соотношение в процентах последующего и предыдущего уровней.
- 46. Темп прироста – показывает на сколько процентов увеличился или уменьшился уровень явления.
- 47. Абсолютное значение 1% прироста – характеризует значение 1% прироста изучаемого явления.
- 48. Коэффициент наглядности – используются для облегчения сравнения
- 49. СОВРЕМЕННЫЕ ПОДХОДЫ К ОЦЕНКЕ ДИНАМИКИ
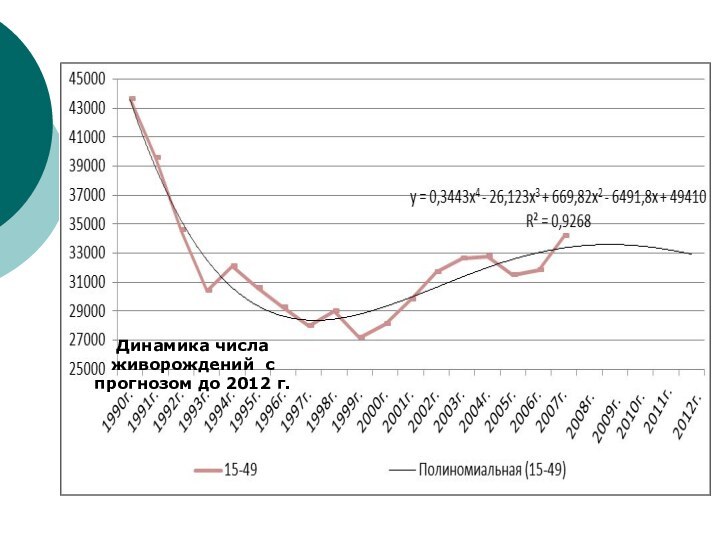
- 51. Прогнозирование процессовГде р — теоретическая вероятность развития
- 52. Выводы:Таким образом мы рассмотрели:Варианты определения взаимосвязи между
- 53. Выводы:- наличие связи;- силу связи: слабая (коэффициент
- 54. Рекомендованная литература по теме занятия:- обязательная; Павлушков
- 55. Скачать презентацию
- 56. Похожие презентации




































Слайд 3
План лекции:
1. Оценка взаимосвязи между качественными показателями.
2. Оценка
взаимосвязи между качественными показателями.
Лекция 5
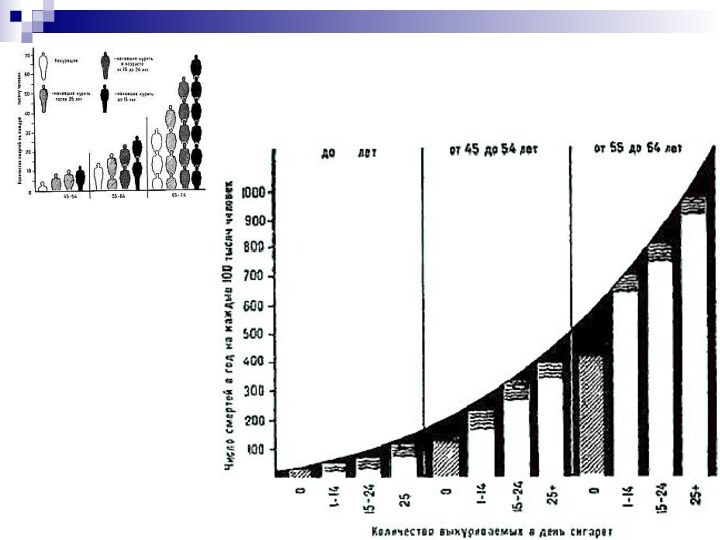
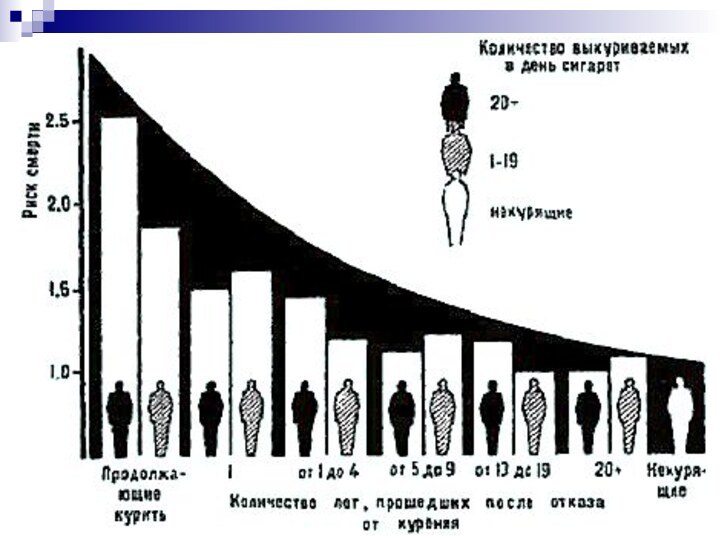
Слайд 4 Наиболее известное когортное исследование, по результатам кото-рого двум
ученым было присвоено рыцарское звание, провели сэр Ос- тен
Брэдфорд Хилл (А.В. Hill), сэр Ричард Долл (R. Doll) и присоединившийся к концу исследования Ричард Пито (R. Peto). Они проводили наблюдение за 40 ООО британских врачей, которых разделили на 4 когорты (некурящие, курящие мало, курящие умеренно и курящие много).Слайд 5 В качестве исходов приняли общую смертность (смерть от
любой причины) и смертность в результате определенного заболевания. Публикация
их 10-летнего исследования в 1964 г. показала существенное увеличение смертности курильщиков как от рака легкого, так и от других причин. Был продемонстрирован «дозо-зависимый» эффект (т.е. чем больше курить, тем выше шансы заболеть раком легких).Слайд 6 Таким образом, исследователи показали, что взаимосвязь между курением
и заболеваемостью скорее закономерна, чем случайна. Результаты через 2052
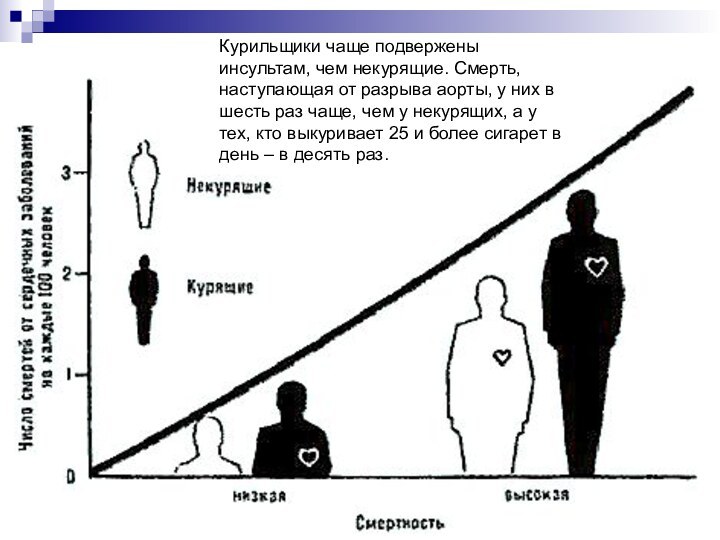
и 40 лет от начала этого важного исследования (с впечатляющей цифрой 94% остававшихся в живых с момента набора в 1951 г.) продемонстрировали роль курения как фактора риска и убедительную силу доказательства, полученного в результате правильно проведенного когортного исследования.Слайд 7 Курильщики чаще подвержены инсультам, чем некурящие. Смерть, наступающая
от разрыва аорты, у них в шесть раз чаще,
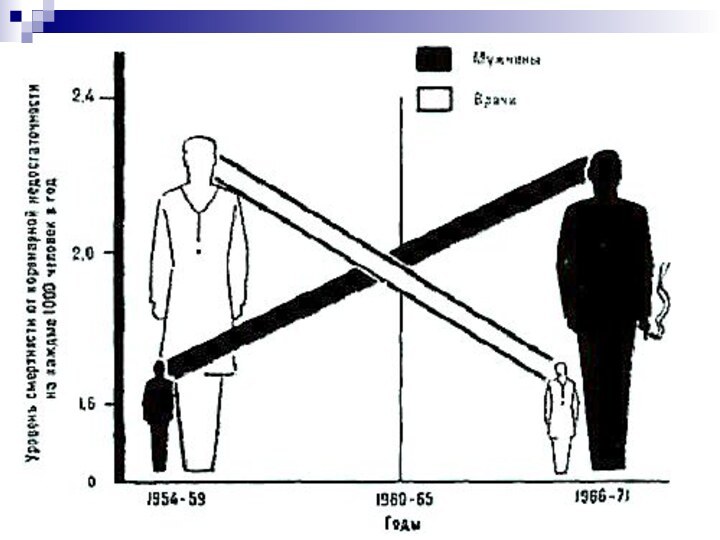
чем у некурящих, а у тех, кто выкуривает 25 и более сигарет в день – в десять раз.Слайд 11 На этом рисунке показана динамика уровня смертности от
коронарной недостаточности у врачей в возрасте до 65 лет
за период с 1954 по 1971 год. До 1954 года смертность среди врачей была выше, чем среди остальных людей, но начиная с 1954 года, когда врачи получили доступ к сведениям о вреде курения и его влиянии на развитие серьезных заболеваний, уровень смертности врачей неуклонно падает. По сравнению с врачами уровень смертности среди прочего населения, напротив, возрастает таким образом, что к 1971 году обе группы наблюдаемых поменялись местами. Это явление может быть объяснено только тем, что врачи, зная о вреде курения и наблюдая своих пациентов, бросили курить, в то время как количество курящих среди прочего населения увеличилось.
Слайд 12
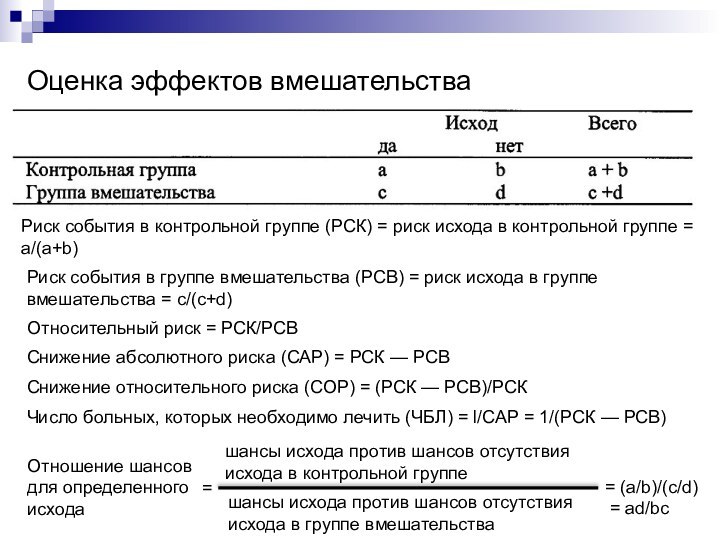
Оценка эффектов вмешательства
Риск события в контрольной группе
(РСК) = риск исхода в контрольной группе = а/(а+b)
Риск события в группе вмешательства (РСВ) = риск исхода в группе вмешательства = c/(c+d)
Относительный риск = РСК/РСВ
Снижение абсолютного риска (САР) = РСК — РСВ
Снижение относительного риска (СОР) = (РСК — РСВ)/РСК
Число больных, которых необходимо лечить (ЧБЛ) = l/САР = 1/(РСК — РСВ)
Отношение шансов для определенного исхода
шансы исхода против шансов отсутствия исхода в контрольной группе
шансы исхода против шансов отсутствия исхода в группе вмешательства
=
= (a/b)/(c/d)
= ad/bc
Слайд 13
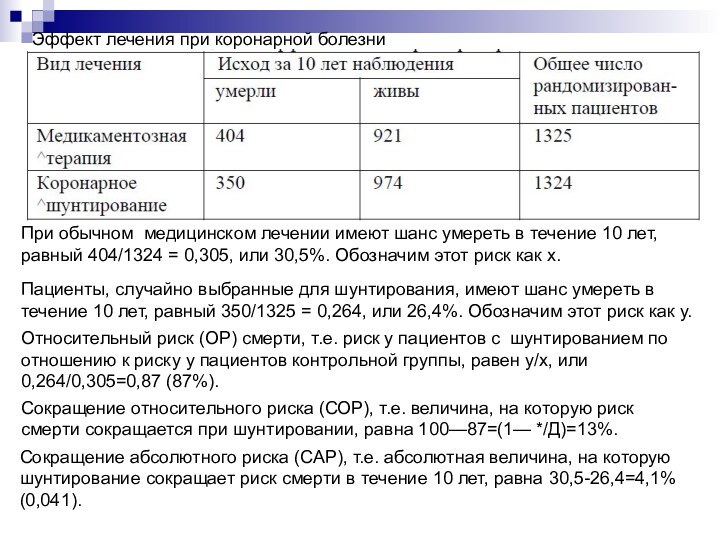
Эффект лечения при коронарной болезни
При обычном медицинском
лечении имеют шанс умереть в течение 10 лет, равный
404/1324 = 0,305, или 30,5%. Обозначим этот риск как х.Пациенты, случайно выбранные для шунтирования, имеют шанс умереть в течение 10 лет, равный 350/1325 = 0,264, или 26,4%. Обозначим этот риск как у.
Относительный риск (ОР) смерти, т.е. риск у пациентов с шунтированием по отношению к риску у пациентов контрольной группы, равен у/х, или 0,264/0,305=0,87 (87%).
Сокращение относительного риска (СОР), т.е. величина, на которую риск смерти сокращается при шунтировании, равна 100—87=(1— */Д)=13%.
Сокращение абсолютного риска (САР), т.е. абсолютная величина, на которую шунтирование сокращает риск смерти в течение 10 лет, равна 30,5-26,4=4,1% (0,041).
Слайд 14 Окончательный способ выражения эффекта лечения, это отношение шансов
(ОШ).
Шансы умереть по сравнению с шансами выжить для
пациентов в группе лечения равны 404/921 = 0,44, а для пациентов в группе шунтирования равны 350/974 = 0,36. Отношение этих шансов будет 0,36/0,44 = 0,82.
Слайд 19
Зависимость показателя общей заболеваемости сахарным диабетом 2 типа
среди взрослого населения и расстояния от областного центра городов
и районов Новосибирской области по среднему, накопленному за 2004-2006 гг. показателю. r=3,2, p<0,05
Слайд 20
Зависимость показателя общей заболеваемости сахарным диабетом 2 типа
среди взрослого населения и обеспеченности врачами эндокринологами в городах
и районах Новосибирской области по среднему, накопленному за 2004-2006 гг. показателю. r=3,2, p<0,05
Слайд 23
Свойства коэффициента корреляции
1. Коэффициент корреляции изменяется в интервале
от -1 до +1;
Слайд 24
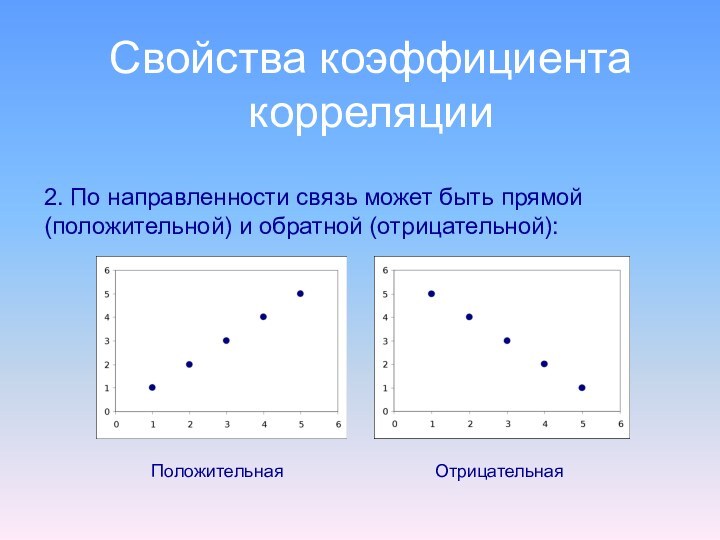
Свойства коэффициента корреляции
Положительная
Отрицательная
2. По направленности связь может быть
прямой (положительной) и обратной (отрицательной):
Слайд 25
Свойства коэффициента корреляции
Если r = ±1, то связь
полная (функциональная).
Если r = 0, то линейной связи нет.
3.
Его величина указывает, как близко расположены точки к прямой линии.
Слайд 26
Свойства коэффициента корреляции
4. Коэффициент корреляции безразмерен, то есть
не имеет единиц измерения. Его величина обоснована только в диапазоне
значений x и y в выборке.
Слайд 27
Свойства коэффициента корреляции
5. x и y могут взаимозаменяться,
не влияя на величину r;
Корреляция между x и y
не обязательно означает соотношение причины и следствия.
Слайд 29
Когда не следует раccчитывать r:
1. Соотношение между двумя
переменными нелинейное;
2. Данные включают более одного наблюдения по каждому
пациенту;
Слайд 31
Когда не следует раccчитывать r:
4. Данные содержат подгруппы
пациентов, для которых средние уровни наблюдений по крайней мере
по одной из переменных, отличаются;
Слайд 32
Средняя ошибка коэффициента корреляции
При n > 100:
При 100
≥ n > 30:
Коэффициент корреляции достоверен если он больше
или равен величине трёх своих ошибок:
Слайд 34
Коэффициент ранговой корреляции Спирмена вычисляют когда:
Изучаемое явление отличается
от нормального распределения;
Требуется измерение связи между двумя переменными, когда
их соотношение нелинейное;Размер выборки небольшой (n<30);
Переменные x и y измеряются в ранговой (порядковой) шкале;
Можно применять как количественным, так и к порядковым признакам.
Слайд 35 Регрессио́нный (линейный) анализ — статистический метод — статистический метод исследования
зависимости между зависимой переменной Y и одной или несколькими
независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
Слайд 36
Цели регрессионного анализа
Определение степени детерминированностиОпределение степени детерминированности вариацииОпределение
степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
Предсказание
значения зависимой переменной с помощью независимой(-ых)Определение вклада отдельных независимых переменных в вариацию зависимой
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
Слайд 37 Детерминированность (от лат. determinans — определяющий) — определяемость. Детерминированность
может подразумевать определяемость на общегносеологическом) — определяемость. Детерминированность может
подразумевать определяемость на общегносеологическом уровне или для конкретного алгоритма. Под детерминированностью процессов в мире понимается однозначная предопределённость.Слайд 38 БИОЛОГИЧЕСКИЙ ВОЗРАСТ (БВ) - это показатель уровня износа
структуры и функции определенного элемента организма, группы элементов и
организма в целом, выраженный в единицах времени путем соотнесения значений замеренных индивидуальных биомаркеров с эталонными среднепопуляционными кривыми зависимостей изменений этих биомаркеров от календарного возраста.Календарный возраст (КВ)
Слайд 39 В России до настоящего времени наиболее широко применяется
так называемая "киевская" методика определения БВ [1], которая представляет
собой типичную линейную регрессионную модель БВ и включает следующий набор показателей: 1. Систолическое, диастолическое и пульсовое артериальное давление (АДс, АДд и АДп) в мм рт.ст.. 2. Скорость распространения пульсовой волны по сосудам эластического типа (СПВэ) на участке сонная - бедренная артерии в м/сек. 3. Скорость распространения пульсовой волны по сосудам мышечного типа (СПВм) на участке сонная - лучевая артерии в м/сек. 4. Жизненная емкость легких (ЖЕЛ) в мл. 5. Время задержки дыхания (ЗД) на выдохе в сек. 6. Аккомодация хрусталика по расстоянию ближней точки зрения (А) в диоптриях. 7. Слуховой порог (СП) при 4000 Гц в Дб. 8. Статическая балансировка (СБ) на левой ноге в сек. 9. Масса тела (МТ) в кг. 10. Самооценка здоровья (СОЗ) - количество неблагоприятных ответов на 29 вопросов стандартной анкеты. 11. Символьно-цифровой тест Векслера (ТВ) - число правильно заполненных ячеек за 90 сек.Слайд 40 БВм = 58.873 + 0.180 АДс - 0.073
АДд - 0.141 АДп - 0.262 СПВэ + 0.646
СПВм - 0.001 ЖЕЛ + 0.005 ЗД - 1.881 А + 0.189 СП - 0.026 СБ - 0.107 МТ + 0.320 СОЗ - 0.327 ТВ (3)БВж = 16.271 + 0.280 АДс - 0.193 АДд - 0.105 АДп + 0.125 СПВэ + 1.202 СПВм - 0.003 ЖЕЛ - 0.065 ЗД - 0.621 А + 0.277 СП - 0.070 СБ + 0.207 МТ + 0.039 СОЗ - 0.152 ТВ (4)
Слайд 42 Для мужчин: БВ = 19,455 + 5,460 СПВэ
- 0,005 ЖЕЛ - 0,052 СБ + 0.166 ЗД
(6)Для женщин: БВ = 1,717 + 5.197 СПВэ- 0,072 СБ + 0,165 СП + 0,017 А (7)
Слайд 48 Коэффициент наглядности – используются для облегчения сравнения и
повышения наглядности. Не изменяя по существу отношения между числами,
они дают более отчетливое представление о характере изменения явления во времени. Выражаются коэффициенты наглядности в процентах или долях единицы, которые вычисляют от исходного уровня, принимаемого за 100%.
Слайд 51
Прогнозирование процессов
Где р — теоретическая вероятность развития несостоятельности
культи бронха (зави-
симая переменная), х — значение суммарного балла
у конкретного больногоДинамика числа живорождений с прогнозом до 2012 г.
Слайд 52
Выводы:
Таким образом мы рассмотрели:
Варианты определения взаимосвязи между количественными
и качественными критериями, а так же анализ динамических рядов.
Слайд 53
Выводы:
- наличие связи;
- силу связи: слабая (коэффициент корреляции
до 0.29), средняя (0.3 - 0.69), сильная (0.7 и
выше);- направление связи: прямая (изменения признаков происходят в одном направлении) и
обратная (изменения признаков происходят в разных направлениях);
Слайд 54
Рекомендованная литература по теме занятия:
- обязательная;
Павлушков И.В.
Основы высшей математики и математической статистики: Учебник для мед.
вузов- дополнительная;
1. А. Петри, К. Сэбин Наглядная медицинская статистика. – М.: ГЭОТАР- Медиа, 2009. – С. 71-86.
2. Зайцев В. М., Лифляндский В. Г., Маринкин В. И. Прикладная медицинская статистика: Учебное пособие. - СПб.: Фолиант, 2006. – С. 262-286.