- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок занимательной математики Математика и жизнь
Содержание
- 2. Пусть каждый запомнит,что можно Любую на
- 3. Цель: развитие познавательного интереса, интеллекта учащихся, расширение
- 4. Математика – это жизнь
- 5. Математика в жизни животных и насекомых.
- 7. Вот, к примеру, пчёлы - удивительное творение
- 9. Тела и фигуры изучает раздел математики,
- 10. Математика и культура.Нам стало интересно, а
- 12. Фасад Парфенона вписывается в прямоугольник, стороны которого
- 14. Математика в живой и неживой природе.Ещё
- 16. Снежинки: ярче примера очаровательной красоты и порядка
- 18. . Где находит свое применение математика?Ответы на этот вопрос приведены в следующей таблице.
- 19. Разминка «На свете лучше нет подруги, Чем математики науки!»
- 20. 1. Разминка (При ответе нужно
- 21. "Посмотри и запомни"
- 23. ВикторинаПодряд стоят 6 стаканов: 3 с водой
- 24. Ответы321 10(5+5):5Цифра2 стакан перелить в пятый1.152.103.5 – 5: 54периметр
- 25. Как называют несколько несложных упражнений, которые обеспечивают
- 26. Разгадай кроссворд
- 28. По горизонтали: 1. Единица измерения углов. 4. Один из компонентов
- 29. По вертикали: 1. Единица измерения площади. 2. Буква греческого алфавита. 3. Математическое
- 30. Ребята, берегите зрение!Физминутка
- 31. Арифметика
- 32. 1. Переложите в каждом равенстве по одной спичке
- 33.
- 34. 6
- 36. Скачать презентацию
- 37. Похожие презентации


































Слайд 3 Цель: развитие познавательного интереса, интеллекта учащихся, расширение знаний
и воспитание стремления к их непрерывному совершенствованию, формирование чувства
солидарности и здорового соперничества.
Слайд 5
Математика в жизни животных и насекомых.
Мир
животных и насекомых - богатый и разнообразный мир живых
существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.Слайд 7 Вот, к примеру, пчёлы - удивительное творение природы.
Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет
(шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?
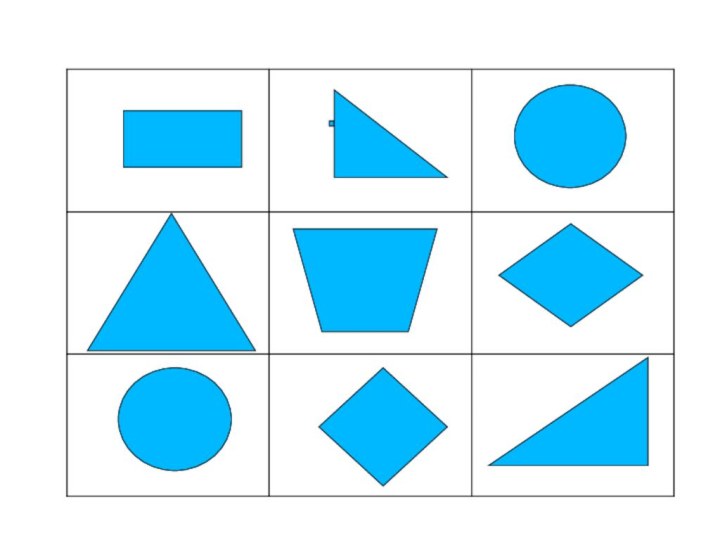
Слайд 9 Тела и фигуры изучает раздел математики, который
называется геометрией. Эта наука возникла в Древней Греции исключительно
из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом, Вы сможете,
Математика геометрических тел и фигур.
Слайд 10
Математика и культура.
Нам стало интересно, а какое
отношение имеет математика к культуре: ведь это и памятники
архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
Слайд 12 Фасад Парфенона вписывается в прямоугольник, стороны которого образуют
так называемое золотое сечение. Длина прямоугольника больше его ширины
примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Слайд 14
Математика в живой и неживой природе.
Ещё Гете
подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно.
Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.Слайд 16 Снежинки: ярче примера очаровательной красоты и порядка в
природе вы не найдете. Изучением снежинок занимался знаменитый Рене
Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».
Слайд 18
. Где находит свое применение математика?
Ответы на
этот вопрос приведены в следующей таблице.
Слайд 20
1. Разминка (При ответе нужно поднять
руку. За правильный ответ - 1 балл.)
Сколько месяцев в
году? 12
2) Назовите шестой месяц года.
(Июнь.)
3) Сколько всего времен года?
(4)
4) Сколько месяцев во времени года?
(3)
5) Какой по счету среди зимних месяцев январь?
(2)
Каков порядковый номер месяца года, заканчивающегося на «Й»?
(5, май.)
6) Предпоследняя буква второго месяца зимы.
(р)
7) Название первого месяца осени.
(Сентябрь.)
8) Кого по осени считают?
(Цыплят.)
9) Назовите четвертую с начала букву русского алфавита.
(г)
10) Какая по счету в алфавите буква «Ю»?
(32-я)
11) Сколько океанов на Земле?
(4)
12) Назовите первую букву названия столицы Франции.
(П)
13) Назовите первую букву названия страны, где столица Токио.
(Я)
14) Сколько дней в високосном феврале?
(29)
15) Какая буква четвертая в слове ПОДЪЕЗД?
(Ъ)
Слайд 23
Викторина
Подряд стоят 6 стаканов: 3 с водой и
3 пустых. Как с помощью одного из этих стаканов
сделать так, чтобы стаканы чередовались пустые и с водой?Слайд 25 Как называют несколько несложных упражнений, которые обеспечивают повышение
физической и умственной работоспособности на весь день, укрепляют организм,
делают его устойчивым к болезням? Физкультминутка
Слайд 28 По горизонтали: 1. Единица измерения углов. 4. Один из компонентов деления. 5. Геометрическая фигура,
которая состоит из трех точек, не лежащих на одной
прямой, и трех отрезков, попарно соединяющих эти точки. 7. Старинная мера длины. 9. Линия без начала и конца, построенная при помощи линейки. 10. Единица измерения массы. 11. Действие, с помощью которого по произведению и одному из множителей находят другой множитель.12. Результат вычитания двух чисел. 13. Основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.Слайд 29 По вертикали: 1. Единица измерения площади. 2. Буква греческого алфавита. 3. Математическое действие с
двумя или несколькими числами. 4. Отрезок, соединяющий две точки окружности и
проходящий через её центр. 6. Раздел математики, изучающий фигуры и их свойства, в переводе на русский язык означает «землемерие». 8. Единица измерения массы.Слайд 32 1. Переложите в каждом равенстве по одной спичке так,
чтобы равенства стали верными:
2. Переложите в каждом равенстве по одной
спичке так, чтобы равенства стали верными:
Слайд 33
№1
Марина мечтала о шоколаде, но ей на покупку не хватало 10 рублей. Вася тоже мечтал о шоколадке, но ему не доставало 1 рубля. Дети решили купить хотя бы одну шоколадку на двоих, но им всё равно не хватило 1 рубля. Какова стоимость шоколадки?
.
Ответ: Стоимость шоколадки – 10 рублей. У Марины нет денег вообще.
№2
Если бы у вас была только одна спичка, и вы вошли в комнату, где есть керосиновая лампа, камин и газовая плита, чтобы вы зажгли первым делом?
Ответ: Спичку
Если бы завтрашний день был вчерашним, то до воскресенья осталось бы столько дней, сколько прошло от воскресенья до вчерашнего дня. Какой же сегодня день?
Ответ: среда
№3
Слайд 34 6
№1
У старшего брата две конфеты, а у младшего 12 конфет. Сколько конфет должен отнять старший у младшего, чтобы справедливость восторжествовала, и между братьями наступило равенство?
Ответ: 5
№2
Если бы завтрашний день был вчерашним, то до воскресенья осталось бы столько дней, сколько прошло от воскресенья до вчерашнего дня. Какой же сегодня день?
Ответ: среда
№3
Когда отцу было 37 лет, то сыну было 3 года, а сейчас сыну в 3 раза меньше лет, чем отцу. Сколько лет сейчас отцу и сколько лет сыну?
Ответ:51, 17