Презентация на тему Устойчивость стержней. Продольно - поперечный изгиб

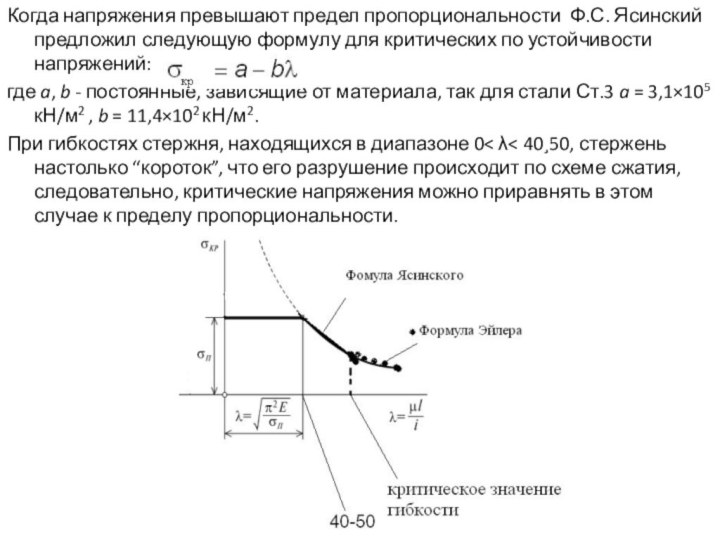
20.1 Общие понятия о продольном изгибе
Наряду с выполнением условий

прочности и жесткости, необходимо обеспечить и устойчивость конструкций.

Под устойчивостью понимается свойство способности системы сохранять свое первоначальное равновесное состояние.

Явление перехода системы от одного равновес­ного состояния к другому равновесному состоянию, называется потерей устойчивости системы.

Значения внешних сил, при которых происходит потеря устойчивости, называются критическими.

      Основная задача теории устойчивости заключается в определении критического значения внешних сил и ограничение их величин таким образом, чтобы исключить возможность потери устойчивости заданной системы в эксплуатационных режимах.

стержня определялось как простое сжатие, то при P > Pкр сжатие сопровождается

изгибом. Это означает, что при P = Pкр  происходит потеря устойчивости системы.






Для гибких стержней потеря устойчивости может наступить при напряжениях, значительно меньших предела прочности материалов.

нагрузка, при которой стержень данной длины и площади поперечного

сечения теряет устойчивость, не зависит от предела прочности материала, а зависит только от формы поперечного сечения, модуля упругости (жесткости) материала и условий закрепления концов стержня при нагружении.

При дальнейшем увеличении нагрузки изогнутый стержень разрушается. Такой вид потери несущей способности называется общей потерей устойчивости.

При отсутствии общей потери устойчивости нагруженная сжатием конструкция может выйти из строя из-за местных деформаций отдельных участков. Такой вид потери несущей способности называется местной потерей устойчивости.

При местной потере устойчивости происходит выпучивание, излом или появление гофра на каком-либо элементе сложного профиля

с простейшей задачи



 Эйлер получил зависимость для критической силы которая

носит название «Формула Эйлера» (без вывода) :









где µ - коэффициент приведения длины (зависит от способов закрепления концов стержня). Он показывает, во сколь­ко раз следует изменить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась бы критической силе стержня длиной l в рассматриваемых условиях закрепления.

решение Эйлера подтверждалось не во всех случаях. Причина состоит

в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень работает в пределах упругих деформаций по закону Гука. Следовательно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности.
Найдем границы применимости решения Эйлера:

где   - радиус инерции сечения.
Введем понятие гибкости стержня:

Тогда уравнение Эйлера принимает вид:

Приравнивая критическое напряжение к пределу пропорциональности, получим предельное значение гибкости:

формулу для критических по устойчивости напряжений:
где a, b - постоянные,

зависящие от материала, так для стали Ст.3 a = 3,1×105 кН/м2 , b = 11,4×102 кН/м2.
При гибкостях стержня, находящихся в диапазоне 0< λ< 40¸50, стержень настолько “короток”, что его разрушение происходит по схеме сжатия, следовательно, критические напряжения можно приравнять в этом случае к пределу пропорциональности.

на устойчивость
Как правило, основная проблема при расчете сжатых

стержней состоит в том, чтобы сжимающие напряжения σ не превышали бы критических значений по устойчивости σкр , т.е.


При продольном изгибе центрально сжатый стержень теряет несущую способность, когда напряжения в его поперечных сечениях достигают критических значений. Поэтому необходимо ввести в расчет коэффициент запаса устойчивости n по отношению к критическим напряжениям, с помощью которого и определяется допускаемое напряжение при расчете на устойчивость:




Расчеты на продольный изгиб разделяют на два типа: определение допускаемых нагрузок и подбор сечения.