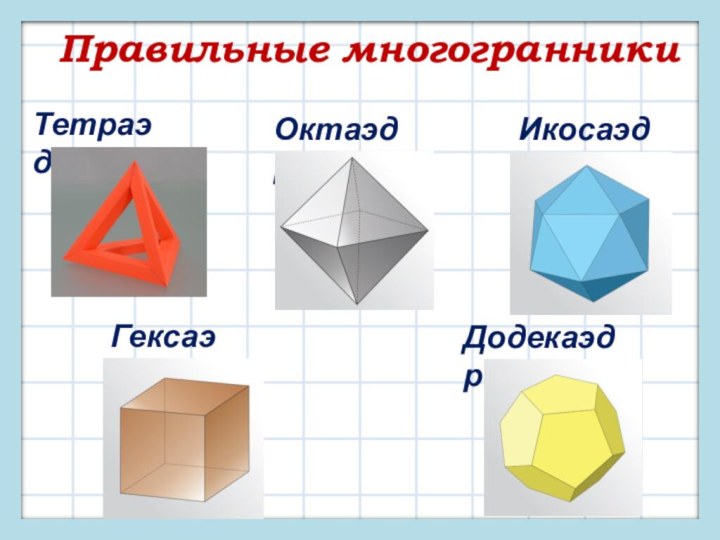
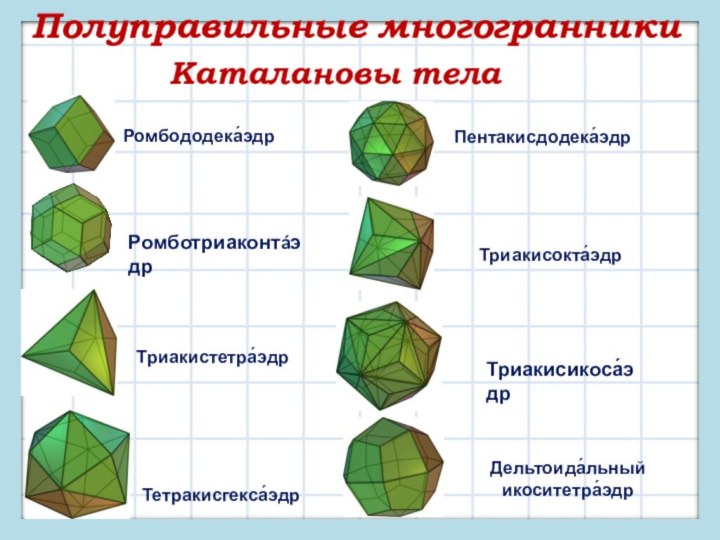
кроме тех, которые изучают в школе
выяснить ,существуют ли геометрические
фигуры кроме тех, которые изучают в школе.Задачи:
Выяснить, какие фигуры знают одноклассники;
Узнать что такое геометрическая фигура;
Узнать, какими бывают геометрические фигуры.
Анкетирование одноклассников, обработка результатов;
Определение «геометрической фигуры» в разных источниках;
Сделать классификацию геометрических фигур;
Найти фигуры, соответствующие классификации;
Найти сведения о новых фигурах.
Работа с учебной и научно-популярной литературой, ресурсами сети Интернет;
Анкетирование, анализ результатов.
Построение некоторых фигур.
названия новых фигур и некоторые их свойства