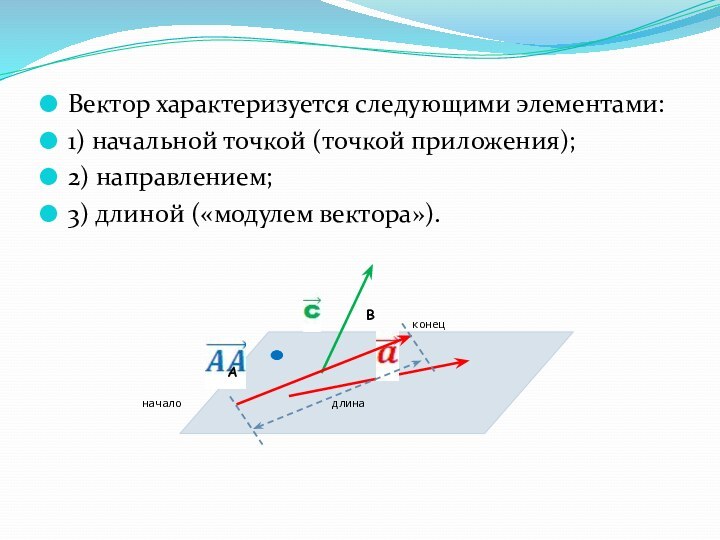
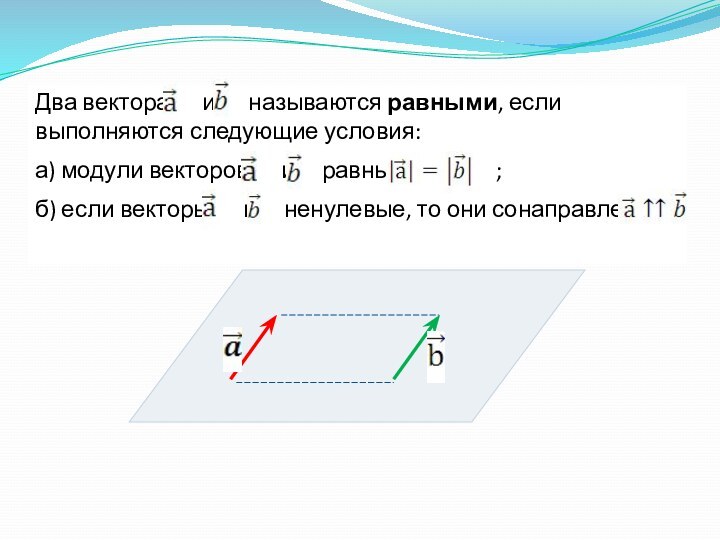
направленный отрезок, т.е. отрезок, для которого указано, какая из
концевых его точек считается началом, какая – концом отрезка.А
В
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

![Элементы линейной алгебры Вектором [От латинского vector – везущий, несущий] называется направленный отрезок, т.е. отрезок,](/img/tmb/13/1242455/3a3e018cae447157f0db785252386a60-720x.jpg)



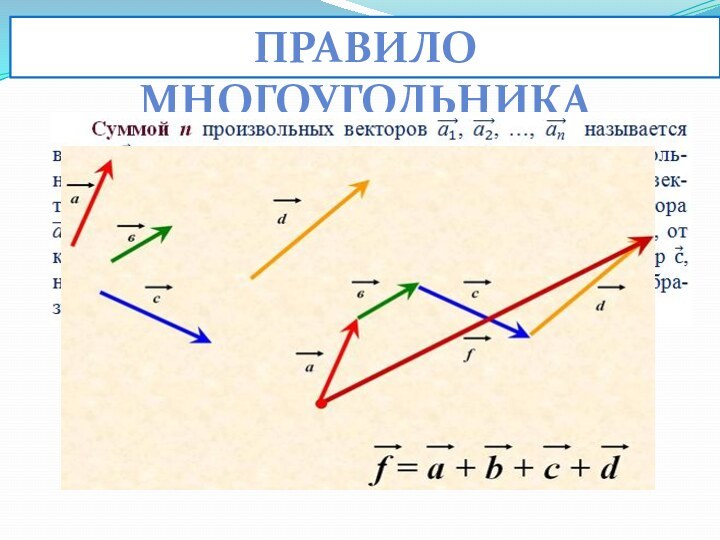
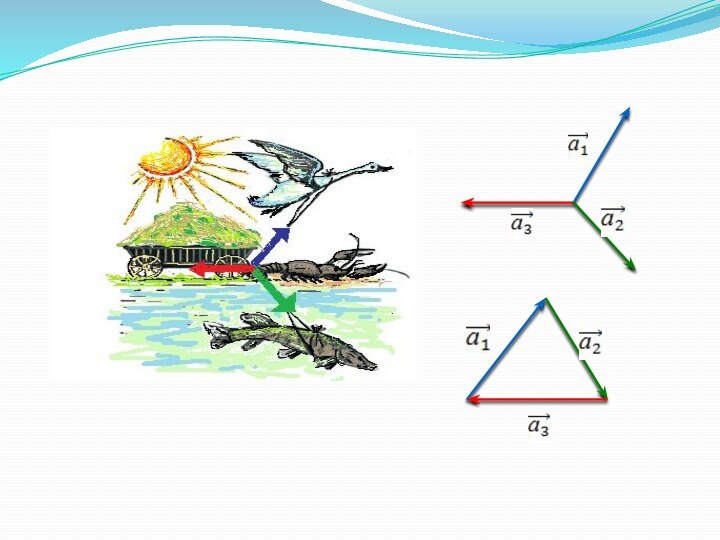



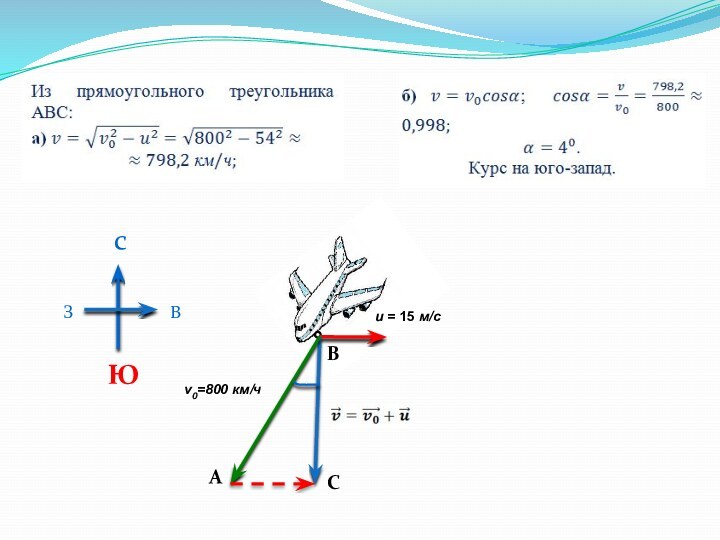





А
В
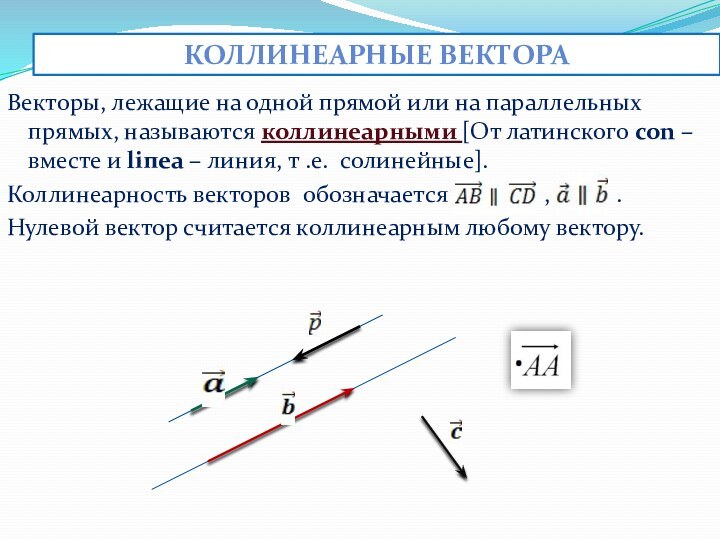
Коллинеарные вектора
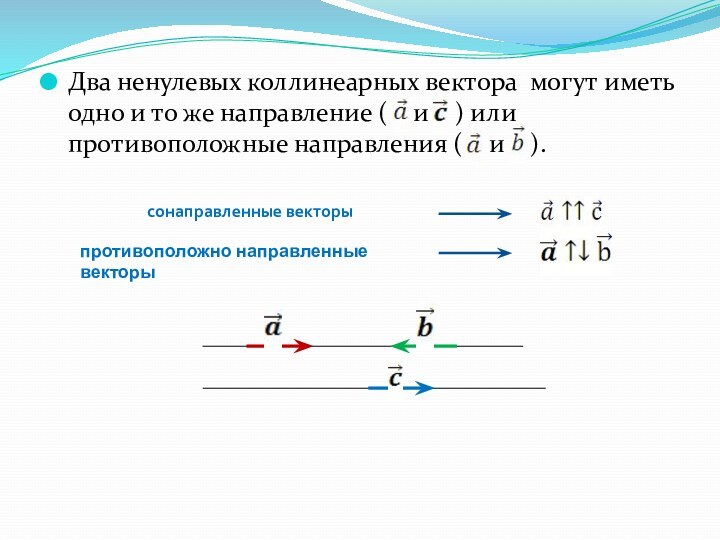
сонаправленные векторы
противоположно направленные векторы
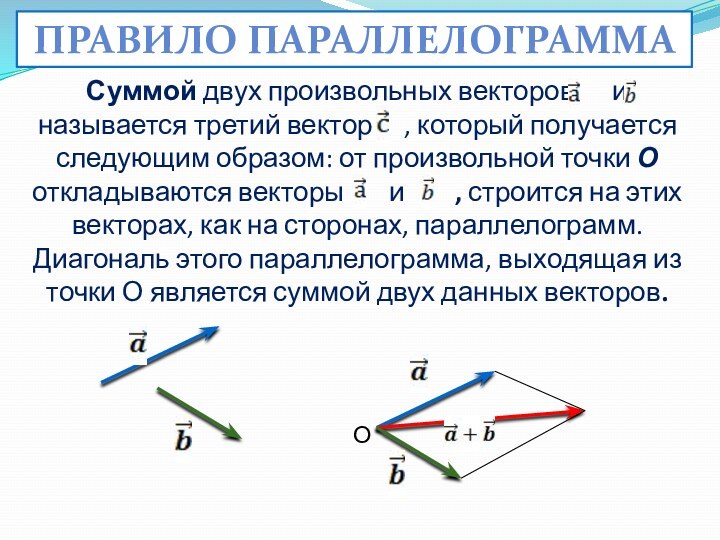
Правило параллелограмма
О
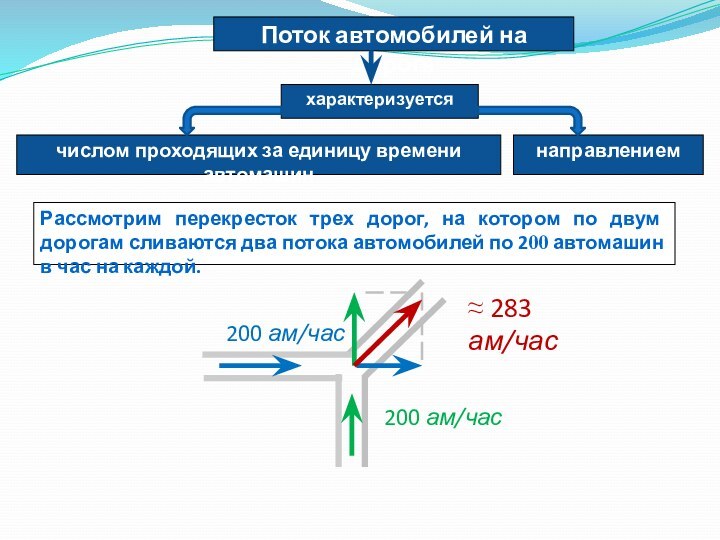
200 ам/час
200 ам/час
283 ам/час
Поток автомобилей на дороге
характеризуется
числом проходящих за единицу времени автомашин
направлением
Произведение нулевого вектора на произвольное число или числа нуль на произвольный вектор есть нуль–вектор.
Произведение вектора на число обладает следующими свойствами:
1)
2)
3)
4)
Пусть вектор коллинеарен ненулевому вектору .
Возможны следующие три случая:
l) ; 2) ; 3) .