Слайд 2
Сопротивление движению
Сопротивления могут быть обусловлены вязкостными или инерционными
силами.
Вязкостные силы зависят от внутреннего трения между частицами
жидкости;
Инерционные – от способности частиц жидкости оказывать сопротивление изменению своего движения.
Слайд 3
В общем случае имеют место оба вида потерь
– по длине и местные, значение которых суммируют
hΣ
= Σ hl + Σ hM ,
где Σ hl – сумма потерь по длине разных участков трубы, Σ hM – сумма всех местных потерь.
Сила внутреннего трения
T = - μ ω dv/dn
Касательное напряжение τ = - μ dv/dn
Слайд 4
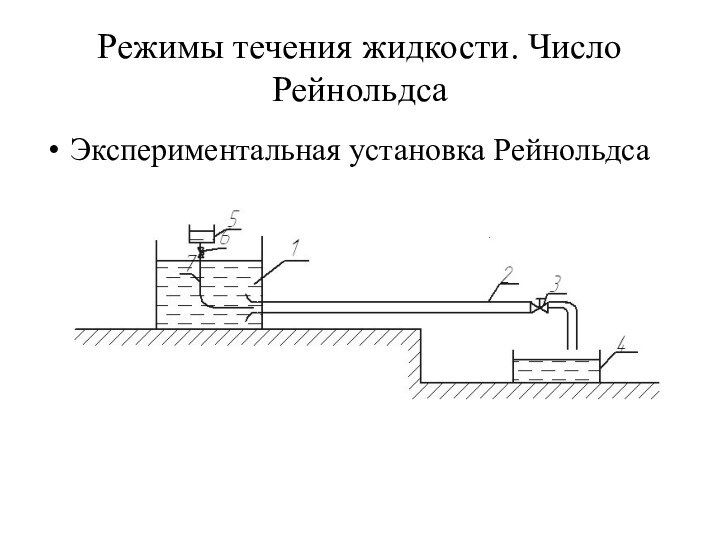
Режимы течения жидкости. Число Рейнольдса
Экспериментальная установка Рейнольдса
Слайд 5
Число Рейнольдса
Re
= Vdρ / μ = Vd / ν
Reкр=2320 –критическое
число
При Re < Reкр- режим течения ламинарный;
При Re > Reкр - режим течения турбулентный.
Переходный режим считается при
Re = 2320–4000.
Слайд 6
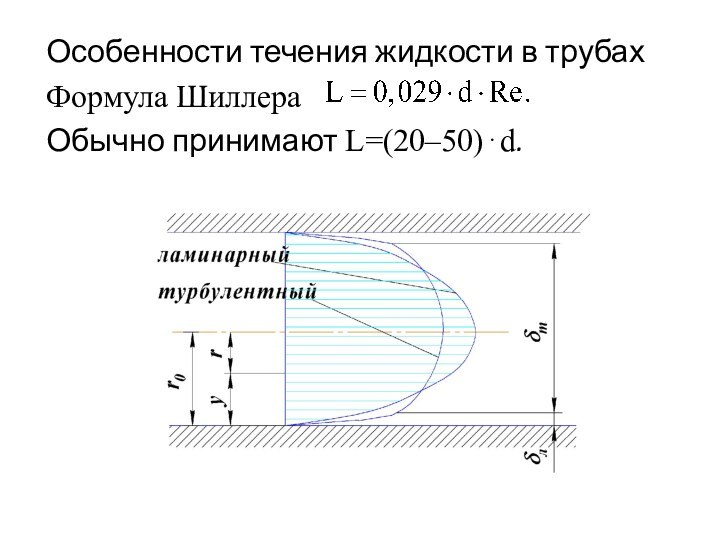
Особенности течения жидкости в трубах
Формула Шиллера
Обычно принимают L=(20–50)d.
Слайд 7
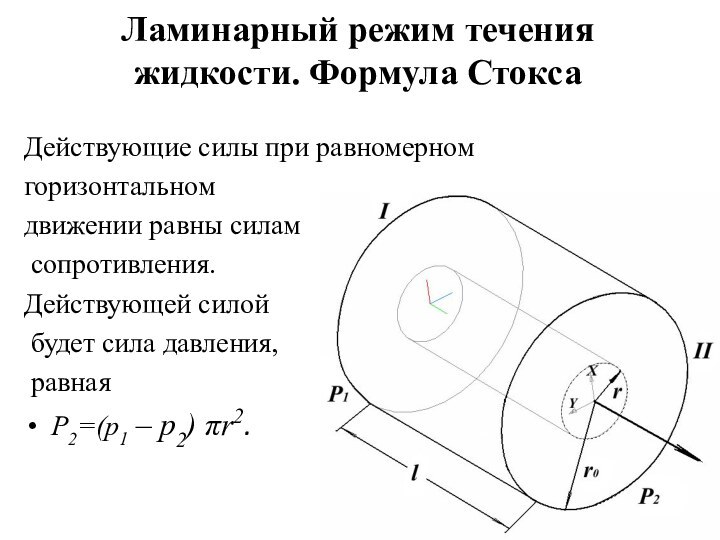
Ламинарный режим течения жидкости. Формула Стокса
Действующие силы при
равномерном
горизонтальном
движении равны силам
сопротивления.
Действующей силой
будет сила давления,
равная
P2=(р1 – р2) πr2.
Слайд 8
Сила трения определяется произведением площади поверхности цилиндра 2πr·l
и касательного напряжения
Сумма всех сил при равновесии должна
быть равна нулю.
Разделяя переменные, получим:
интегрируя, находим
Закон Стокса
При r = 0
Тогда предыдущее выражение можно переписать так
(p1 – p2) π r 2 = 2 π r l τ
τ = pтр r / 2 l
Слайд 10
Закон Гагена – Пуазейля
ds =2πr∙dr
dq=v∙ds ?
Подставляя значение
скорости
Найдем
Или
Это
формула для расхода жидкости при ламинарном режиме течения жидкости.
Слайд 11
Расход жидкости по тубе, выраженный через среднюю скорость
Q=πr02vср
Приравнивая к расходу по формуле Пуазейля
Выразим vср
Сравним это выражение с формулой определяющей максимальную скорость по оси трубы
Следовательно
Слайд 12
Потери напора при ламинарном движении
или так как
Заменив
μ = νρ, d = 2r0, получим
Выражение (6.7) называется законом Гагена-Пуазейля и позволяет определить потери энергии при ламинарном течении вязкой жидкости в круглой трубе при заданном расходе Q на участке длиной l.
Слайд 13
Если в формулу Гагена –Пуазейля
вместо Q подставить
его
выражение через скорость и площадь трубы,
то получим
Последнее
выражение можно представить так
Учтя гидр.коэф. трения , (коэффициент Дарси) получим формулу
Дарси-Вейсбаха
Слайд 14
Распределение касательных напряжений
Если напряжения на стенке при r=r0
принять
равным τ = τ0 , то
И выражение для
касательных
напряжений τ будет иметь вид
Слайд 15
Частные случаи ламинарного движения
откуда dτ= 0 или τ=const=C1
Согласно
закона Ньютона
Интегрируя,
Очевидно, что v=0 при y=0 и v=u при y=b. Отсюда
подставляя, получим:
Слайд 16
Фрикционное течение в кольцевом зазоре
При малом относительном зазоре
(b/D
сохраняет ламинарный характер для чисел Рейнольдса , если
вращается вал, а подшипник неподвижен.
В противном случае ламинарный режим будет в
области чисел Рейнольдса Re≤2000 , а само число определяется по выражению
Слайд 17
Плоское криволинейное течение жидкости
или
Интегрируя
Граничные условия v=u при r=R1
V = 0 при r = R, находим распределение v, τ
Слайд 18
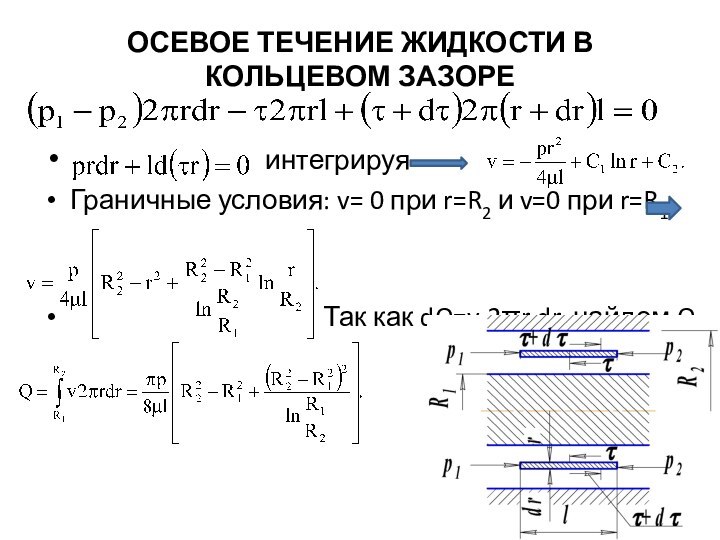
ОСЕВОЕ ТЕЧЕНИЕ ЖИДКОСТИ В КОЛЬЦЕВОМ ЗАЗОРЕ
интегрируя
Граничные условия: v= 0 при r=R2 и v=0 при r=R1
Так как dQ=v·2r·dr, найдем Q
Слайд 19
Течение между неподвижными пластинами шириной B
Принимая и
вычисляя интеграл этого уравнения с учетом граничных условий –
равенство нулю скорости на стенках – имеем
Слайд 20
Зазор между параллельными пластинами, одна из которых подвижна
При
реверсе пластины (-u), знак перед двумя первыми членами
формулы меняется
на
противополож-
ный