Презентация на тему Модель Изинга. Приложение к физике магнитных явлений

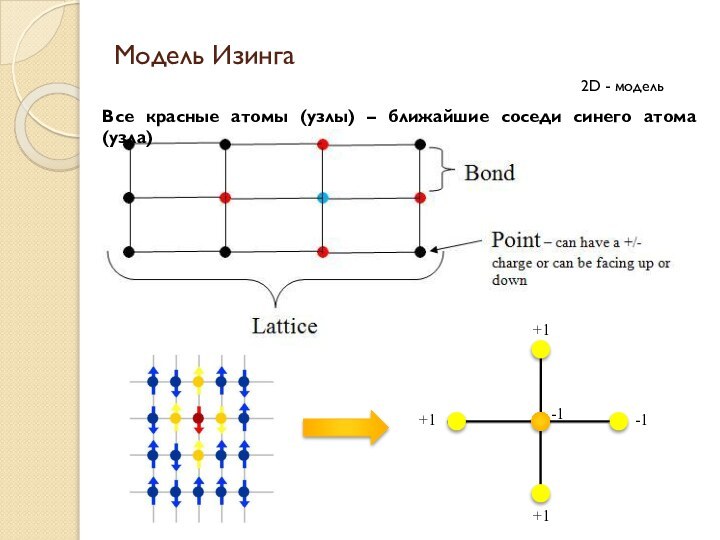
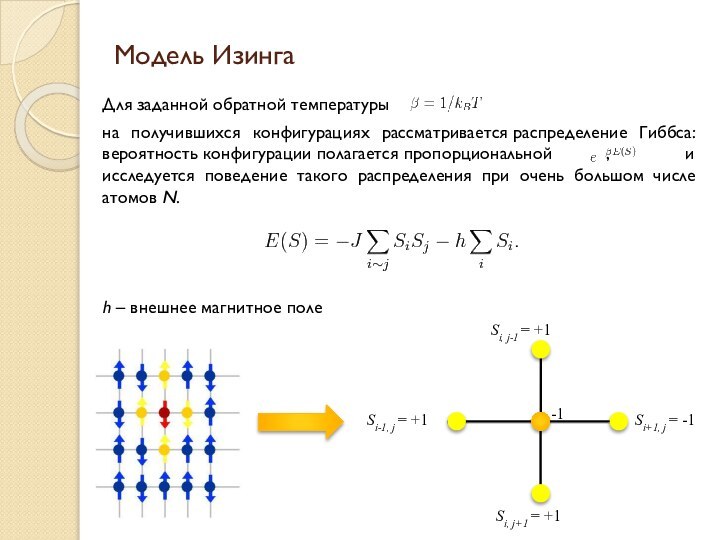
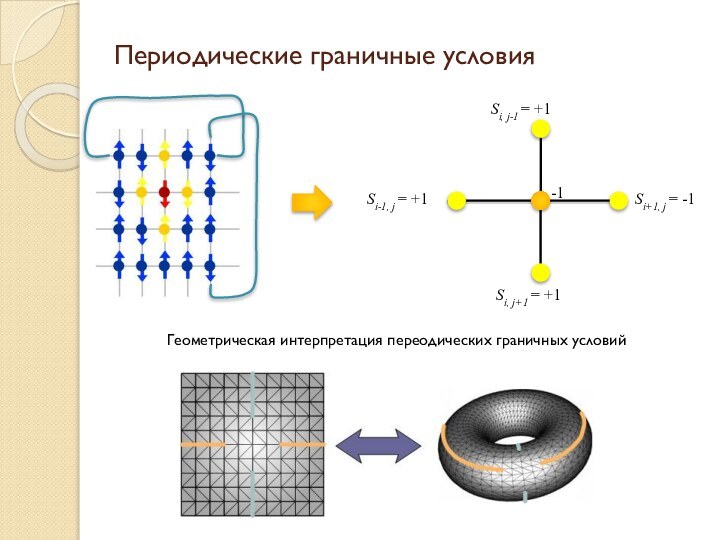
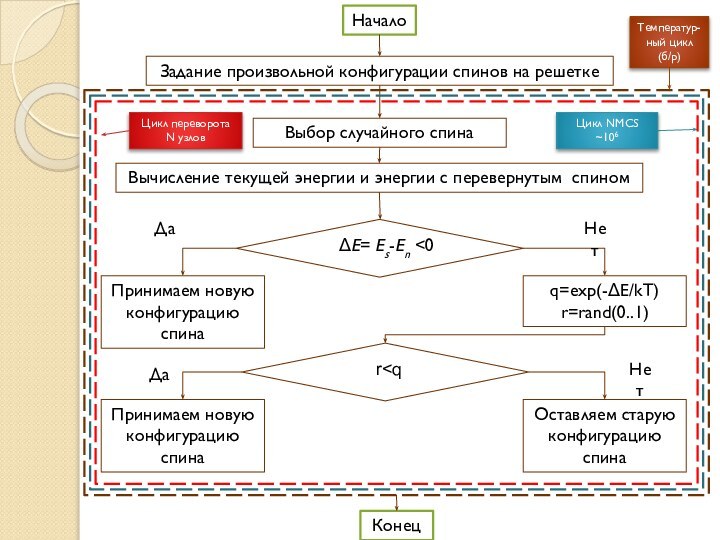
кристаллической решётки (рассматриваются не только трёхмерные, но и одно-

и двумерные случаи) сопоставляется число, называемое спином и равное +1 или −1 («поле вверх»/«поле вниз»). Каждому из  возможных вариантов расположения спинов (где N — число атомов решётки) приписывается энергия, получающаяся из попарного взаимодействия спинов соседних атомов:


J>0 – ферромагнитный обмен
J<0 – антиферромагнитный обмен
J=0 – обмен отсутствует

Модель Изинга

синего атома (узла)

2D - модель
+1
+1
+1
-1
-1

конфигурации полагается пропорциональной  , и исследуется поведение такого распределения при

очень большом числе атомов N.



h – внешнее магнитное поле

Модель Изинга

Si, j-1 = +1

Si-1, j = +1

Si, j+1 = +1

Si+1, j = -1

-1

= +1
Si+1, j = -1
-1
Периодические граничные условия
Геометрическая интерпретация переодических

граничных условий

текущей энергии и энергии с перевернутым спином
Принимаем новую конфигурацию

спина

ΔE= Es-En <0

Да

q=exp(-ΔE/kT)
r=rand(0..1)

Нет

r

Принимаем новую конфигурацию спина

Да

Оставляем старую конфигурацию спина

Нет

Температур-ный цикл (б/р)

Цикл NMCS
~106

Конец

Цикл переворота N узлов

величин С, M, E, 
C = C/(NMCS - wasteNMCS)/nstep
В

этом цикле происходят только перевороты спинов

Накопление значений величин С, M, E, 
C = С + [-2]/T

Первые 500-1000 шагов NMCS отбрасываются (wasteNMCS)

Замер ч/з 100 шагов (nstep)

Алгоритм Метрополиса

1 раз
ΔE = 8J
ΔE = 4J
ΔE = 0
ΔE

= -4J

ΔE = -8J

Значения сохраняются в локальных переменных и используются в программе

Адиабатическое изменение температуры (МКЭ)
- Решеточная теплоемкость
Nc полное число шагов

Монте-Карло, N0 число шагов Монте-Карло для установления равновесия физических величин, индекс i определяет шаг Монте-Карло

четкий переход