Слайд 2
План
Определение числового неравенства
Свойства числового неравенства
Определение неравенства с одной
переменной
Область определения неравенства с одной переменной
Решение неравенства
Равносильные неравенства
Иррациональные неравенства
Часто
используемые неравенства
Неравенства с модулем
Методы доказательств неравенств
Слайд 3
Числовое неравенство
Числовым неравенством называется запись вида
a > b ( a < b ),
где a, b − числа.
При этом a > b считается истинным тогда и только тогда, когда разность
a – b есть положительное число
( a < b если разность a – b есть отрицательное число).
Слайд 4
Допускаются знаки ≥ и ≤ .
( a ≥
b ) ( a > b ) или
( a = b )
( a ≤ b ) ( a < b ) или ( a = b )
Запись a > 0 говорит о том, что число а положительное.
Запись a ≥ 0 говорит о том, что число а неотрицательное.
Слайд 5
Свойства
Если a > b и b > c,
то a > c.
Если a > b, то для
любого числа с
a + c > b + c .
Если a + b > c, то a > c – b.
4. Если a > b и c > d => a + c > b + d
Следствие. Если a > b, c > d =>
a – d > b – c.
Слайд 6
Если a > b, c > 0 =>
ac > bc,
Если a > b, c < 0
=> ac < bc.
6. Если a > b > 0 и c > d > 0 => ac > bd.
7. Если a ≥ b > 0 и c > d > 0 =>
Слайд 7
Следствие. Если a = b = 1, то
при
c > d > 0 получим
.
Запишем это важное
следствие таким образом.
Если a > b > 0 =>
Слайд 8
8. Если a > b ≥ 0 =>
an > bn, n N.
Следствие. Если n =
2, то из
a > b ≥ 0 => a2 > b2.
9. Если a > b => a2n+1 > b2n+1, n N.
Следствие. Если n = 1, то из
a > b => a3 > b3.
Слайд 9
10. Если a > b ≥ 0 =>
11. a > b =>
Следствие. Неравенство a2 > b2 имеет место в том и только в том случае, если |a| > |b|.
Слайд 10
Неравенство с одной
переменной
Пусть даны две функции f(x) и
g(x), где х – переменная, с областями определения D1(f)
и D2(g) соответственно. Запись вида
f(x) > g(x) ( f(x) < g(x))
называется неравенством с одной переменной, если поставлена задача:
найти все те значения x, при которых выражение f(x) > g(x) истинно.
Слайд 11
f(x) > g(x) ( f(x) < g(x))
Вместо знака «больше» («меньше») может быть использован знак ≥
(больше либо равно) или знак ≤ (меньше либо равно), или знак ≠.
Слайд 12
Область определения неравенства
Областью определения неравенства (ОДЗ)
f(x) > g(x)
называется
пересечение областей опре-
деления функций, входящих в левую и правую
части неравенства.
Например, ,
ОДЗ: х2 – 1 ≥ 0;
х + 2 ≠ 0.
Слайд 13
Пример на нахождение
области определения
х2 <
В этом
примере D(х2) = R; а область определения
правой части = [1; + ∞).
Их пересечение есть промежуток [1; + ∞).
Обозначим область определения неравенства ОДЗ (область допустимых значений).
Слайд 14
Решение неравенства
Пусть х0 – какое–либо число из области
определения неравенства. Неравенство
f(x) > g(x) называется истинным при
х =
х0, если при подстановке числа х0 вместо х данное неравенство обращается в верное числовое неравенство. В этом случае говорят, что число х0 является решением неравенства.
Слайд 15
Пусть множество М – какое-нибудь подмножество ОДЗ (М
может совпадать с ОДЗ или быть пустым). Неравенство f(x)
> g(x) называется истинным на множестве М, если оно истинно для любого числа х из множества М. В этом случае говорят, что множество М является решением неравенства.
Слайд 16
Что значит
«решить неравенство»
Решить неравенство f(x) >
g(x)
это значит, найти все его решения, или же
доказать, что решений нет.
В последнем случае говорят, что неравенство имеет пустое множество решений.
Слайд 17
Чаще всего решения неравенства – это один промежуток
или объединение нескольких числовых множеств.
Но может оказаться, что решением
неравенства является одно число, а не промежуток, или несколько чисел.
Также решением неравенства может быть пустое множество.
Слайд 18
Примеры
Преобразования неравенства с одной
переменной происходят по тем же
правилам, что и для числового неравенства.
1)
х2 ≤ 0.
Решение. х2 < 0 или х2 = 0.
Ответ: х {0}.
2) х2 > 0.
Ответ: х (– ∞;0) U (0; + ∞).
0.
Ответ: х Ø.
4)
Ответ: х
(– ∞; –1] U [1; + ∞).
5)
Ответ: х (– ∞;0) U (0; + ∞).
6)
Ответ: х [1; + ∞).
Слайд 20
Равносильные неравенства
Два неравенства называются равносильными, если каждое решение
первого неравенства является решением второго, и обратно, каждое решение
второго неравенства является решением первого, или же оба неравенства не имеют решений (пустое множество решений).
Слайд 21
Пример
Равносильны или нет следующие два неравенства:
х2
– 1 ≥ 0
и
Решение первого: Решение второго:
(– ∞; –1] U [1; + ∞). R
Ответ: не равносильны
Слайд 22
Методы решения
Методы решения зависят от вида неравенства и
изучаются по мере изучения соответствующих функций. Можно отметить такие
неравенства: рациональные, иррациональные, тригонометрические, показательные, логарифмические, неравенства с параметром, комбинированные и др.
Слайд 23
С чего начать решение?
Начинать решение следует с ОДЗ.
ОДЗ
выписывается точно так же, как для уравнений. В ОДЗ
может быть система рациональных неравенств. Рациональные неравенства решаются методом интервалов.
Если есть система неравенств, то вспомним, как решается система неравенств.
Слайд 24
Система неравенств
Чтобы решить систему неравенств, надо решить каждое
рациональное неравенство отдельно и пересечь найденные решения.
При решении иррациональных
неравенств также будут получаться системы рациональных неравенств. Найдя множества их решений, надо не забыть пересечь их с ОДЗ.
Слайд 25
Иррациональные неравенства
Простейшее иррациональное неравенство имеет вид
Если знак
в другую сторону, то метод решения будет другой.
Его рассмотрим
далее через четыре слайда.
Слайд 26
ОДЗ: f(x) 0.
Решение.
По определению арифметического квадратного
корня из выражения, содержащего х, левая часть неравенства неотрицательна,
т.е.
По свойству 1 неравенств (транзитив-ность) правая часть неравенства также будет неотрицательна.
Слайд 27
И можно будет возвести обе части неравенства в
квадрат. Тогда напишем систему.
На ОДЗ неравенство равносильно системе
g(x) 0;
f(x) g2(x).
Получили систему рациональных нера-венств. Решаем и пересекаем с ОДЗ. Выписываем слово «Ответ» и сам ответ.
Слайд 28
Для пересечения удобно нарисовать числовые оси друг под
другом,
совместив начала отсчета. Решение каждого неравенства надо изобразить
на своей оси. На одной из осей следует нарисовать ОДЗ всей системы. После пересечения выписывайте ответ.
Слайд 29
Пример
Решим неравенство
ОДЗ: х2 – 3х – 10
0;
Корни х1 = –2; х2 = 5.
Имеем
систему 8 – х > 0;
х2 – 3х – 10 < (8 – x)2.
x < 8;
13x < 74
Ответ:
х (; 2] [ 5; +);
Слайд 30
Иррациональные неравенства
Иррациональное неравенство с другим знаком имеет вид
Метод
решения надо записать в блокнот и запомнить.
Начинаем с ОДЗ:
f(x) 0.
Слайд 31
Правая часть может быть отрицательной и неотрицательной. Поэтому
надо рассмотреть два случая:
1 случай: правая часть отрицательна.
2 случай:
правая часть неотрицательна.
1 случай
Тогда имеем систему: g(x) < 0;
Слайд 32
g(x) < 0;
В левой
части 2-го неравенства стоит неотрицательное число, а в правой
– отрицательное. Такое неравенство всегда верно, и его решать не надо. Остается решить только первое неравенство g(x) < 0 и пересечь его с ОДЗ.
Итак, первый случай рассмотрели.
Слайд 33
2 случай
Правая часть 0, т.е. имеем систему
g(x) 0;
Обе части второго неравенства
неотрицательны, сл-но, по свойству неравенств можем возвести в квадрат.
Слайд 34
На ОДЗ имеем равносильную систему:
g(x) 0;
.
Заметим, что из второго неравенства вытекает, что ОДЗ автоматически выполняется.
Решаем эту систему.
В ответ выписываем объединение решений первого и второго случаев.
Слайд 35
Пример
Решим неравенство
ОДЗ: х + 2 0,
т.е. х [2; +).
1 сл.
2 сл.
2х + 3 < 0; 2x + 3 0;
; всегда верно x + 2 (2x + 3)2.
x < – 1,5; x – 1,5;
x [2; – 1,5) . 4x2 + 11x + 7 0.
Корни –7/4; –1.
x [1,5; –1]
Ответ: x [2; –1].
Слайд 37
Схема решения
ОДЗ: {f(x) 0}
Def(f) Def(g);
1 сл.
2 сл.
g(x)< 0; g(x) 0;
g(x) < 0; g(x) 0,
; всегда верно f(x) g(x)2.
{g(x) < 0} ОДЗ; ОДЗ;
х M1 х M2.
Ответ: х M1 M2.
Решение системы
Слайд 38
Некоторые неравенства
Для любых действительных чисел а и b
выполняется неравенство
а2 + b2 2аb
Доказательство
Перенесем 2аb в
левую часть и получим
а2 + b2 2аb 0, или ( а – b)2 0.
а2 + b2
2|аb|
Это неравенство вытекает из
( |а| – |b|)2 0.
Слайд 40
Если a и b – действительные числа одного
знака (т. е. ab > 0), то
Доказательство
Умножим обе части неравенства
а2 + b2 2аb на положительное число >0.
Получим .
Равенство при a = b
Слайд 41
Следствие
Если a – положительное число (т. е. a>0),
то
Равенство при a = 1
Слайд 42
Неравенство о среднем арифмети-
ческом и среднем
геометрическом
Если a 0 и b 0, то
т. .е. среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического.
Доказательство
a + b 2ab,
Слайд 43
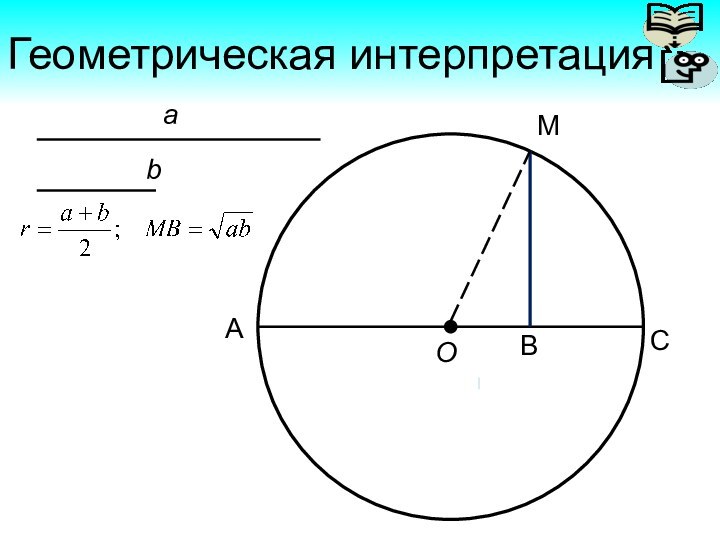
Геометрическая интерпретация
a
b
A
B
C
O
Слайд 44
Неравенства с модулями
Неравенство
|a| < b
имеет место тогда и только тогда, когда выполняется следующее двойное неравенство
b < a < b.
Слайд 45
Следствие
Очевидно, что
a |a|.
Из a |a| следует, что
– |a| a |a|
Слайд 46
Неравенство «треугольника»
Для любых действительных чисел a и b
выполняется неравенство
|a + b| |a| + |b|.
Доказательство
Из следствия
на предыдущем слайде
– |a| a |a|
– |b| b |b|
Сложим неравенства:
– (|a| + |b|) a + b |a| + |b|
Слайд 47
|a + b| |a| + |b|
Сложим неравенства:
– (|a| + |b|) a + b |a|
+ |b|
Вспоминая, что двойное неравенство
D C D равносильно |С| D, получим следующее неравенство
|a + b| |a| + |b|.
Читается
«Модуль суммы двух чисел не превос-ходит суммы модулей этих чисел»
Слайд 48
Для любых действительных чисел a и b выполняется
неравенство
|a b| ||a| |b||.
Без доказательства
Слайд 49
Методы доказательства неравенств
Используя определение
Цепочкой слева направо
Цепочкой справа налево
Используя
уже доказанное
Столбиком
Используя оценку каждого неравенства
Слайд 50
Пример 1
Докажите, что для любых действительных чисел а
и b имеет место неравенство
а4 + b4 ≥ a3b
+ ab3.
Доказательство (используя определение)
а4 + b4 – a3b − ab3 = a3( a – b) – b3(a – b)=
= (a – b)(a3 – b3) = (a – b)(a – b)(a2 + ab +b2)
= (a – b)2(a2 + ab +b2) ≥ 0.
Слайд 51
Пример 2
Докажите, что для любых действительных чисел а,
b и с имеет место неравенство
а2 + b2 +
с2 ≥ ab + bс + ac.
Доказательство (используя уже доказан-ные неравенства)
Имеем a2 + b2 ≥ 2ab;
b2 + c2 ≥ 2bc;
c2 + а2 ≥ 2ac.
Сложим и разделим на 2. Неравенство доказано.
Слайд 52
Задачи для самостоятельной
работы
1. Докажите, что если действительные числа
а, b и с таковы, что
a + b
+ c = 0, то имеет место неравенство
ab + bc + ca ≤ 0.
2. Докажите, что если a2 + b2 = 1, то
|a + b| ≤ √2.
3. 5a2 – 6ab + 5b2 ≥ 0.
4. a2 + b2 + 1 ≥ ab + a + b.
Слайд 53
Домашнее задание
Выучите основные свойства неравенств и научитесь их
доказывать.
Запомните метод решения простых иррациональных неравенств двух видов.
Выучите наиболее
часто встречающиеся неравенства (для сомневающихся в необходимости:
они помогут сдать ЕГЭ)