x
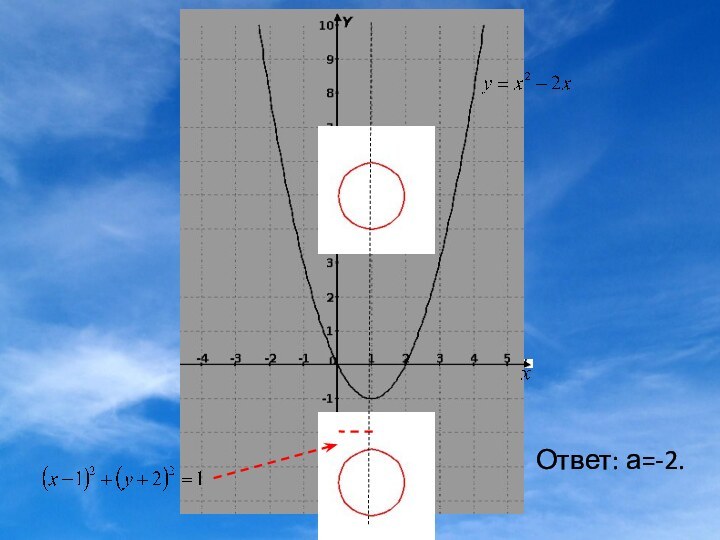
ее является парабола с вершиной (2;4), ветви которой направлены вниз.
б) если х ≥4, то|x-4|=х-4, функция имеет вид у=х2-4х. Графиком ее является парабола с вершиной (2;-4), ветви которой направлены вверх.
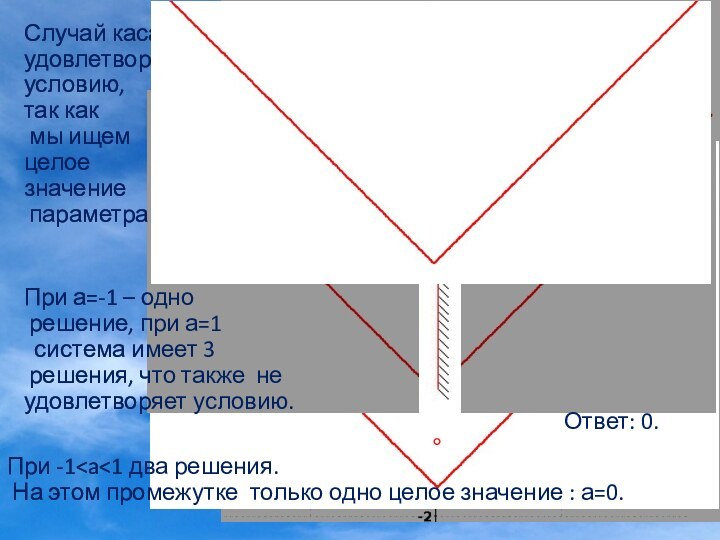
в) графиком функции у=а является прямая, параллельная оси Ох, проходящая через точку (0;а).
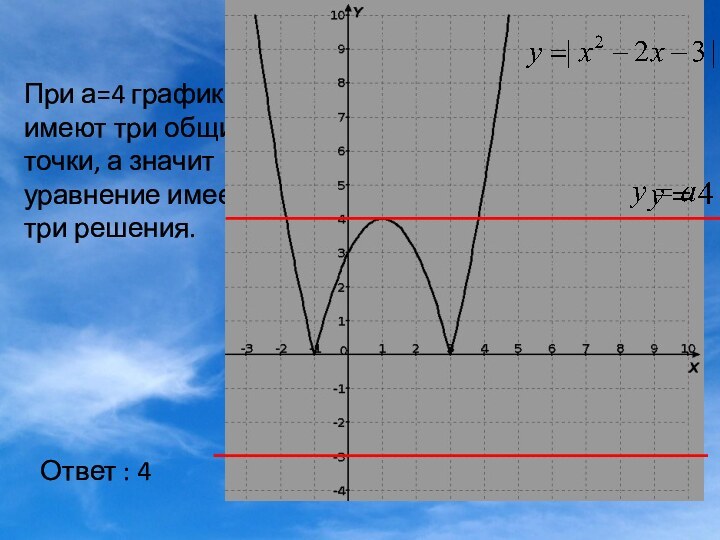
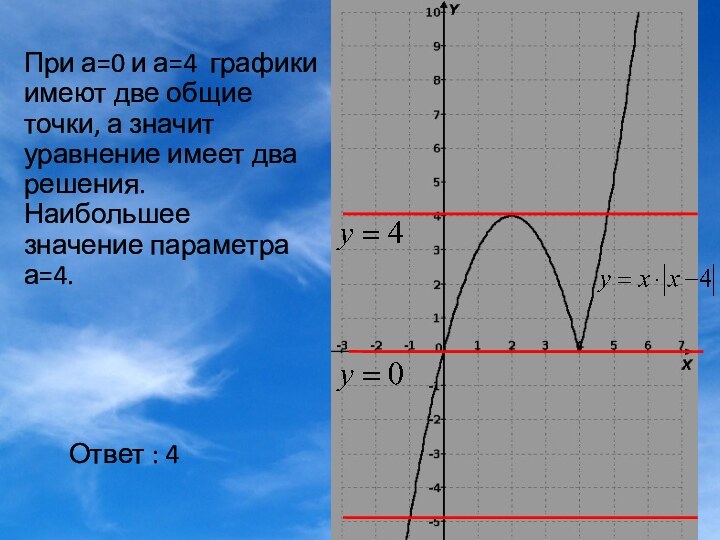
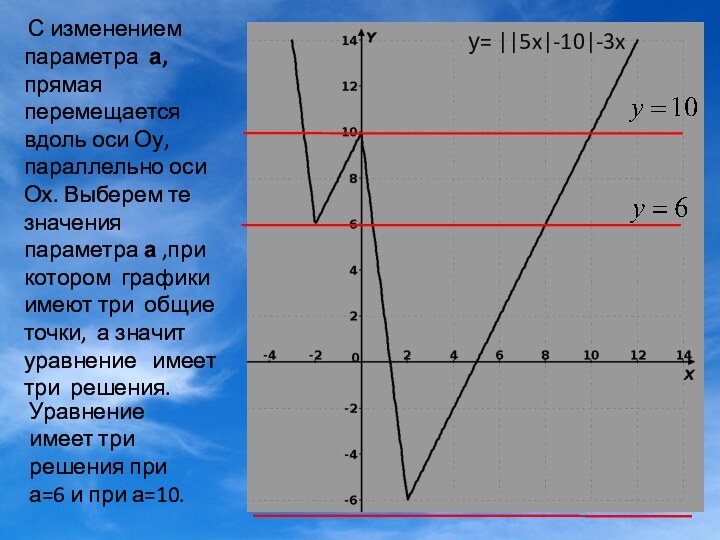
С изменением параметра а, прямая перемещается вдоль оси Оу, параллельно оси Ох. Уравнение имеет столько решений, сколько общих точек имеют графики. Графики могут иметь одну , две или три общие точки. Выберем те значения параметра а ,при котором графики имеют две общие точки, а значит уравнение имеет два решения.
5) Найти наибольшее значение параметра а , при котором уравнение имеет два корня.