Презентация на тему Параллелограмм Вариньона решает задачи

на практике с наименьшими временными затратами.


Задачи:
Изучить теоретический материал: понятия

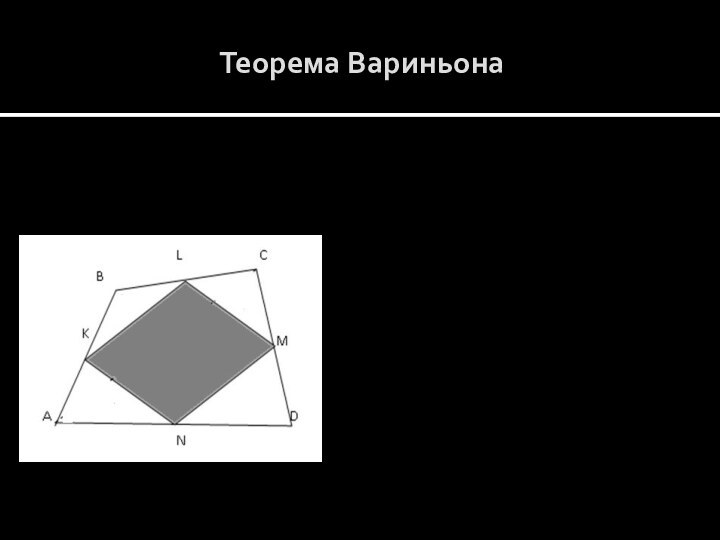
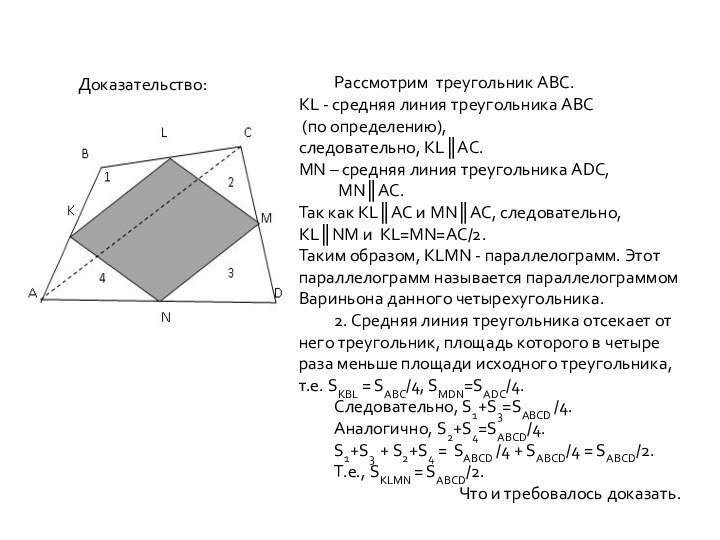
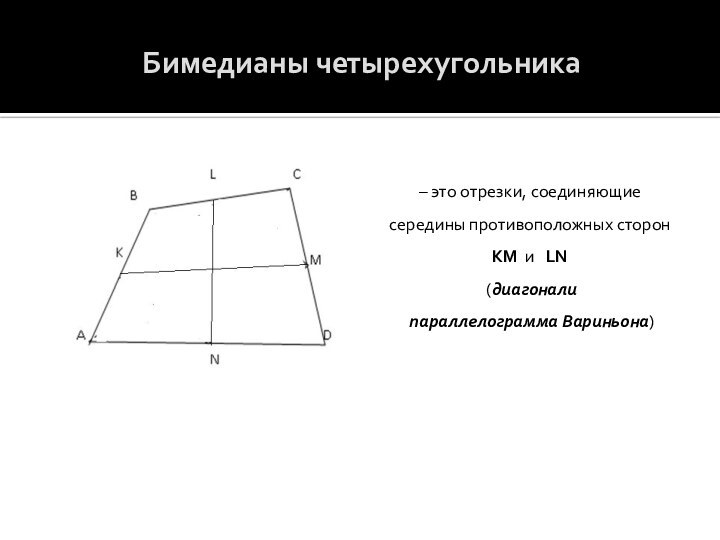
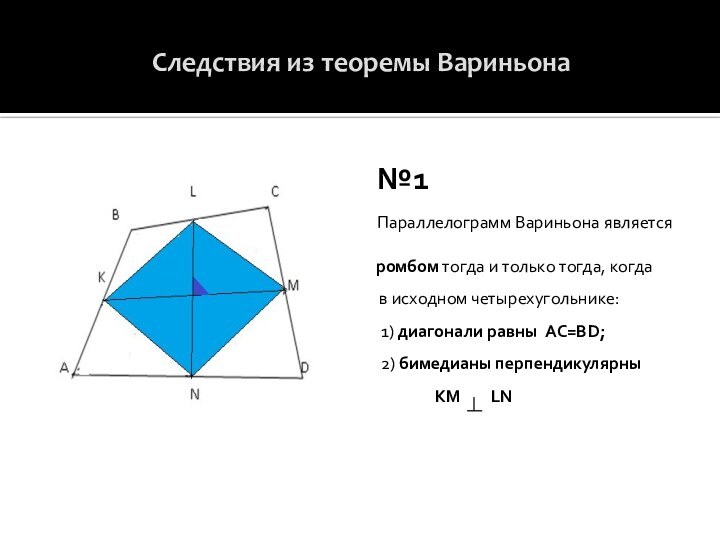
«параллелограмм Вариньона», бимедианы четырехугольника, разобрать доказательство теоремы Вариньона и следствия из нее.
Сравнить количество времени, необходимое для решения задач традиционным способом и, используя теорему Вариньона.
Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.

Написал учебник по элементарной геометрии (издан в 1731

году).
Первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Пьер Вариньон
(1654 – 1722)

выпуклого четырехугольника, является параллелограммом, и его площадь равна половине

площади данного четырехугольника.

Дано: ABCD – выпуклый четырехугольник, AK=KB, BL=LC, CM= MD, AN=ND

Доказать:
KLMN – параллелограмм;
SKLMN =SABCD /2

ABC (по определению), следовательно, KL║AC. MN – средняя линия треугольника

ADC,
MN║AC. Так как KL║AC и MN║AC, следовательно, KL║NM и KL=MN=AC/2. Таким образом, KLMN - параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.
2. Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника, т.е. SKBL = SABC/4, SMDN=SADС/4.
Следовательно, S1+S3=SABCD /4.
Аналогично, S2+S4=SABCD/4.
S1+S3 + S2+S4 = SABCD /4 + SABCD/4 = SABCD/2.
Т.е., SKLMN = SABCD/2. Что и требовалось доказать.

и LN
(диагонали параллелограмма Вариньона)

[1] В. Вавилов,

П. Красников. Бимедианы четырехугольника//Математика. 2006 - №22.

и только тогда, когда в исходном четырехугольнике:
1) диагонали

равны AC=BD;
2) бимедианы перпендикулярны KM LN

тогда, когда в исходном четырехугольнике:
1)

диагонали перпендикулярны; AC BD 2) бимедианы равны KM=LN

когда в исходном четырехугольнике:
1) диагонали равны

AC=BD и перпендикулярны AC BD;
2) бимедианы равны MK=NL и перпендикулярны MK NL

являются вершинами параллелограмма.

Дано: ABCD –

четырехугольник
AK=KB, BL=LC, CM=MD, AN=ND

Доказать: KLMN – параллелограмм

Доказательство:
Проведем АС и рассмотрим АВС
KL – средняя линия, следовательно KL II AC,
KL= AC/ 2 .
Рассмотрим ADC, NM – средняя линия, следовательно NM II AC, NM = AC/2
KL II AC, NM II AC, следовательно, KL II NM.
KL= AC/ 2, NM = AC/2, следовательно, KL=NM.
KLMN – параллелограмм (противоположные стороны равны и параллельны)

Новое доказательство:

KLMN – параллелограмм Вариньона ( по определению)

являются середины сторон прямоугольника

Дано: ABCD – прямоугольник, DE=EA,

AL=LB, BM=MC, DH=HC

Доказать: ELMH – ромб

Доказательство:
Проведем АС, рассмотрим треугольник АВС.
LM – средняя линия, значит LM II AC, LM =AC/2.
Рассмотрим треугольник ADC, EH- средняя линия , EH II AC, EH = AC/2.
LM II EH, LM=EH, следовательно,
ELMH –параллелограмм.
Проведем BD. Так как BD=AC ( диагонали прямоугольника равны), значит EL=LM
Следовательно, ELMH – ромб.

Новое доказательство:

ELMH – ромб ( по 1 следствию из теоремы Вариньона)

его площадь равна произведению средних линий.

Дано:
ABCD- четырехугольник АС=ВD
Доказать:
SABCD = KM * LN

А

В

C

D

K

N

M

L

Доказательство: KLMN – параллелограмм Вариньона. Так как AC= BD, параллелограмм Вариньона является ромбом. SKLMN =KM*LN /2 (площадь ромба равна половине произведения его диагоналей ).
SABCD = 2 SKLMN = KM * LN

параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и

параллельными его диагоналям, в два раза больше площади исходного четырехугольника

старое, чего мы не знаем» Лоренс Питер


Пьер Вариньон жил

в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.