- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проективные преобразования прямой и плоскости
Содержание
- 2. Цель – изучить проективные преобразования прямой и
- 3. Проективные преобразования прямойПроективным преобразованием прямой g называется
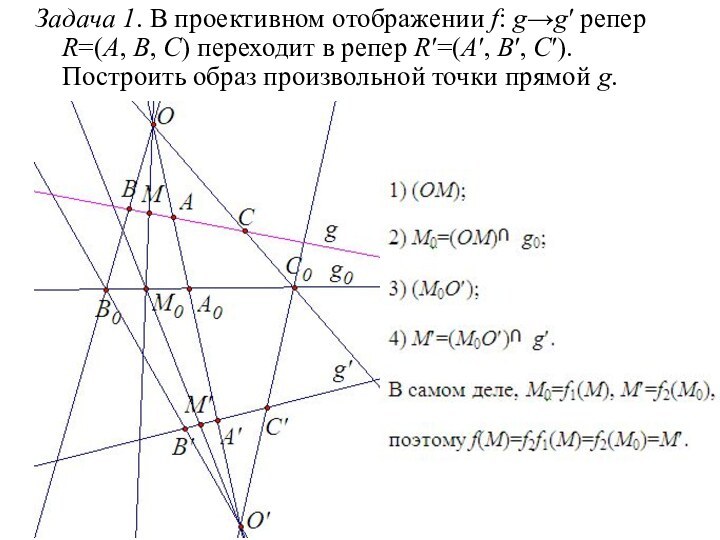
- 4. Задача 1. В проективном отображении f: g→g
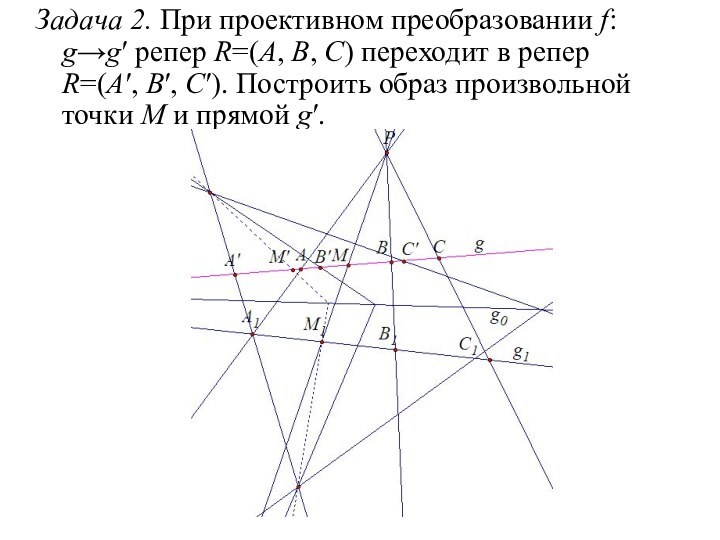
- 5. Задача 2. При проективном преобразовании f: g→g
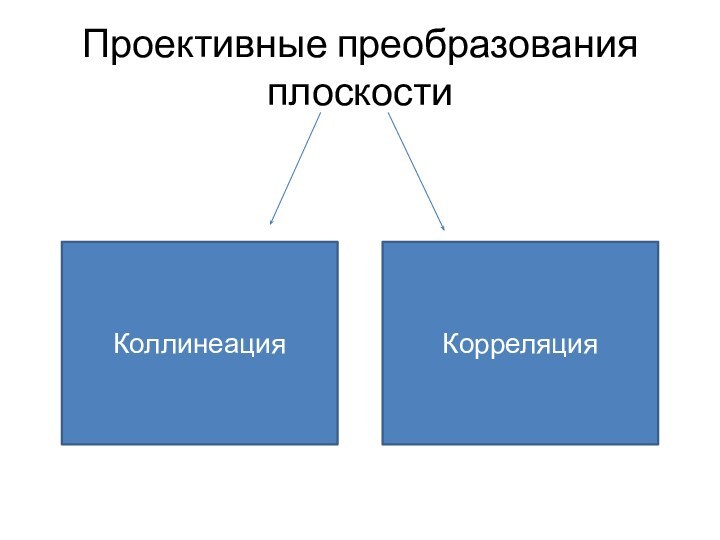
- 6. Проективные преобразования плоскостиКоллинеацияКорреляция
- 7. Проективные преобразования плоскостиКоллинеацияКорреляцияГомология
- 8. ГомологияГиперболическаяПараболическая
- 9. Скачать презентацию
- 10. Похожие презентации
Цель – изучить проективные преобразования прямой и плоскости. Задачи:1) Проанализировать литературу по теме;2) Выделить основные определения и теоремы;3) Привести задачи с решениями.