Слайд 2
Необходимые требования и навыки
Операции с векторами и матрицами.
Дифференциальное
и интегральное исчисление.
Случайные величины. Функция распределения, закон распределения случайной
величины Математическое ожидание, дисперсия, моменты распределения, ассиметрия, эксцесс.
Нормальное распределение.
Предельные теоремы и закон больших чисел.
Статистическое оценивание неизвестных параметров. Точные и интервальные оценки. Состоятельность, эффективность, несмещенность оценок.
Проверка статистических гипотез.
Дисперсионный анализ.
Слайд 3
Литература
Магнус Я. Р., Катышев П. К., Пересецкий А.
А. Эконометрика. Начальный курс. (любое издание).
Доугерти К. Введение в
эконометрику. Москва, 2001.
Эконометрика. Под ред. И. И. Елисеевой. Москва. Финансы и статистика, 2001.
Практикум по эконометрике. Под ред. И. И. Елисеевой. Москва, финансы и статистика, 2001
Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. Москва, Ю ЮНИТИ (любое издание).
Кремер Н. Ш., Путко Б. А. Эконометрика. М. ЮНИТИ, 2002
Слайд 4
Тема 1. Эконометрическое моделирование
Возникновение эконометрики как науки
Определение эконометрики
Прикладные
цели эконометрики
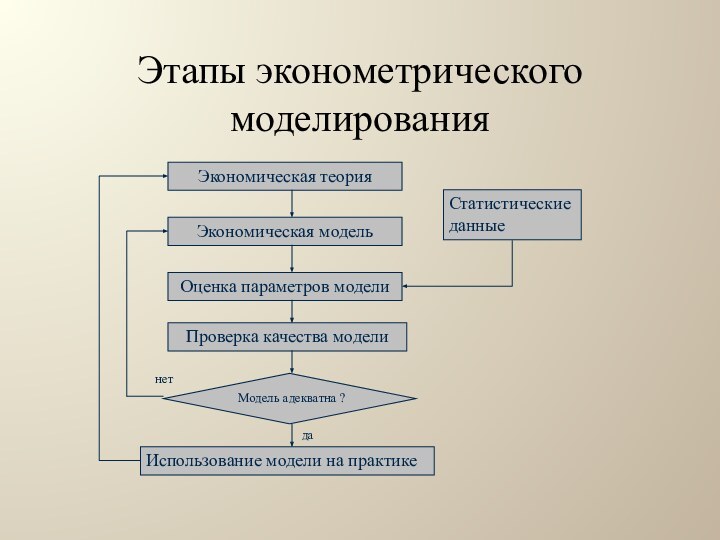
Этапы эконометрического моделирования
Слайд 5
История эконометрики как науки
1910, Австро-Венгрия – бухгалтер П.
Цьемпа ввел термин «эконометрика»
Цьемпа считал, что если к данным
бухгалтерского учета применить методы алгебры и геометрии, то будет получено новое, более глубокое представление о результатах хозяйственной деятельности.
Слайд 6
Современное определение эконометрики
Эконометрика – научная дисциплина, объединяющая совокупность
теоретических результатов, приемов, методов и моделей, предназначенных для того,
чтобы на базе
экономической теории;
экономической статистики;
математико-статистического инструментария
придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. (С. А. Айвазян, В. С. Мхитарян. Прикладная статистика и основы эконометрики.)
Слайд 7
Прикладные цели эконометрики
вывод экономических законов;
формулировка экономических моделей, основываясь
на экономической теории и эмпирических данных;
оценка неизвестных величин (параметров)
в этих моделях;
прогнозирование и оценка точности прогноза;
выработка рекомендаций по экономической политике.
Слайд 8
Этапы эконометрического моделирования
Осознание того факта, что в экономике
многие переменные связаны между собой
Группировка отдельных соотношений в модель
Сбор
данных
Идентификация
Верификация
Слайд 9
Этапы эконометрического моделирования
Слайд 10
1. Переменные модели
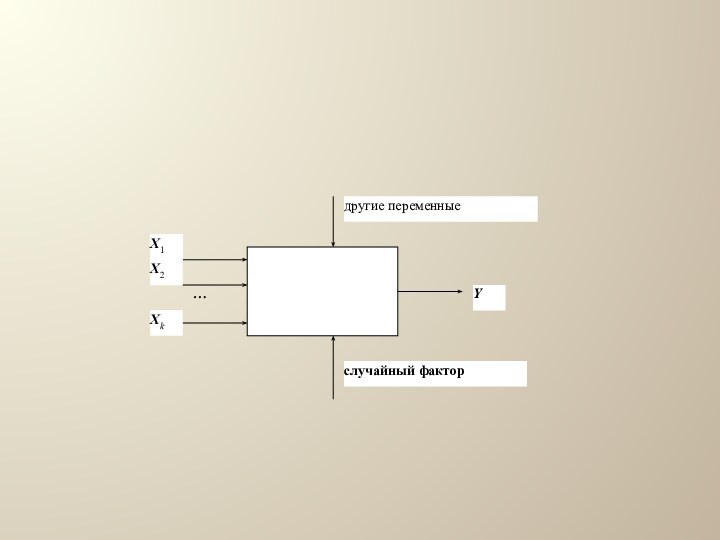
Переменную, процесс формирования значений которой нас
по каким-то причинам интересует, будем обозначать Y и называть
зависимой или объясняемой.
Переменные, которые, как мы предполагаем, оказывают влияние на переменную Y, будем обозначать Xj и называть независимыми или объясняющими.
Слайд 12
Другая классификация переменных
Переменные, значения которых объясняются в рамках
нашей модели, называются эндогенными.
Переменные, значения которых нашей моделью
не объясняются, являются для нее внешними, ничего о том, как формируются эти значения, мы не знаем, называются экзогенными
Слайд 13
2. Спецификация модели
определение цели моделирования;
определения списка экзогенных и
эндогенных переменных;
определение форм зависимостей между переменными;
формулировка априорных ограничений на
случайную составляющую, что важно для свойств оценок и выбора метода оценивания;
формулировка априорных ограничений на коэффициенты
Слайд 14
Виды эконометрических моделей
Модели временных рядов.
Регрессионные модели с одним
уравнением.
Системы одновременных уравнений.
Слайд 15
Модели временных рядов.
Такие модели объясняют поведение переменной, меняющейся
с течением времени, исходя только из ее предыдущих значений.
К этому классу относятся модели тренда, сезонности, тренда и сезонности (аддитивная и мультипликативная формы) и др.
Слайд 16
Регрессионные модели с одним уравнением.
В таких моделях зависимая
(объясняемая) переменная представляется в виде функции от независимых (объясняющих)
переменных и параметров. В зависимости от вида функции модели бывают линейными и нелинейными.
Слайд 17
Системы одновременных уравнений.
Ситуация экономическая, поведение экономического объекта описывается
системой уравнений. Системы состоят из уравнений и тождеств, которые
могут содержать в себе объясняемые переменные из других уравнений (поэтому вводят понятия экзогенных и эндогенных переменных).
Слайд 18
3. Сбор данных.
cross-sectional data – пространственные данные –
набор сведений по разным экономическим объектам в один и
тот же момент времени;
time-series data – временные ряды – наблюдение одного экономического параметра в разные периоды или моменты времени. Эти данные естественным образом упорядочены во времени.
panel data – панельные данные – набор сведений по разным экономическим объектам за несколько периодов времени (данные переписи населения).
Слайд 19
4. Идентификация.
Идентификация модели – статистический анализ модели
и, прежде всего – статистическое оценивание параметров. Выбор метода
оценивания сюда тоже входит. Зависит от особенностей модели.
Слайд 20
5. Верификация.
Верификация модели – сопоставление реальных и модельных
данных, проверка оцененной модели с тем, чтобы прийти к
выводу о достаточной реалистичности получаемой с ее помощью картины объекта, либо признать необходимость оценки другой спецификации модели.
Слайд 21
Вопросы для самопроверки
Кто первый ввел в употребление термин
«Эконометрика».
В каком году был основан журнал «Eсonometrics».
Каких вы знаете
лауреатов нобелевской премии по экономике за достижения в эконометрических методах.
На каких «трех китах» базируется современная экономическая теория.
Приведите определение эконометрики, отражающее современный взгляд на эту науку.
Каковы прикладные цели эконометрики.
Перечислите основные этапы эконометрического моделирования.
Что входит в спецификацию модели.
Что происходит на этапе идентификации модели.
Какие основные типы экономических данных вы знаете.
Основные типы эконометрических моделей.
Как происходит верификация модели
Слайд 22
Тема 2. Парная линейная регрессионная модель
ПЛРМ
Слайд 23
Две переменные X и Y
могут быть
связаны
функциональной зависимостью (т.е. существует функция f что Y
= f(X), значения переменной Y полностью определяются значениями переменной X)
статистической зависимостью
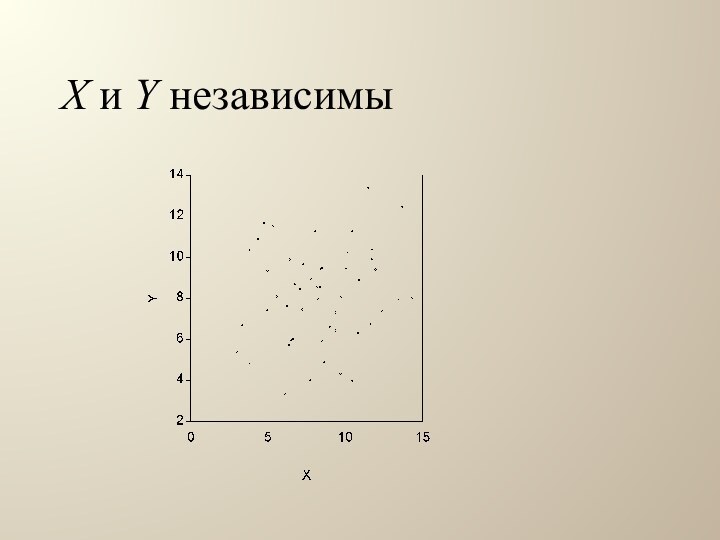
независимы.
Слайд 24
Статистическая зависимость
Если при изменении X меняется закон распределения
случайной величины Y, то говорят, что величины (X,Y) связаны
статистической зависимостью.
Статистическая зависимость называется корреляционной, если при изменении X меняется математическое ожидание случайной величины Y.
Слайд 25
Корреляционная зависимость
Если каждому значению величины X соответствует свое
значение
то говорят, что существует
регрессионная функция
Слайд 26
Случайная составляющая
Отклонение переменной Y от математического ожидания для
соответствующего значения переменной X называется ошибкой и обозначается
Слайд 27
Регрессионное уравнение
Уравнение
называется уравнением регрессии переменной Y на переменную
Слайд 28
Экономический смысл
невключение объясняющих переменных в уравнение. На
самом деле на переменную Y влияет не только переменная
X, но и ряд других переменных, которые не учтены в нашей модели по следующим причинам:
мы знаем, что другая переменная влияет, но не модем ее учесть, потому как не знаем, как измерить (психологический фактор, например);
существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать;
существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем.
Слайд 29
Экономический смысл (продолжение)
Неправильная функциональная спецификация. Функциональное соотношение
между Y и Х может быть определено неправильно. Например,
мы предположили линейную зависимость, а она может быть более сложной.
Ошибки наблюдений (занижение реального уровня доходов). В этом случае наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить свой вклад в остаточный член.
Слайд 30
Способы определения регрессионной функции f(X)
параметрический – предполагаем,
что вид регрессионной функции известен, неизвестны параметры функции
непараметрический –
предполагаем, что вид регрессионной функции неизвестен и мы составляем алгоритм расчета значений функции в каждой точке
Слайд 31
Выбор вида f(X)
экономическая теория
опыт, интуиция исследователя
эмпирический анализ данных
Слайд 32
Эмпирический анализ данных
В парном случае материал наблюдений представляет
собой набор пар чисел:
.
Слайд 33
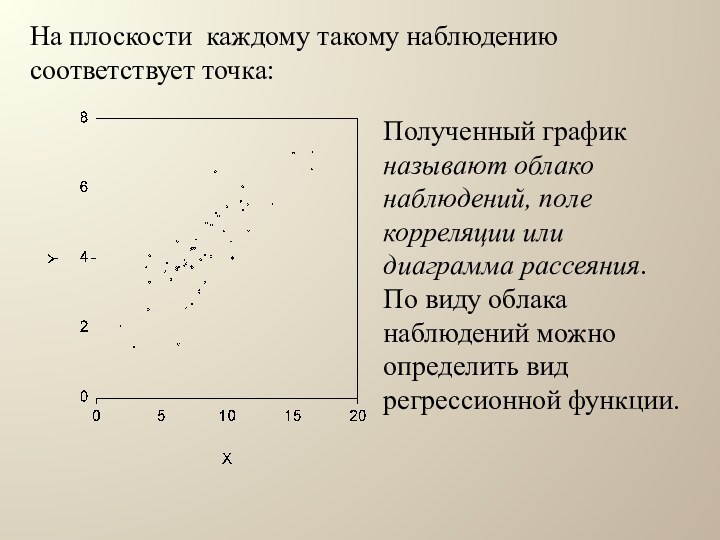
На плоскости каждому такому наблюдению соответствует точка:
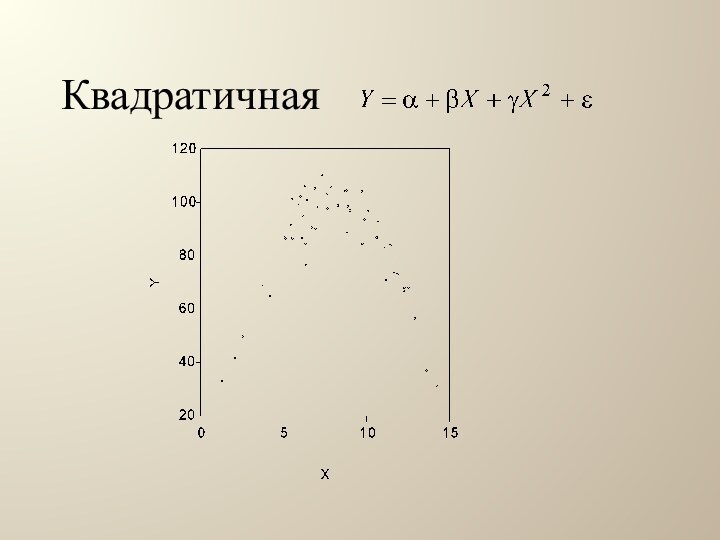
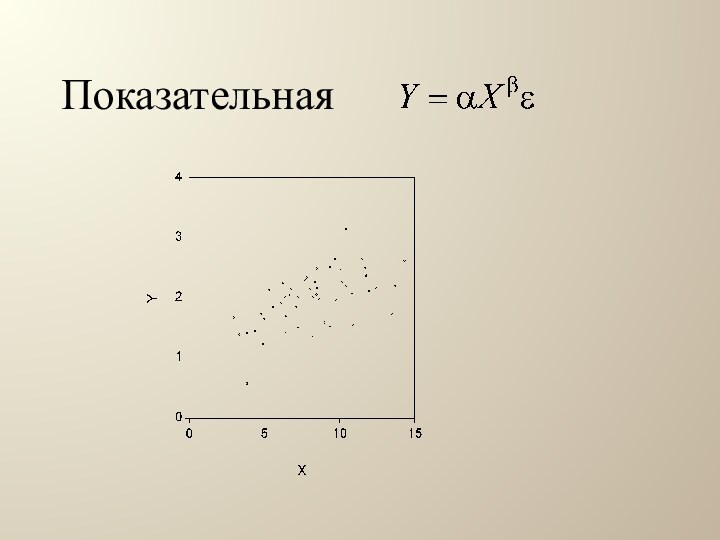
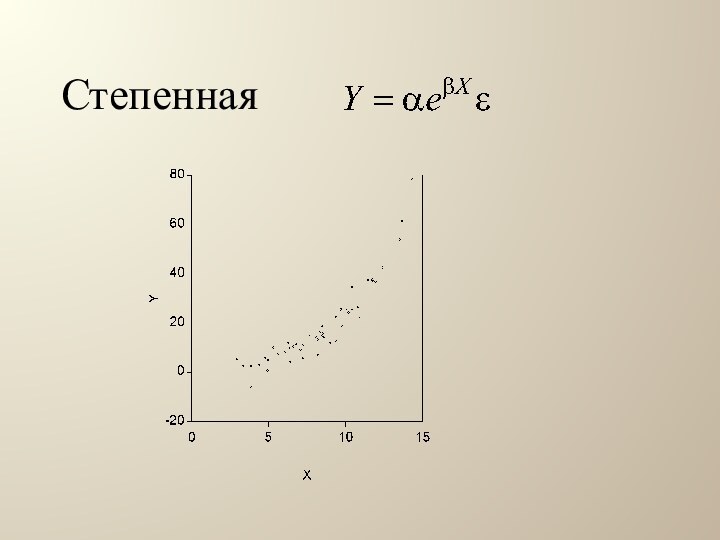
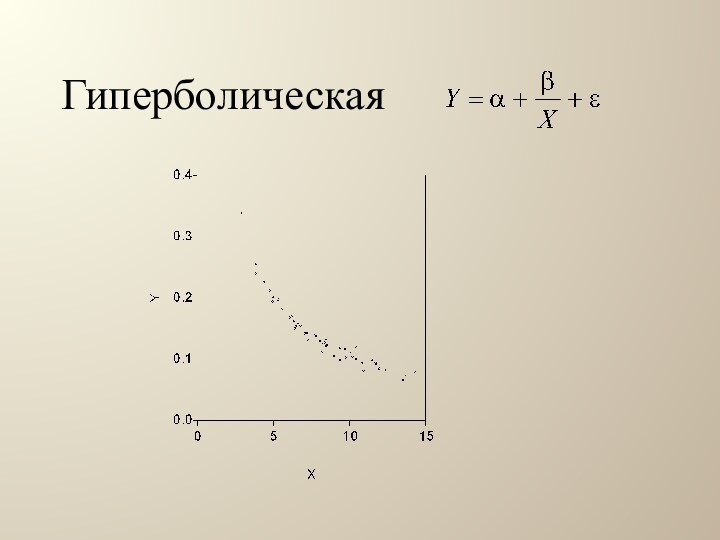
Полученный график
называют облако наблюдений, поле корреляции или диаграмма рассеяния. По
виду облака наблюдений можно определить вид регрессионной функции.
Слайд 40
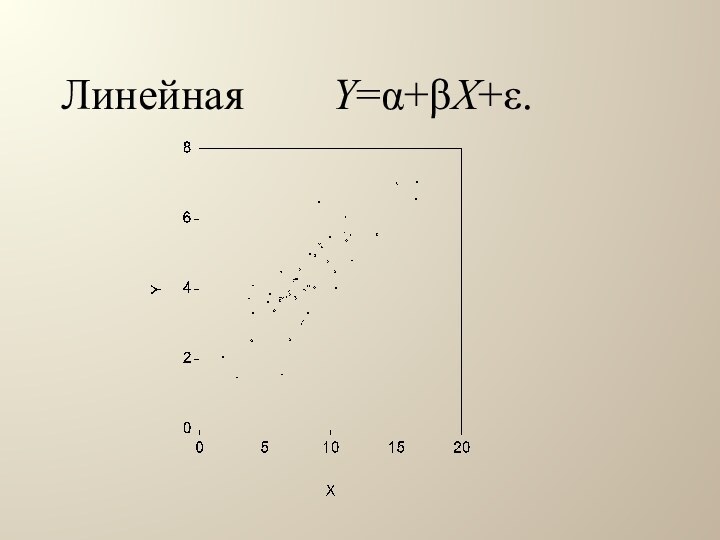
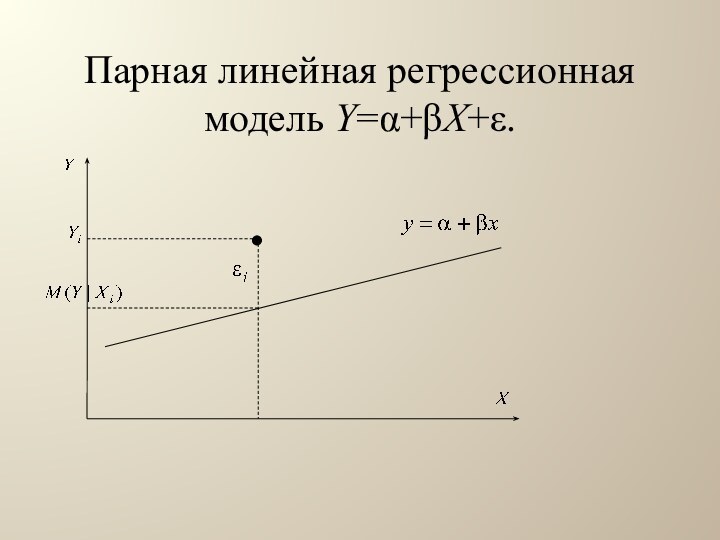
Парная линейная регрессионная модель Y=+X+.
Слайд 41
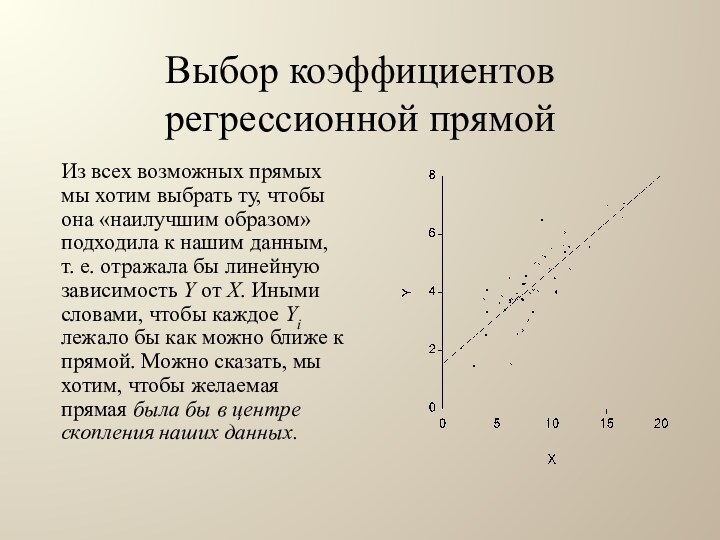
Выбор коэффициентов регрессионной прямой
Из всех возможных прямых мы
хотим выбрать ту, чтобы она «наилучшим образом» подходила к
нашим данным, т. е. отражала бы линейную зависимость Y от X. Иными словами, чтобы каждое Yi лежало бы как можно ближе к прямой. Можно сказать, мы хотим, чтобы желаемая прямая была бы в центре скопления наших данных.
Слайд 42
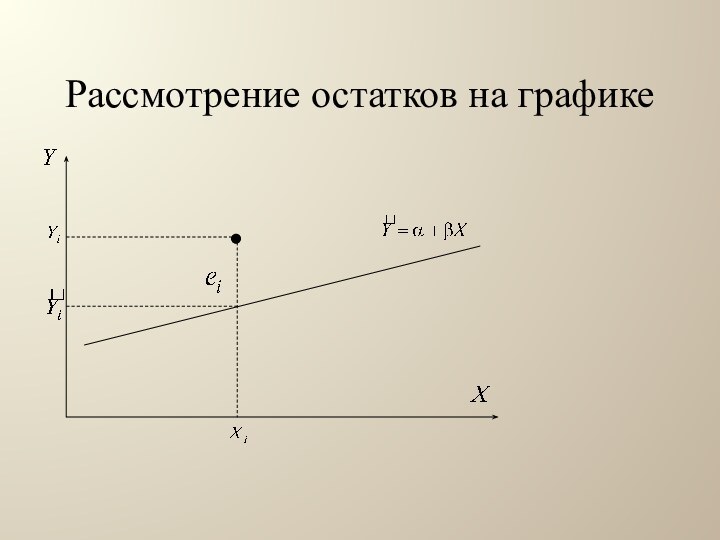
Рассмотрение остатков на графике
Слайд 44
Метод наименьших квадратов
Среди всех возможных прямых выбираем ту,
для которой сумма квадратов остатков минимальна
Слайд 47
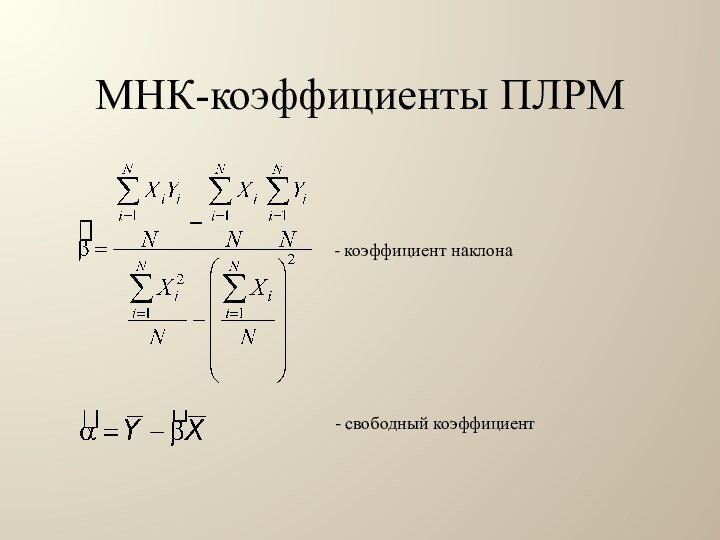
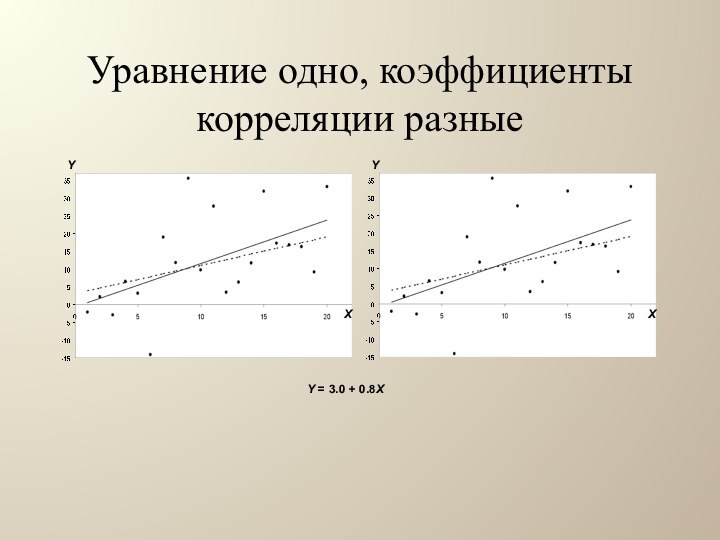
МНК-коэффициенты ПЛРМ
- коэффициент наклона
- свободный коэффициент
Слайд 48
Другие формы записи коэффициента наклона
Слайд 49
Замечания
Линия регрессии проходит через точку
Мы предполагаем, что
среди Xi есть разные, тогда X 0. В
противном случае, оценок по методу наименьших квадратов не существует.
Слайд 50
Теснота линейной корреляционной связи
В качестве меры близости данных
наблюдений к линии регрессии служит выборочный коэффициент парной линейной
корреляции (парный линейный коэффициент корреляции):
Слайд 51
Связь между коэффициентом корреляции и коэффициентом наклона
Знак коэффициента
наклона линии регрессии и коэффициента корреляции совпадают
Слайд 52
Свойства коэффициента корреляции
Если
- необходимое и
достаточное условием того, что все наблюдаемые значения (Xi,Yi) лежат на прямой регрессии
Слайд 53
Свойства коэффициента корреляции (продолжение)
переменные не связаны линейной корреляционной
связью. Линия регрессии проходит горизонтально.
между переменными существует линейная корреляционная
связь, которая тем лучше (ближе к линейной функциональной), чем ближе коэффициент корреляции по модулю к 1