- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ТЕМА 3. ОСНОВНЫЕ ВИДЫ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
Содержание
- 2. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫСлучайной величиной (СВ) называют величину,
- 3. ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИНДискретные – область значений счетнаяНепрерывные - область значений бесконечна
- 4. Распределением случайной величиныназывается закономерность встречаемости разных ее значений (Плохинский Н.А., 1970, с. 12).
- 5. ТИПЫ РАСПРЕДЕЛЕНИЙРавномерное распределение — когда все значения
- 6. ЗАКОН РАСПРЕДЕЛЕНИЯ СВ (табличная форма)
- 7. ЗАКОН РАСПРЕДЕЛЕНИЯ СВ (аналитическая форма)
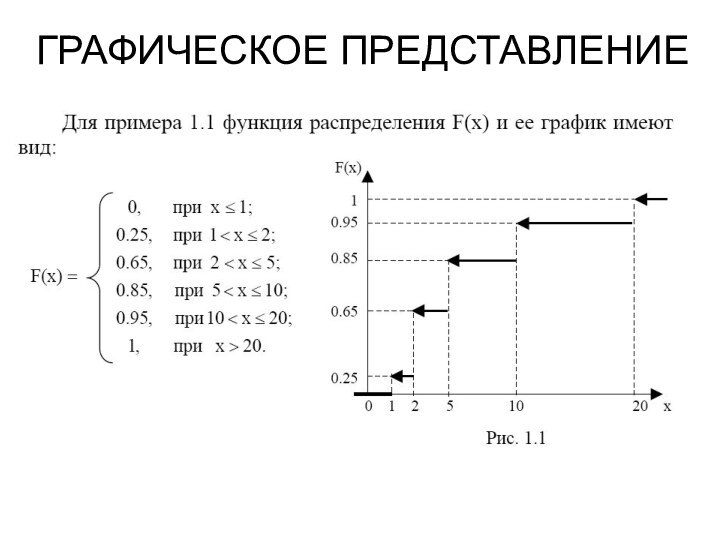
- 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
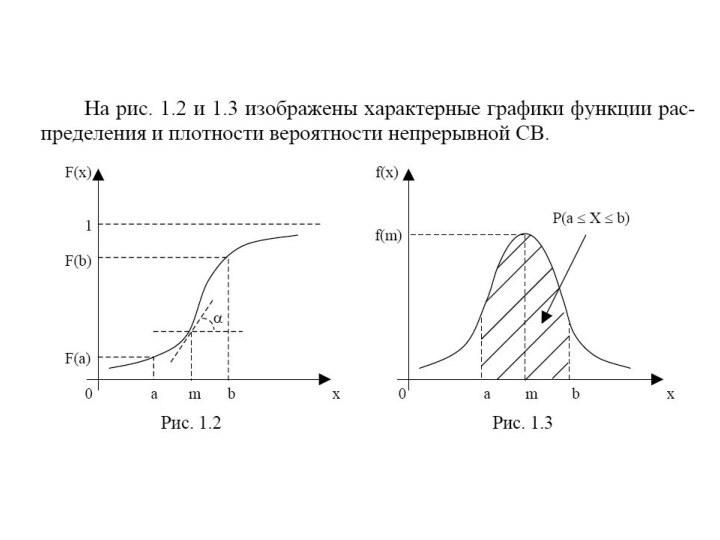
- 10. НЕПРЕРЫВНАЯ СВ
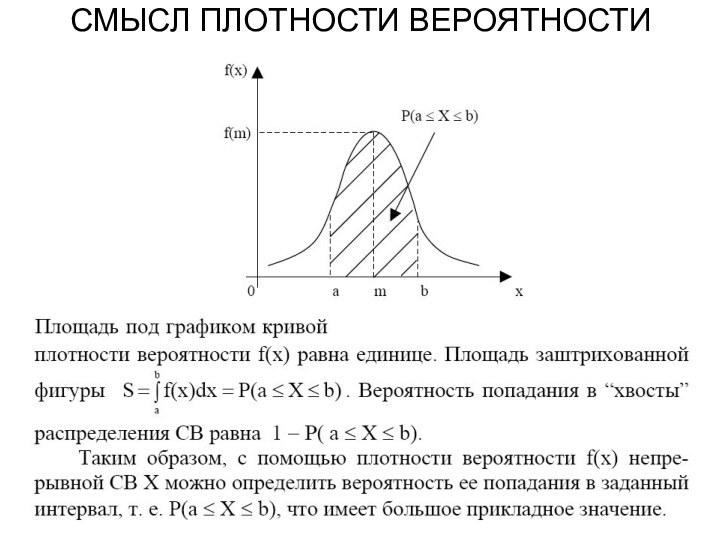
- 14. СМЫСЛ ПЛОТНОСТИ ВЕРОЯТНОСТИ
- 15. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СВ
- 16. Параметры распределения- это его числовые характеристики, указывающие,
- 22. Пример расчета характеристик дискретной случайной величины
- 24. ПРИМЕР 2
- 25. ПРИМЕР 3
- 29. ПРИМЕР 4
- 30. Пример биноминального распределения
- 31. Геометрическое распределение
- 32. Гипергеометрическое распределение
- 33. Пуассоновское распределение
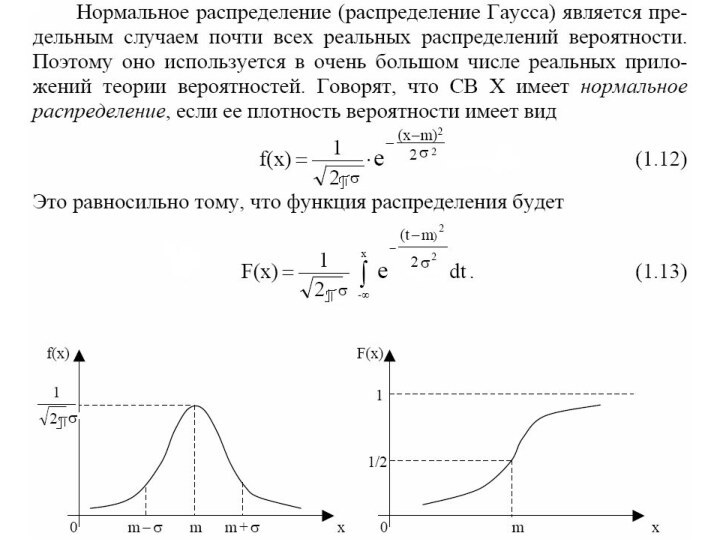
- 34. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ -НОРМАЛЬНОЕНормальным распределение называется потому, что
- 36. Методы проверки распределения на нормальность 1. Визуальный
- 41. Визуальный метод
- 42. Асимметрией (Skewness)или выборочным коэффициентом скошенности, называют меру
- 43. АССИМЕТРИЯЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, то они имеют симметричное распределение признака, когда As=0
- 44. Показатель эксцесса (Kurtosis)или выборочный коэффициент остро вершинности
- 45. ЭКСЦЕСС («горб»)ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, то они имеют такой «горб», когда Ех=0
- 47. НОРМАЛЬНЫЕ ДАННЫЕ правило трех сигм ЕСЛИ В СОВОКУПНОСТИ ВСЕ ВАРИАНТЫ НАХОДЯТСЯ В ИНТЕРВАЛЕ , ТО ОНИ НОРМАЛЬНЫЕ
- 48. АНОМАЛЬНЫЕ ДАННЫЕ ВЫБРОСЫ ЕСЛИ В СОВОКУПНОСТИ ЕСТЬ ВАРИАНТЫ, КОТОРЫЕ НАХОДЯТСЯ ЗА ПРЕДЕЛАМИ ИНТЕРВАЛА , ТО ОНИ АНОМАЛЬНЫЕ
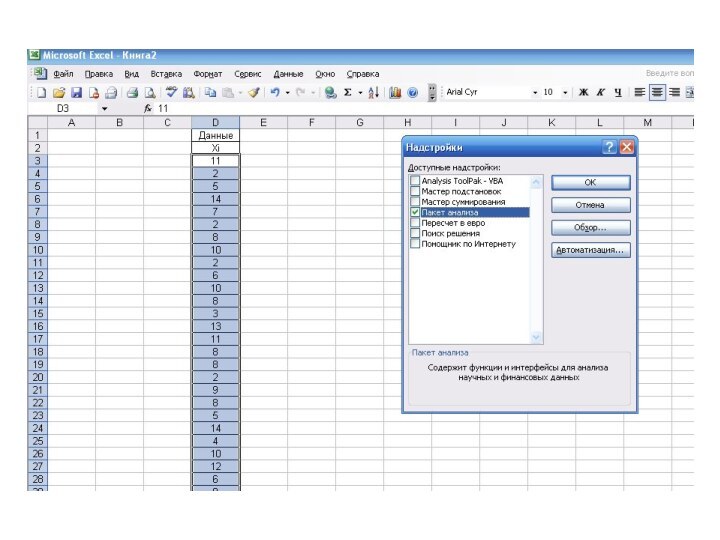
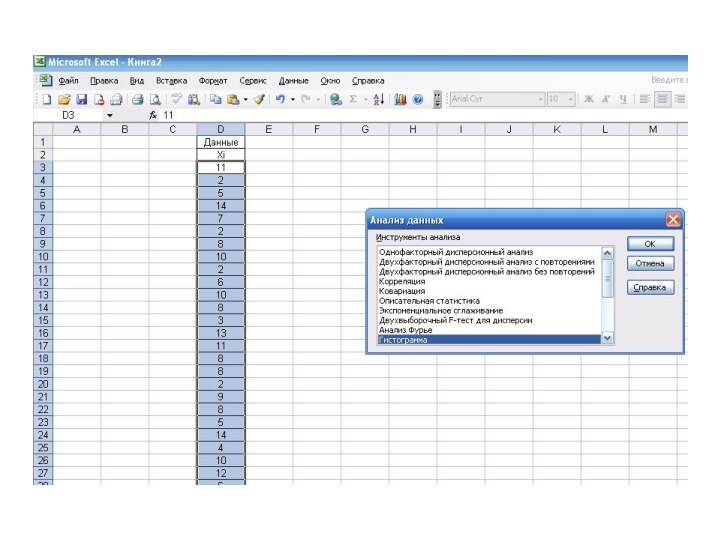
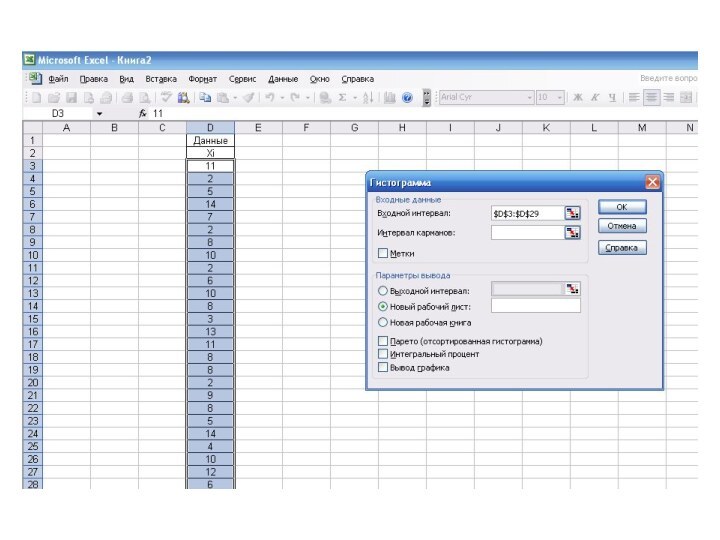
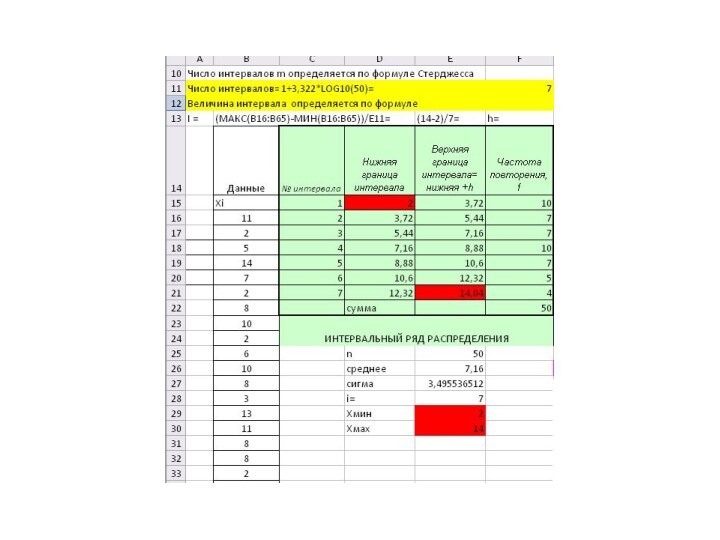
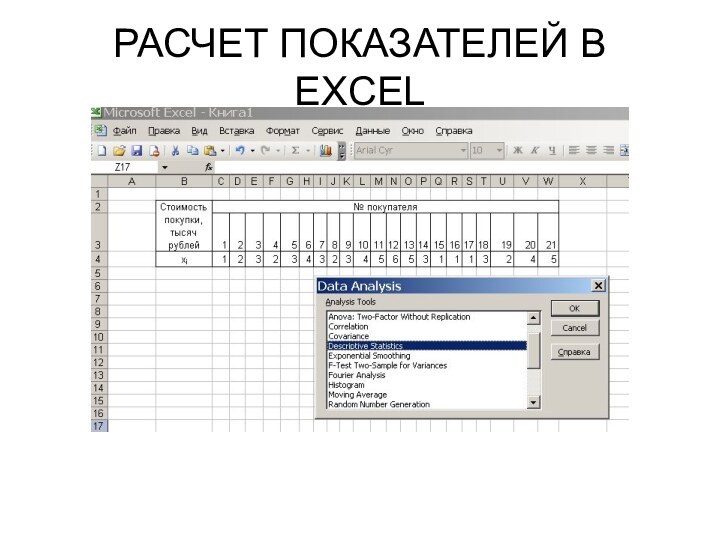
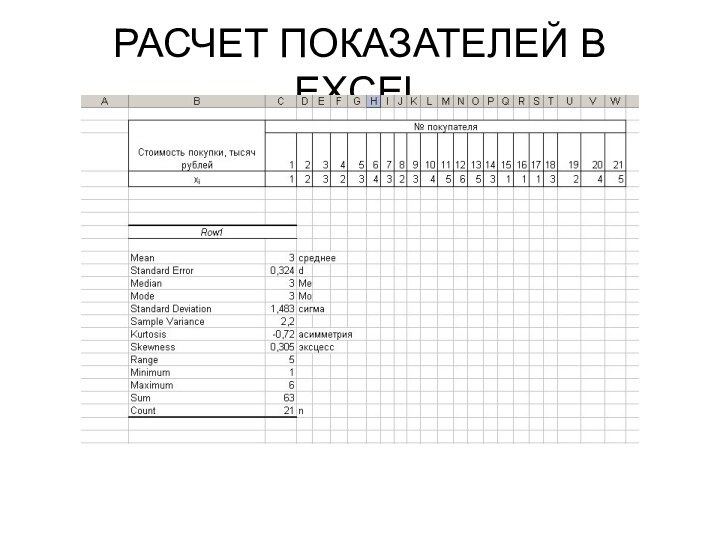
- 49. РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL
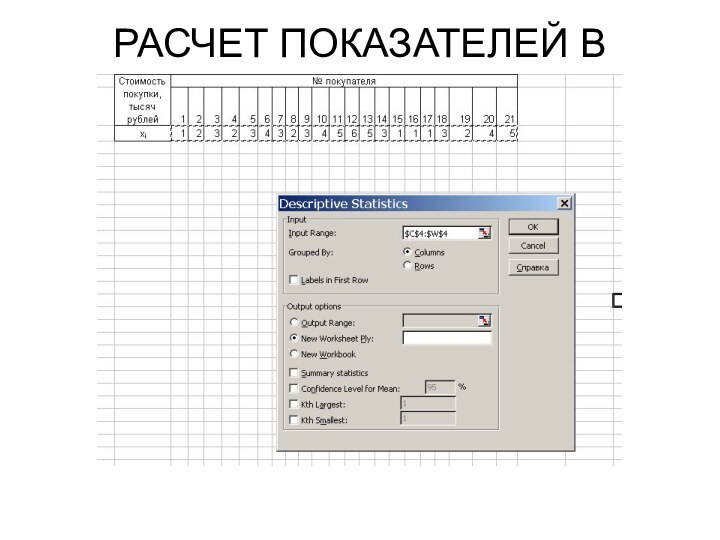
- 50. РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL
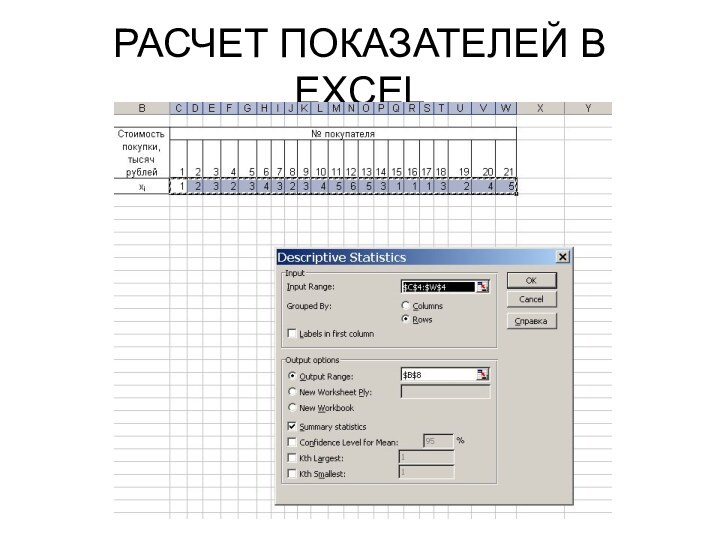
- 51. РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL
- 52. РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL
- 53. РАСЧЕТ ПОКАЗАТЕЛЕЙ В EXCEL
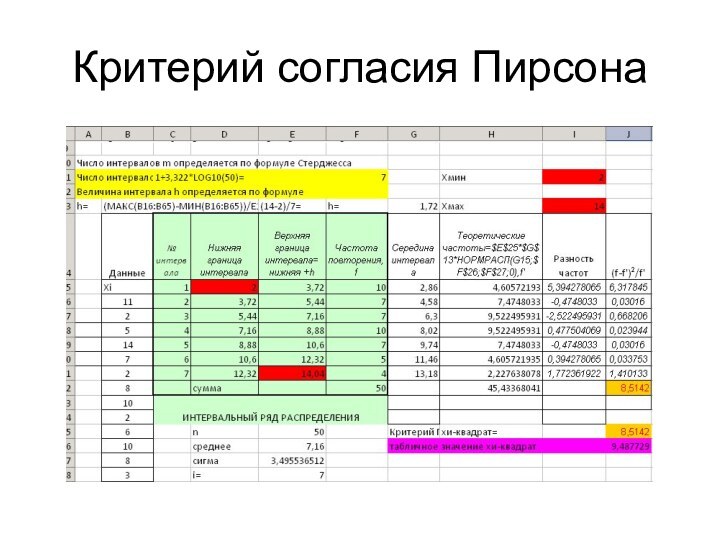
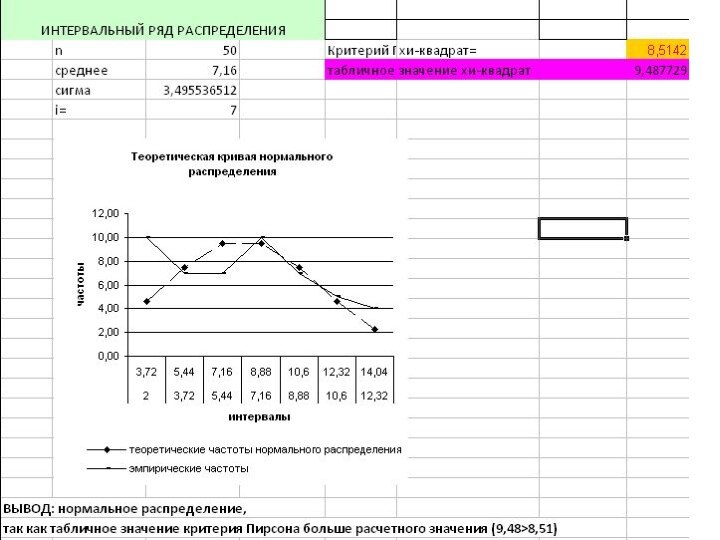
- 54. Критерий согласия Пирсона
- 56. ПРИМЕНЕНИЕ СВ
- 57. ПОЧЕМУ РАСПРЕДЕЛЕНИЕ ГАУССА ГЛАВНОЕ?1. Оно является предельным
- 58. ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ В EXCELНОРМРАСП(х; среднее;σ;интегральная)Если интегральная
- 60. ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ В EXCELНОРМОБР(вероятность, среднее, σ)
- 65. Скачать презентацию
- 66. Похожие презентации
ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫСлучайной величиной (СВ) называют величину, которая в результате наблюдения принимает то или иное значение, заранее неизвестное и зависящее от случайных обстоятельств с определенной вероятностью
Слайд 3
ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Дискретные – область значений счетная
Непрерывные -
область значений бесконечна
Слайд 4
Распределением случайной величины
называется закономерность встречаемости разных ее значений
(Плохинский Н.А., 1970, с. 12).
Слайд 5
ТИПЫ РАСПРЕДЕЛЕНИЙ
Равномерное распределение — когда все значения встречаются
одинаково (или почти одинаково) часто.
Симметричное распределение — когда
одинаково часто встречаются крайние значения. Нормальное распределение — симметричное распределение, у которого крайние значения встречаются редко и частота постепенно повышается от крайних к серединным значениям признака.
Асимметричные распределения — левосторонние (с преобладанием частот малых значений), правосторонние (с преобладанием частот больших значений).
Слайд 16
Параметры распределения
- это его числовые характеристики, указывающие, где
"в среднем" располагаются значения признака, насколько эти значения изменчивы
и наблюдается ли преимущественное появление определенных значений признака.Наиболее практически важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса.
Параметры распределения оказывается возможным определить только по отношению к данным, представленным по крайней мере в интервальной шкале.
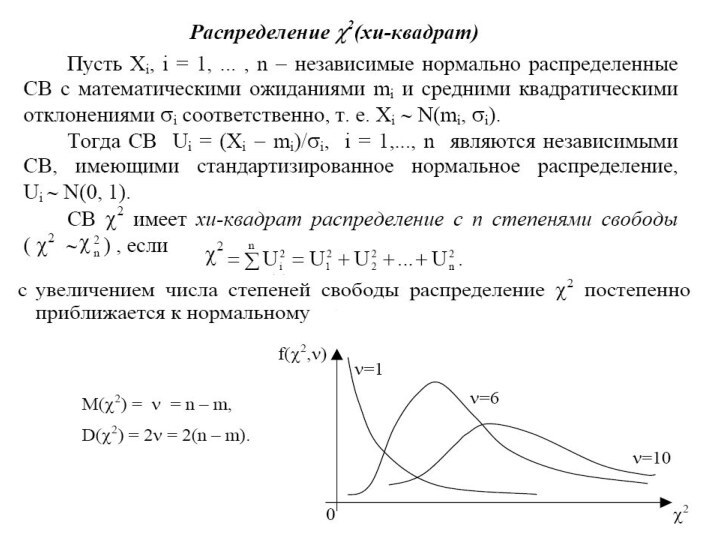
Слайд 34
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ -НОРМАЛЬНОЕ
Нормальным распределение называется потому, что оно
очень часто встречалось в естественно-научных исследованиях и казалось "нормой"
всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции. График нормального распределения представляет собой привычную глазу психолога-исследователя так называемую колоколообразную кривую.
Слайд 36
Методы проверки распределения на нормальность
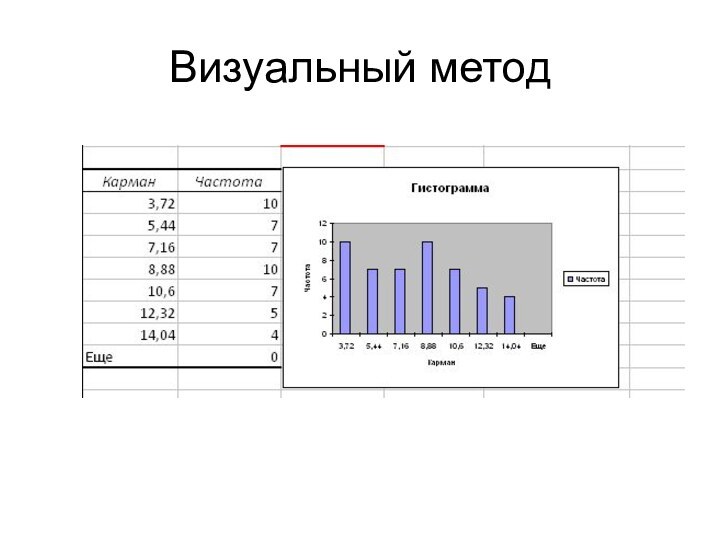
1. Визуальный метод
включает построение гистограммы эмпирического распределения (такая возможность реализована во
всех популярных статистических пакетах) и ее визуальное сравнение с теоретической кривой нормального распределения.2. Метод оценки показателей асимметрии и эксцесса основан на вычислении этих показателей и их стандартных ошибок.
3. Критерии согласия
Слайд 42
Асимметрией (Skewness)
или выборочным коэффициентом скошенности, называют меру отклонения
эмпирического распределения частот от распределения, симметричного относительно максимальной ординаты.
Для
симметричных распределений показатель асимметрии равен нулю. Отрицательный показатель асимметрии означает, что кривая распределения скошена влево, положительный – вправо от теоретической симметричной кривой распределения.
Слайд 43
АССИМЕТРИЯ
ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, то они имеют симметричное распределение
признака, когда As=0
Слайд 44
Показатель эксцесса (Kurtosis)
или выборочный коэффициент остро вершинности характеризует
степень отклонения эмпирической кривой распределения от теоретической кривой нормального
распределения
Слайд 47
НОРМАЛЬНЫЕ ДАННЫЕ
правило трех сигм
ЕСЛИ В СОВОКУПНОСТИ ВСЕ ВАРИАНТЫ
НАХОДЯТСЯ В ИНТЕРВАЛЕ , ТО ОНИ НОРМАЛЬНЫЕ
Слайд 48
АНОМАЛЬНЫЕ ДАННЫЕ
ВЫБРОСЫ
ЕСЛИ В СОВОКУПНОСТИ ЕСТЬ ВАРИАНТЫ, КОТОРЫЕ НАХОДЯТСЯ
ЗА ПРЕДЕЛАМИ ИНТЕРВАЛА , ТО ОНИ АНОМАЛЬНЫЕ
Слайд 57
ПОЧЕМУ РАСПРЕДЕЛЕНИЕ ГАУССА ГЛАВНОЕ?
1. Оно является предельным законом,
к которому приближаются другие законы при росте числа степеней
свободы.2. ЗБЧ доказывают, что сумма достаточно большого числа независимых случайных величин, подчиненных каким-либо законам распределения, приближенно подчиняется нормальному закону, и это тем точнее, чем больше количество случайных величин суммируется, каждая величин в сумме должна играть малую роль.
3. Оно используется, если СВ имеет закон распределения другой, но вычисления по нему сложны, а аппроксимация его нормальным распределением допустима.
Слайд 58
ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ В EXCEL
НОРМРАСП(х; среднее;σ;интегральная)
Если интегральная равна
Ложь(0), то вычисляется плотность распределения, если Истина, то функция
нормального распределения
Слайд 60
ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ В EXCEL
НОРМОБР(вероятность, среднее, σ) –
