Слайд 2
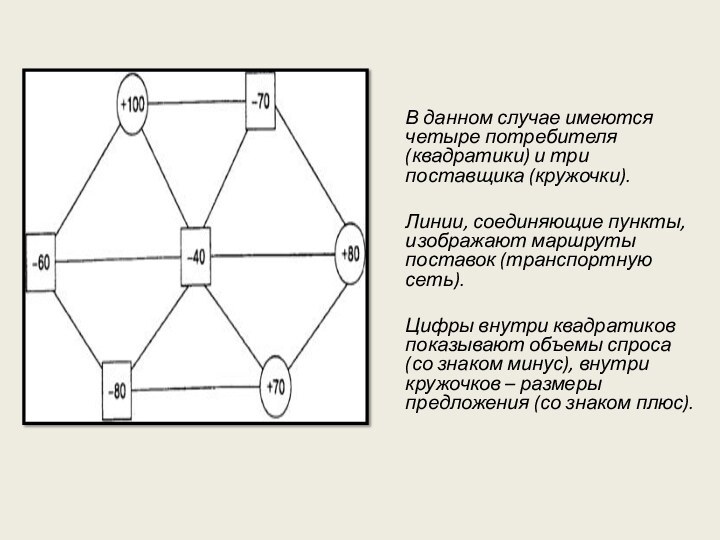
В данном случае имеются четыре потребителя (квадратики) и
три поставщика (кружочки).
Линии, соединяющие пункты, изображают маршруты поставок
(транспортную сеть).
Цифры внутри квадратиков показывают объемы спроса (со знаком минус), внутри кружочков – размеры предложения (со знаком плюс).
Слайд 3
Даже коты довольны транспортной задачей.
Теперь их корм
стоит дешевле.
Слайд 4
Задача об оптимальном использовании ресурсов при производственном планировании
Предприятие
выпускает n различных изделий. Для их производства требуется m
различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, B1, B2,..., Bm условных единиц.
Известны также технологические коэффициенты aij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида.
Прибыль, получаемая предприятием при реализации изделия j-го вида, равна Cj.
В планируемом периоде значения величин Aij, Bi и Cj остаются постоянными
Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей.
Слайд 5
Компания специализируется на выпуске хоккейных клюшек и наборов
шахмат. Каждая клюшка приносит компании прибыль в размере 2$,
а каждый шахматный набор - в размере 4$.
На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B.
Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C.
Доступная производственная мощность участка A составляет 120 н-часов в день, участка В - 72 н-часа и участка С - 10 н-часов.
Слайд 6
Задача о назначениях
Распределяется заказ (загрузки взаимозаменяемых групп оборудования)
между предприятиями (цехами, станками, исполнителями) с различными производственными и
технологическими характеристиками, но взаимозаменяемыми в смысле выполнения заказа.
Требуется составить план размещения заказа (загрузки оборудования), при котором с имеющимися производственными возможностями заказ был бы выполнен, а показатель эффективности достигал экстремального значения.
Слайд 7
В цехе предприятия имеются 5 универсальных станков, которые
могут выполнять 4 вида работ. Каждую работу единовременно может
выполнять только один станок, и каждый станок можно загружать только одной работой.
Даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.
Служба занятости имеет в наличии четыре вакантных места по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в некоторой матрице
Распределить претендентов на вакантные места таким образом, чтобы на каждое место был назначен человек с наибольшим набранным по тестированию баллом.
Слайд 8
Задача о раскрое материалов
Сущность задачи об
оптимальном раскрое состоит в разработке таких технологически допустимых планов
раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму.
Рассматривается простейшая модель раскроя по одному измерению. Более сложные постановки ведут к задачам целочисленного программирования.
Слайд 9
На швейной фабрике ткань может быть раскроена несколькими
способами для изготовления нужных деталей швейных изделий. Пусть при
j-м варианте раскроя 100 м₂ ткани изготовляется Bij деталей i-го вида , а величина отходов при данном варианте раскроя равна Сj м₂.
Зная, что деталей i-го вида следует изготовлять Bi штук, требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах.
Слайд 10
Задача о рюкзаке
Имеется набор предметов, каждый с
определенным весом и определенной стоимостью.
Из этого набора необходимо
выбрать предметы с максимальной стоимостью, с учетом ограничения на максимальный вес (вес «рюкзака»).