Слайд 2
Модели оценки стоимости финансовых активов
Базовая модель оценки
стоимости финансовых активов
(DCF-модель):
Vo =
где CFt — ожидаемый
денежный поток в t-м периоде;
d — приемлемая (ожидаемая или требуемая) доходность;
n — число периодов, включенных в расчет.
DCF-модель предполагает капитализацию дохода с доходностью, равной ставке дисконтирования. Для разных инвесторов V0 может иметь разные значения, т.к. по-разному оцениваются поступления денежных средств, приемлемая норма доходности.
Приемлемая норма доходности (d) может быть принята в размере:
• ставки процента по банковскому депозиту;
• ставки процента, выплачиваемого по вкладам, плюс надбавка за риск;
• процента, выплачиваемого по государственным ценным бумагам, плюс надбавка за риск.
Слайд 3
Модели оценки облигаций
Оценка облигаций с нулевым купоном
(облигаций, по которым поступления денежных средств по годам, за
исключением последнего, равны нулю) :
где Vo — стоимость облигации с позиции инвестора (теоретическая стоимость);
CF — сумма, выплачиваемая при погашении облигации;
n — число лет, через которое произойдет погашение облигации;
d — приемлемая (ожидаемая или требуемая) доходность
I — доход в абсолютном выражении;
N— номинальная стоимость облигации, подлежащая погашению в конце срока
Слайд 4
Модели оценки облигаций
Пример:
Облигация с нулевым купоном нарицательной
стоимостью 1000 руб. и сроком погашения 5 лет продается
за 630,12 руб. Проанализировать целесообразность приобретения этих облигаций на основе показателя внутренней (теоретической) стоимости, если имеется возможность альтернативного инвестирования с нормой прибыли в 12%.
Решение:
Реальная цена, по которой продается облигация (630,12 руб.), завышена относительно ее внутренней (теоретической) стоимости (567,43 руб.), поэтому ее покупка нецелесообразна.
Слайд 5
Модели оценки облигаций
Оценка бессрочных облигаций (облигаций, долговая
выплата по которым производится в установленном проценте или по
плавающей ставке) осуществляется по формуле:
где СF — ежегодная сумма дохода, выплачиваемая по облигации;
d — требуемая доходность инвестируемого капитала.
Пример:
Вычислить теоретическую стоимость бессрочной облигации, если выплачиваемый по ней годовой доход составляет 1000 руб., а рыночная приемлемая норма прибыли — 18%. При каком условии инвестирование средств в эти облигации эффективно.
Решение:
Если рыночная цена облигации больше чем 5555,56 руб., инвестирование средств в облигации не имеет смысла.
Слайд 6
Оценка безотзывных облигаций с постоянным доходом (облигаций, денежный
поток которых складывается из одинаковых по годам поступлений и
нарицательной стоимости в момент погашения)
— при годовом начислении процентов
— при полугодовом начислении процентов
где Ik — годовой купонный доход;
N — нарицательная стоимость, выплачиваемая при погашении облигации;
d — требуемая доходность инвестируемого капитала;
n — число лет до погашения облигаций;
k — число раз начисления процентов.
Оценка отзывных облигаций с постоянным доходом производится по данным формулам, в которых нарицательная стоимость N заменена выкупной ценой Рm.
Модели оценки облигаций
Слайд 7
Пример:
Рассчитать рыночную цену облигации нарицательной стоимостью 1000
руб. с купонной ставкой 15% годовых и сроком погашения
через четыре года, если рыночная норма прибыли по финансовому инструменту такого рода равна 10%. Процент по облигации выплачивается дважды в год.
Модели оценки облигаций
Слайд 8
Модели оценки стоимости акций
Оценка стоимости акции, используемой в
течение заранее неопределенного срока, производится по формуле:
Va
=
где Va — внутренняя или теоретическая стоимость акции с позиции инвестора, выполняющего анализ (субъективная оценка инвестором ожидаемого потока и рискованность акции);
Dt — сумма дивидендов, предполагаемая к получению в каждом t периоде;
ds — текущая требуемая доходность.
Слайд 9
Модели оценки стоимости акций
Для оценки стоимости акции, используемой
в течение заранее определенного срока, используется формула:
где Dt
— сумма дивидендов, предполагаемая к получению в каждом t периоде;
Pm — ожидаемая курсовая стоимость акции в конце периода ее использования;
ds — текущая требуемая доходность;
n — число периодов, включенных в расчет.
Слайд 10
Пример: Определить теоретическую стоимость акции, если известно, что
предполагаемый дивиденд по ней составляет 2 руб., акцию планируется
продать через 5 лет по цене 20 руб., требуемая текущая доходность равна 12%.
Решение:
Модели оценки стоимости акций
Слайд 11
Модели оценки стоимости акций
Оценка стоимости акции со стабильным
уровнем дивиденда (привилегированных акций) производится по формуле:
где Va —
текущая цена привилегированной акции;
D — ожидаемый фиксированный дивиденд;
ds—текущая требуемая доходность.
Пример
Привилегированная акция номиналом 25 руб. выпущена со ставкой фиксированного дивиденда 30% годовых. Требуемый уровень доходности данной акции, соответствующий ее риску, составляет 35% годовых в рублях. По какому курсу будет продаваться данная акция?
Решение:
D = 25 * 0,3 = 7,5 руб.
Слайд 12
Модели оценки стоимости акций
Для оценки стоимости акций с
равномерно возрастающим дивидендом используется формула:
где Va — внутренняя
или теоретическая стоимость акции с позиции инвестора, выполняющего анализ (субъективная оценка инвестором ожидаемого потока и рискованность акции);
Di — дивиденд, ожидаемый к получению (Di= D0*(1+ ),
где D0 — последний фактически выплаченный дивиденд);
ds — требуемая доходность акции, учитывающая как риск, так доходность альтернативных вариантов инвестирования;
— предполагаемый темп прироста дивиденда.
Равномерный рост дивидендов означает, что:
• доходы корпорации так же равномерно увеличиваются;
• доля прибыли, выплачиваемая в виде дивидендов, остается постоянной.
Слайд 13
Модели оценки стоимости акций
Пример:
Темп роста дивиденда по
акции российской компании А за прошлые годы составляет:
g
1 12 %
g 2 8 %
g 3 20 %
g 4 12 %
g 5 10 %
g 6 22 %
Дивиденд, ожидаемый в текущем периоде, равен 0,35 руб. за акцию. Оцените курс акции, если требуемый уровень ее доходности составляет, по рыночным данным, 23% годовых.
Решение:
Слайд 14
Доходность финансового актива
Доходность финансового актива — это
относительный показатель, характеризующий эффективность использования финансовых активов.
Исходная формула
расчета доходности :
где d — доход, генерируемый активом (дивиденд, процент, прирост капитализированной стоимости);
I — регулярный доход от использования актива, полученный в виде процентов или дивидендов;
CI — величина инвестиций в актив.
Показатели доходности:
• Фактическая доходность, рассчитываемая на основе фактически полученных данных и имеющая значение лишь для ретроспективного анализа.
• Ожидаемая доходность, рассчитываемая на основе прогнозных данных в рамках имитационного перспективного анализа и используемая для принятия решения о целесообразности приобретения тех или иных ценных бумаг.
Слайд 15
Доходность финансового актива
Алгоритм расчета доходности актива может
представлен следующим образом:
где dt — общая доходность;
ds
— текущая доходность;
dc— капитализированная доходность;
P0— цена приобретения актива;
Pm — ожидаемая цена реализации актива;
I — регулярный доход от использования актива, полученный в виде процентов или дивидендов.
Пример:
Предприниматель год назад приобрел акцию предприятия по цене 15 руб. Рыночная цена акции на текущий момент равна 16,7 руб., дивиденды по акции за год составили 1 руб. Определить общую доходность актива для предпринимателя.
Решение:
Слайд 16
Доходность облигаций
Доходность облигации без права
досрочного погашения (YTM) (доходность к погашению) определяется по формуле:
где N— номинал облигации;
P0 — текущая цена (на момент оценки);
Ik — купонный доход;
t — число лет, оставшихся до погашения облигации.
Слайд 17
Пример:
Рассчитать доходность облигации нарицательной стоимостью 1000 руб.
с годовой купонной ставкой 9%, имеющую рыночную цену 840
руб. Облигация будет приниматься к погашению через 8 лет.
Решение:
Слайд 18
Доходность облигаций
При сравнении доходности YTM облигаций (без
права досрочного погашения) с различной частотой начисления процентов —
годовое, квартальное, ежемесячное и т.д. — необходимо перейти от номинальной ставки (dn) к эффективной или сравнимой процентной ставке (de).
Эффективная ставка может быть рассчитана по формуле:
где dn -номинальная годовая процентная ставка (доходность);
de -эффективная годовая процентная ставка;
m -количество начислений процентов в год.
Слайд 19
Пример:
Необходимо определить эффективную среднегодовую процентную ставку при следующих
условиях - денежная сумма 1000 руб. приносит доход в
течение двух лет, годовая процентная ставка, по которой ежеквартально осуществляется начисление процента, составляет 10%.
Решение:
Слайд 20
Доходность облигаций
Оценка доходности на момент отзыва облигации с
рынка или ее досрочного погашения производится помощью показателя доходность
облигации с правом досрочного погашения (YTC).
Расчет YTC осуществляется на основе формулы оценки безотзывной облигации с постоянным доходом с выплатой процентов каждые полгода, в которой номинал заменен выкупной ценой Pm.
Слайд 21
Пример: Облигация номиналом 1000 руб. и погашением через

10 лет была выпущена 3 года назад. В настоящее
время ее цена равна 1050 руб. Проценты выплачиваются каждые полгода по ставке 14% годовых. В проспекте эмиссии указано, что в течение 5 лет предусмотрена защита от досрочного погашения. Выкупная цена превышает номинал на сумму годовых процентов. Рассчитать YTM, YTC.
Решение:
До погашения облигации осталось 7 лет, через 2 года облигация может быть досрочно погашена эмитентом (защита от досрочного погашения предусмотрена в течение 5 лет, с момента выпуска облигации прошло 3 года). Каждые полгода выплачивается купонный доход в размере 70 руб.
Доходность облигации без права досрочного погашения, или доходность к погашению (YTM), определяется с помощью функции Excel «Подбор параметра» на основе формулы оценки безотзывной облигации с постоянным доходом с выплатой процентов каждые полгода:
Доходность облигации с правом досрочного погашения (YTC) осуществляется с помощью функции Excel «Подбор параметра» на основе формулы оценки безотзывной облигации с постоянным дохо-дом с выплатой процентов каждые полгода, в которой номинал (N) заменен выкупной ценой (Pm = 1000 + 1000 * 0,14 = 1140 руб.):
Слайд 22
Доходность акций
Для оценки доходности бессрочной привилегированной акции используется
формула:
где D — ожидаемый дивиденд;
P0— текущая рыночная
цена акции.
Пример:
Компания «Иванов и Ко» эмитировала бессрочные привилегированные акции со ставкой 10%. Номинал акции — 100 руб., дивиденды выплачиваются поквартально. Акции продаются за 85 руб. Какова ожидаемая номинальная доходность акции? Какова ожидаемая эффективная годовая доходность?
Решение:
Слайд 23
Доходность акций
Доходность (ожидаемая) обыкновенной акции с равномерно возрастающим
дивидендом определяется по формуле:
где Di — ожидаемый дивиденд
(D i = D0 (1 + ), где D0 — последний полученный к моменту оценки дивиденд по акции );
P0— цена акции на момент оценки;
— темп прироста дивиденда.
Пример:
Согласно прогнозу, компания «Северные зори» выплатит очередной годовой дивиденд в размере 2 руб.; в дальнейшем дивиденды будут увеличиваться с темпом прироста 6% в год. Акции продаются по цене 22,22 руб. Какова ожидаемая доходность акции?
Решение:
Слайд 24
Оценка риска финансовых активов
При оценке риска финансовых
активов необходимо иметь в виду особенности применения статистических коэффициентов:
• Результативность операций с финансовыми активами принято измерять не доходом, а доходностью.
• Основными показателями оценки риска на рынке капиталов являются дисперсия и среднее квадратичное отклонение.
• На финансовом рынке большинство величин, представляющих интерес для инвесторов, оцениваются в вероятностных терминах.
Риск актива — величина непостоянная и зависит, в частности, от того, в каком контексте рассматривается данный актив: изолированно или как составная часть инвестиционного портфеля.
Слайд 25
Оценка риска финансовых активов
Оценка риска альтернативных вариантов
инвестиций в предположении, что каждый из них рассматривается изолированно
(общего риска) в вероятностных терминах, производится по следующему алгоритму:
1. Делаются прогнозные оценки значений доходности (di) и вероятностей их осуществления (pi);
2. Рассчитывается наиболее вероятная доходность (dml) по формуле:
3. Рассчитывается среднеквадратичное (стандартное) отклонение (σ) по формуле:
4. Рассчитывается коэффициент вариации:
Слайд 26
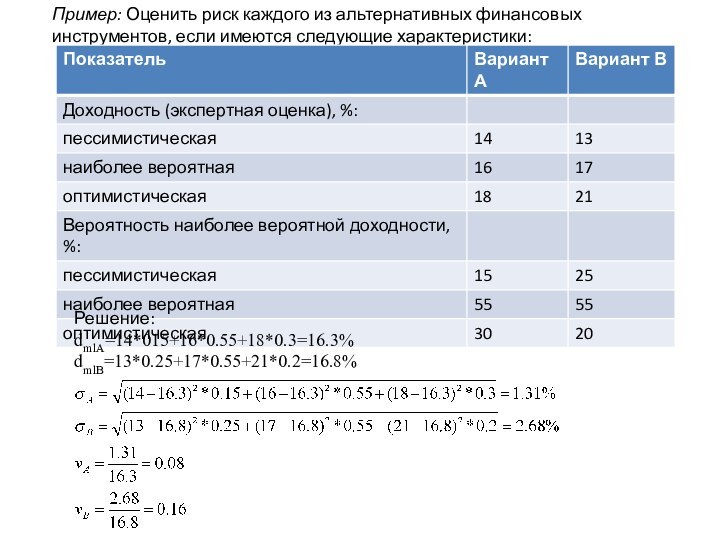
Пример: Оценить риск каждого из альтернативных финансовых инструментов,
если имеются следующие характеристики:
Решение:
dmlA=14*015+16*0.55+18*0.3=16.3%
dmlB=13*0.25+17*0.55+21*0.2=16.8%









































![Презентация по обучению грамоте на темуЗвук [о]. Буквы О, о](/img/tmb/7/630396/b1c3c62437009b2ed2d4748d98d53c05-210x.jpg)