Слайд 2
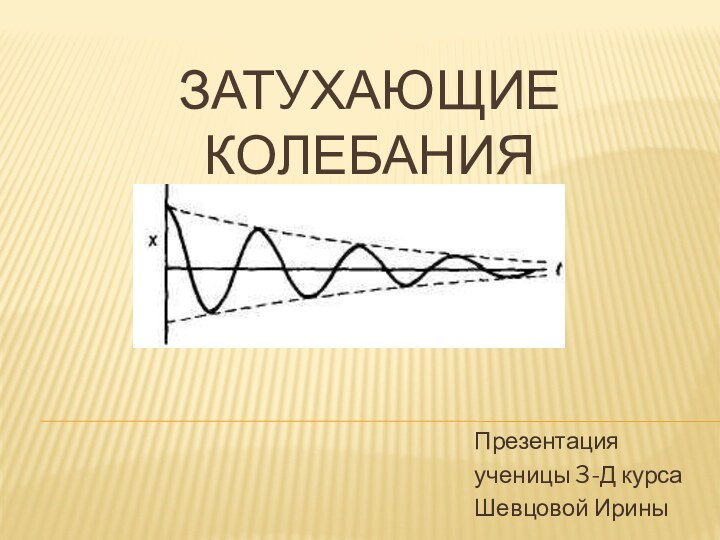
Свободные затухающие механические колебания
Затухающие колебания — колебания, энергия которых уменьшается
с течением времени. Все реальные колебания являются затухающими. Энергия механических
колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается.
Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например, маятник).
Слайд 3
Для колебаний под действием различных сил значения ,
, 0 будут различными. Например, для колебаний под действием
упругой силы
0 =k/m
= r/2m
= k/m - (r/2m)2
Слайд 4
Затухающие колебания представляют собой непериодические колебания, так как
в них не повторяется, например, максимальное значение амплитуды. Поэтому
называть - циклической (повторяющейся круговой) частотой можно лишь условно.
По этой же причине
= 2/ = 2/ 02 - 2 –
называется условным периодом затухающих колебаний.
Под условным периодом понимаем время между двумя прохождениями через положение равновесия в одном и том же направлении.
С увеличением трения «период» удлиняется.
Слайд 5
Автоколебания
При затухающих колебаниях энергия системы расходуется на преодоление
сопротивления среды. Если восполнять эту убыль энергии, колебания станут
незатухающими. Пополнение энергии системы может осуществляться за счет толчков извне, однако эти толчки должны сообщаться системе в такт с ее колебаниями, в противном случае они могут ослабить колебания и даже прекратить их совсем.
Можно сделать так, чтобы колеблющаяся система сама управляла внешним воздействием, обеспечивая согласованность сообщаемых ей толчков со своим движением.
Такая система называется
а в т о к о л е б а т е л ь н о й.
Слайд 6
Автоколебания
Характерная черта автоколебаний состоит в том, что их
амплитуда определяется свойствами самой системы, а не величиной начального
отклонения или толчка, как у свободных колебаний. Если, например, маятник часов отклонить слишком сильно, то потери на трение будут больше, чем поступление энергии от заводного механизма, и амплитуда будет уменьшаться. Наоборот, если уменьшить амплитуду, то избыток энергии, сообщаемой маятнику ходовым колесом, заставит амплитуду возрасти. Автоматически устанавливается такая амплитуда, при которой расход и поступление энергии сбалансированы.
Слайд 7
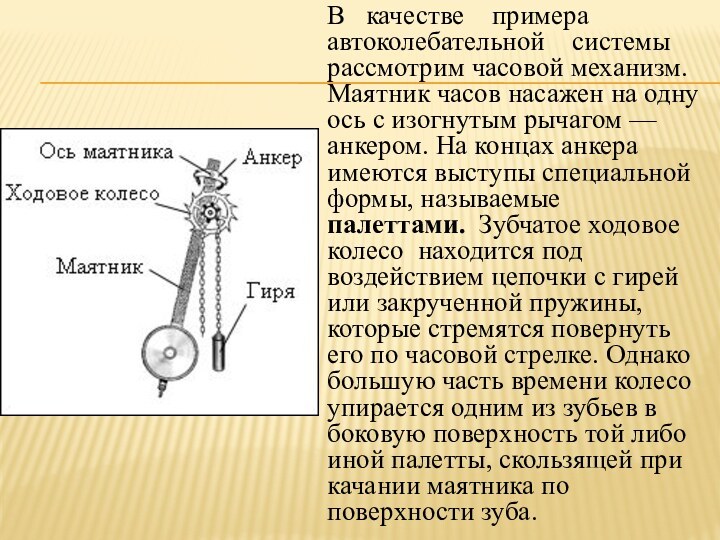
В качестве примера автоколебательной
системы рассмотрим часовой механизм. Маятник часов насажен на
одну ось с изогнутым рычагом — анкером. На концах анкера имеются выступы специальной формы, называемые палеттами. Зубчатое ходовое колесо находится под воздействием цепочки с гирей или закрученной пружины, которые стремятся повернуть его по часовой стрелке. Однако большую часть времени колесо упирается одним из зубьев в боковую поверхность той либо иной палетты, скользящей при качании маятника по поверхности зуба.
Слайд 8
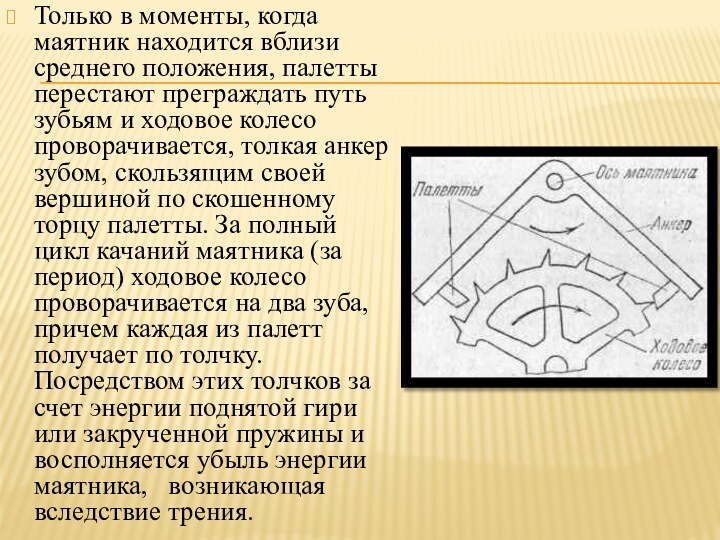
Только в моменты, когда маятник находится вблизи среднего
положения, палетты перестают преграждать путь зубьям и ходовое колесо
проворачивается, толкая анкер зубом, скользящим своей вершиной по скошенному торцу палетты. За полный цикл качаний маятника (за период) ходовое колесо проворачивается на два зуба, причем каждая из палетт получает по толчку. Посредством этих толчков за счет энергии поднятой гири или закрученной пружины и восполняется убыль энергии маятника, возникающая вследствие трения.
Слайд 9
Многие замечали, что обыкновенные качели можно раскачать без
всякого толчка извне. Для этого нужно, чтобы стоящие на
доске поочерёдно приседали и поднимались. Каждый партнёр приседает один раз за период колебаний качелей, а так как они делают это поочереди, то получается, что центр тяжести нашего маятника – качелей – дважды за период опускается и поднимается. Здесь показан способ возбуждения колебаний, принципиально отличающийся от рассмотренных ранее: колебательная система раскачивается со своей собственной частотой в результате того, что с удвоенной частотой меняется величина, от которой зависит период системы. Колебания возникают и поддерживаются за счёт работы, которая затрачивается на изменение периода системы.