график любой квадратичной функции, определять основные свойства функции по
графику.Цели:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
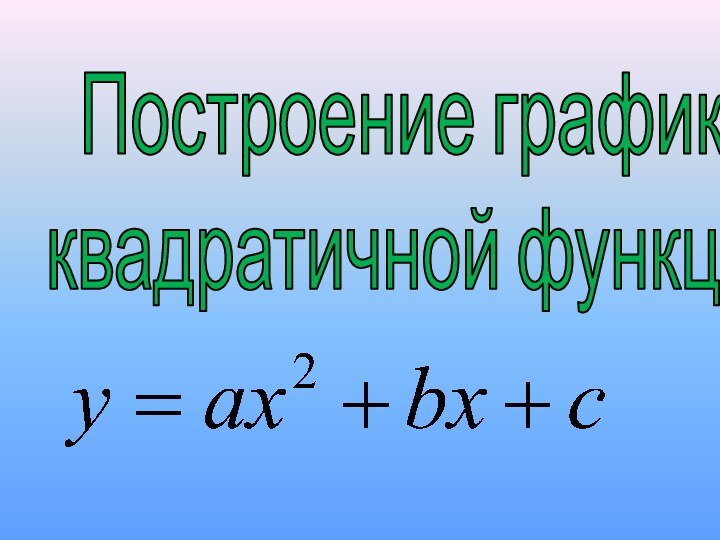






Цели:
. . . . . . .
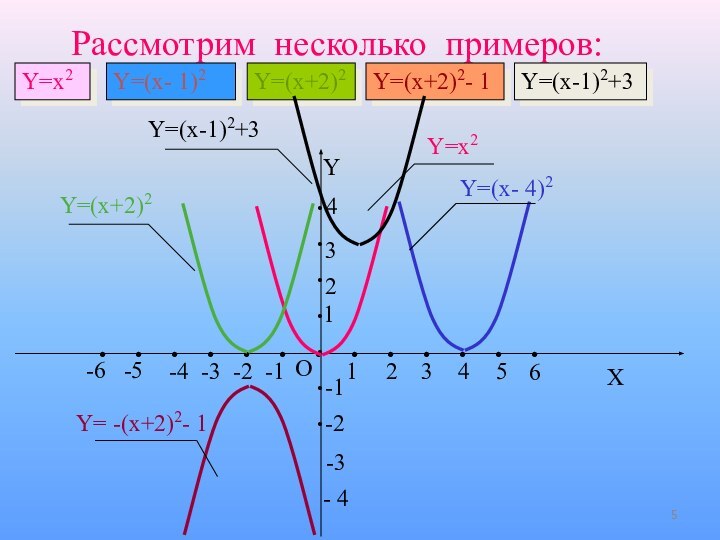
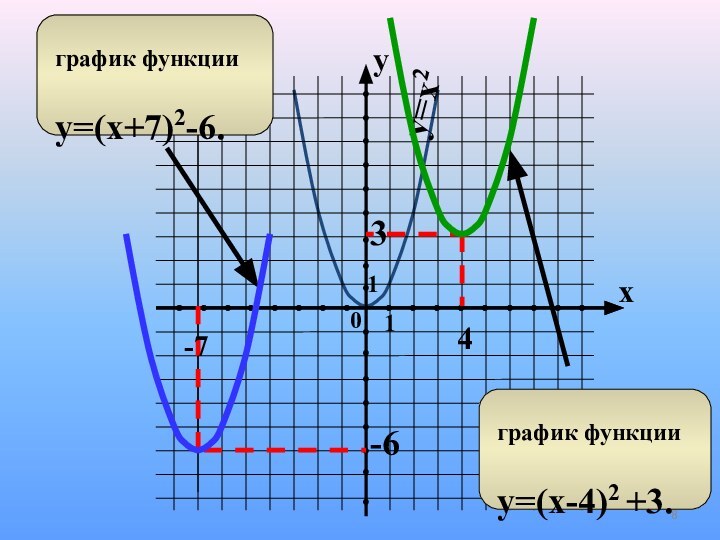
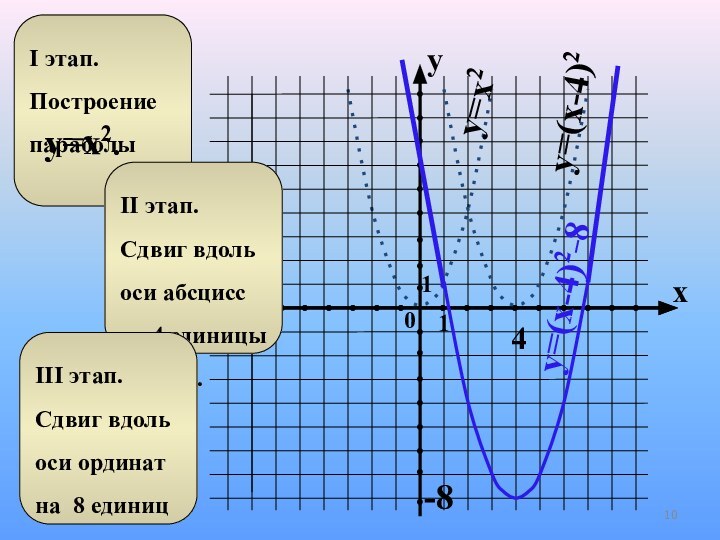
Y=x2
Y=(x- 4)2
Y=(x+2)2
Y= -(x+2)2- 1
Y=(x-1)2+3
1
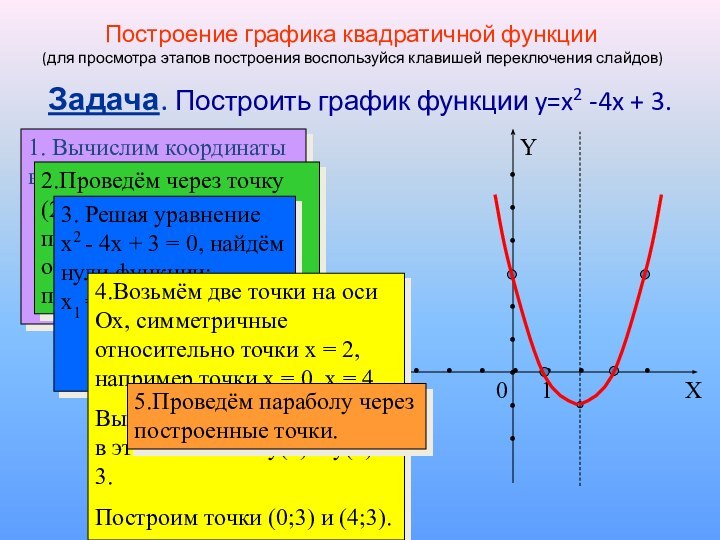
2.Проведём через точку (2;-1) прямую, параллельную оси ординат - ось симметрии параболы.
3. Решая уравнение x2 - 4x + 3 = 0, найдём нули функции: x1 = 1, x2 = 3.
Построим точки (1;0) и (3;0).
4.Возьмём две точки на оси Оx, симметричные относительно точки x = 2, например точки x = 0, x = 4.
Вычислим значение функции в этих точках: y(0) = y(4) = 3.
Построим точки (0;3) и (4;3).
5.Проведём параболу через построенные точки.
Построение графика квадратичной функции
(для просмотра этапов построения воспользуйся клавишей переключения слайдов)
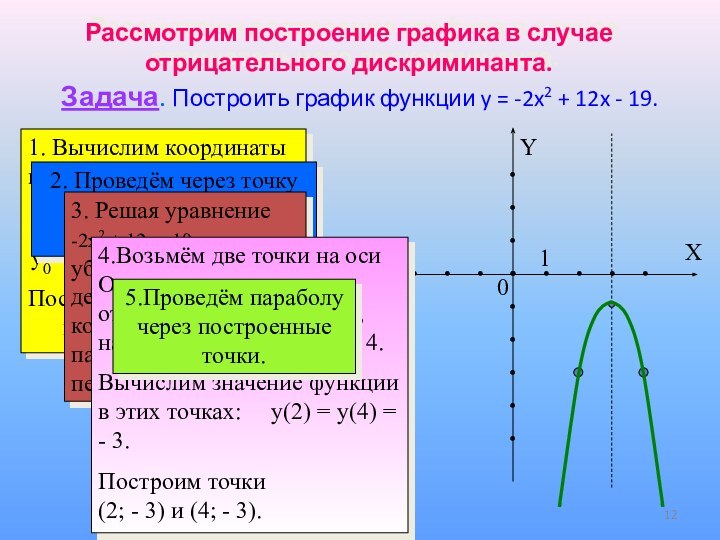
2. Проведём через точку (3;-1) ось симметрии параболы.
3. Решая уравнение -2x2 + 12x - 19, убеждаемся, что действительных корней нет, и поэтому парабола не пересекает ось Оx.
4.Возьмём две точки на оси Оx, симметричные относительно точки x = 3, например точки x = 2, x = 4.
Вычислим значение функции в этих точках: y(2) = y(4) = - 3.
Построим точки (2; - 3) и (4; - 3).
5.Проведём параболу через построенные точки.
ЗАПИШИ В ТЕТРАДЬ!