- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Применение производной в задачах ЕГЭ
Содержание
- 2. Наибольшее и наименьшее значения функцииРис.1Рис.2 Если производная положительна
- 3. Если функция непрерывна на отрезке, то
- 5. Задачи с решениями
- 6. Рис. 5Чертим эскиз графика функции (см. рис. 6).Рис.6
- 10. ПервообразнаяЗадача №5. На рис. 7 изображён график функции у=F(х), где F(х) – первообразная функции y=f(х).Рис. 7
- 11. 3.Площадь криволинейной трапеции и определенный интеграл
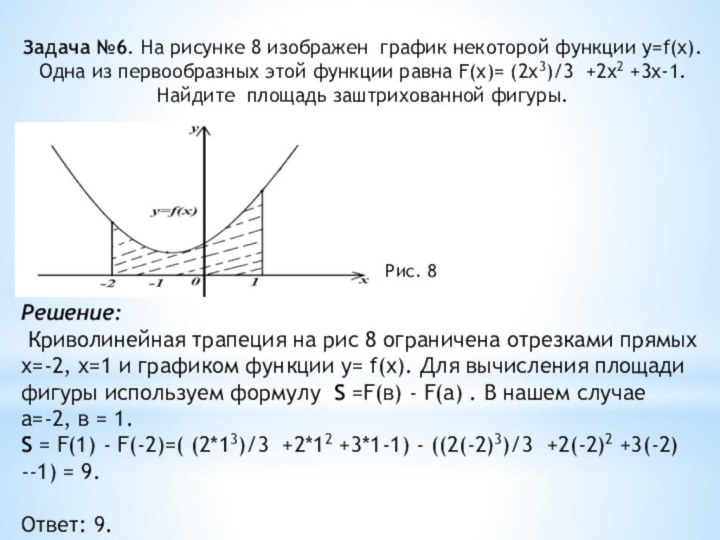
- 12. Задача №6. На рисунке 8 изображен график
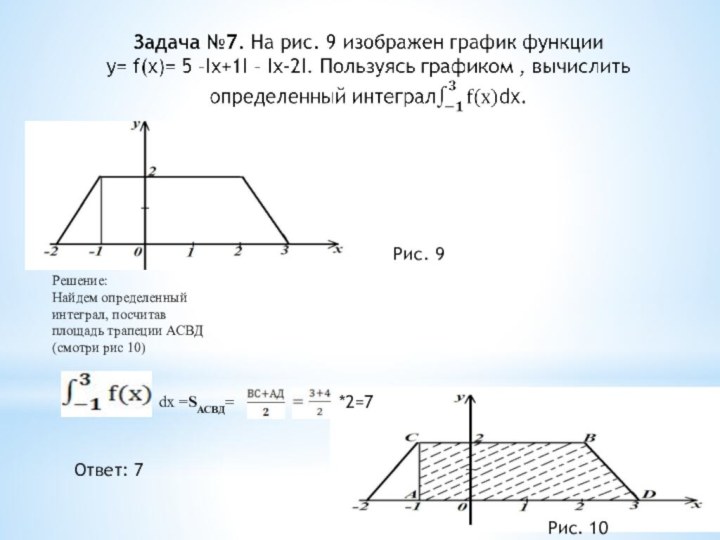
- 13. Рис. 9Рис. 10dх =SАСВД=Решение:Найдем определенный интеграл, посчитав площадь трапеции АСВД(смотри рис 10) *2=7Ответ: 7
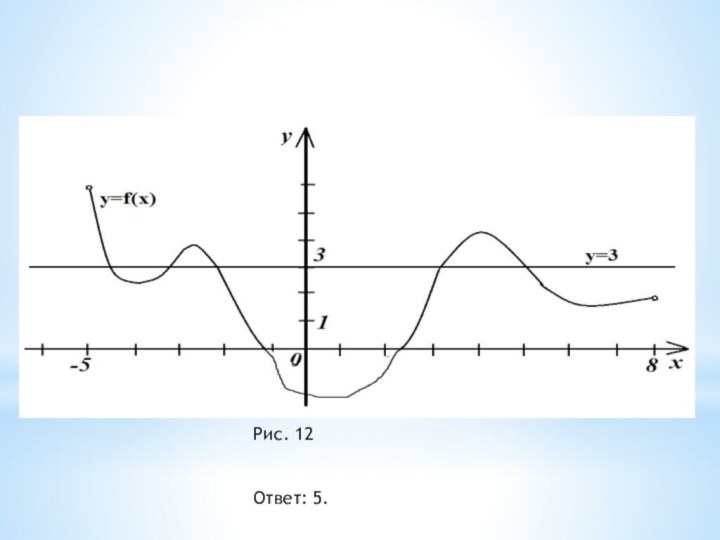
- 14. Задача №8. На рис. 11 изображен график
- 15. Скачать презентацию
- 16. Похожие презентации
Наибольшее и наименьшее значения функцииРис.1Рис.2 Если производная положительна (но при этом может быть равна нулю в некоторых точках отрезка), то функция возрастает на этом отрезке.












Слайд 3 Если функция непрерывна на отрезке, то она
принимает наибольшее и наименьшее значение либо на концах отрезка,
либо в тех точках, где производная равна нулю (или не существует). Поэтому один из способов отыскать наибольшее и наименьше значения функции на отрезке – посчитать ее значения на концах отрезка и в точках, где производная равна нулю (или не существует), и выбрать из них наибольшее или наименьшее значение.
Слайд 10
Первообразная
Задача №5. На рис. 7 изображён график функции
у=F(х), где F(х) – первообразная функции y=f(х).
Рис. 7
Слайд 12 Задача №6. На рисунке 8 изображен график некоторой
функции y=f(х). Одна из первообразных этой функции равна F(х)=
(2х3)/3 +2х2 +3х-1. Найдите площадь заштрихованной фигуры.Рис. 8
Решение:
Криволинейная трапеция на рис 8 ограничена отрезками прямых х=-2, х=1 и графиком функции у= f(х). Для вычисления площади фигуры используем формулу S =F(в) - F(а) . В нашем случае
а=-2, в = 1.
S = F(1) - F(-2)=( (2*13)/3 +2*12 +3*1-1) - ((2(-2)3)/3 +2(-2)2 +3(-2) --1) = 9.
Ответ: 9.
Слайд 13
Рис. 9
Рис. 10
dх =SАСВД=
Решение:
Найдем определенный интеграл, посчитав площадь
трапеции АСВД(смотри рис 10)
*2=7
Ответ: 7
Слайд 14 Задача №8. На рис. 11 изображен график функции
y=f(х)., определенной на интервале(-5; 8). Найдите количество точек в
которых касательная к графику функции F(х),которая является первообразной для функции f(х), параллельна прямой у=3х+8 или совпадает с ней.Рис. 11