Презентация на тему Практикум решения олимпиадных задач по теме Некоторые приёмы решения целых уравнений

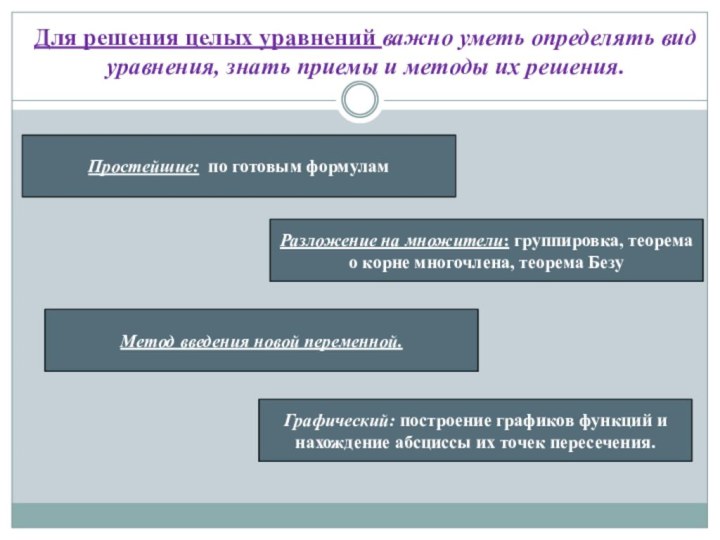
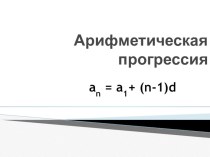
степени имеет не более n корней (с учетом их

кратностей). Например, многочлен третьей степени не может иметь четыре корня.
2. Многочлен нечетной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т. д. степени имеют хотя бы один корень. Многочлены четной степени корней могут и не иметь.
3. Если на концах отрезка [а; b] значения многочлена имеют разные знаки
(т. е. Рn(а) · Рn(b) < 0), то на интервале (а; b) находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.
4. Если число с является корнем многочлена Рn(х), то этот многочлен можно представить в виде произведения Рn(х) = (х - с)Рn-1(х), где Рn-1(x) - многочлен (n - 1)-й степени. Другими словами, многочлен Рn(х) можно разделить без остатка на двучлен (х - с). Это позволяет уравнение n-й степени сводить к уравнению (n - 1)-й степени (понижать степень уравнения).
5. Если многочлен со всеми целыми коэффициентами (причем свободный член а0 ≠ 0) имеет целый корень с, то этот корень является делителем свободного члена а0. Такое утверждение позволяет подобрать целый корень многочлена (если он есть).

уравнения, знать приемы и методы их решения.
Простейшие: по готовым

формулам

Разложение на множители: группировка, теорема о корне многочлена, теорема Безу

Метод введения новой переменной.

Графический: построение графиков функций и нахождение абсциссы их точек пересечения.

квадратным
5х2=9х2-4х2
х4+6х3+9х2-4х2-12х+3=0
(х4+6х3+9х2)-(4х2+12х)+3=0
(х2+3х)2-4(х2+3х)+3=0
Пусть t=х2+3х, тогда
t2-4t+3=0


х2+3х=3

х2+3х=1

х2+3х-3=0 х2+3х-1=0

Ответ:

х4+4х3-8х+4=0

Дополнительное задание:

Решим уравнение: х4+6х3+5х2-12х+3=0

- 2 = 0.
Решение:
Если это уравнение имеет целый корень,

он является делителем свободного члена (-2), т. е. равняется одному из чисел: ±1, ±2. Проверка показывает, что корнем уравнения является число 2. Тогда многочлен Р3(х) = х3 - 7х2 + 11х - 2 можно представить в виде произведения Р3(х) = (х - 2)P2(х), т. е. многочлен Р3(х) можно без остатка разделить на двучлен (х - 2). Выполним такое деление «уголком».
Напомним, что деление «уголком» осуществлялось таким образом, чтобы на каждом промежуточном этапе деления исчезала старшая степень промежуточного делимого.
Таким образом, мы разложили левую часть уравнения на множители:
(х - 2)(х2 - 5х + 1) = 0 .
х - 2 = 0  x1 = 2. х2 - 5х + 1 = 0 дает еще два корня 

Ответ: 2,

Дополнительное задание: х3 + 5х2 - 4х - 2 = 0,
х3 – x2 – 3x – 1 = 0

уравнения является по парное равенство коэффициентов относительно среднего члена

уравнения(коэффициент при х4 и свободный член равны 1; коэффициент при х3 и х равны -7 и -7 соответственно)

Для решения уравнения такого типа существует следующий приём. Прежде всего убедится, что х=0, не является корнем уравнения. Разделим все члены уравнения на х2.

=0, сгруппируем

Пусть

,тогда

у2-7у+6=0, у1=6; у2=1

-х+1=0

не имеет корней

х2-6х+1=0

Решение:

х4-2х3-х2-2х+1=0

Дополнительные задания:

х4+2х3-5х2-2х+1=0

2х4+3х3-16х2+3х+2=0

2х4+х3-6х2+х+2=0

2х4+3х3-4х2-3х+2=0

Х4-7х3+14х2-7х+1=0

Учитывая закономерности в коэффициентах этого уравнения, подобные уравнения называют возвратными, или симметричными.

бы один корень(делитель свободного члена 1:+1,-1). Проверка показывает, что

корнем является Х=-1. Поделим «углом» на (х+1)

(х+1)(х6+х5-6х4-7х3-6х2+х+1)=0

Пусть

х=-1, х6+х5-6х4-7х3-6х2+х+1=0-симметричное уравнение чётной степени, поделим на х3

Имеем

Сгруппируем:

,тогда

Не имеет корней

Ответ:

-1

Решение

для а>0, неравенство выполняется при а=1
Имеем х=1
Ответ:1

- 3х + 1 = 0.
Решение:
Проверка показывает, что данное

уравнение с целыми коэффициентами не имеет целых корней ±1 (делители свободного члена). Поэтому уравнение вообще не имеет целых корней. Предположим, что корни являются рациональными числами.
Введем новую переменную у = 1/x, откуда х = 1/y. Тогда уравнение имеет вид:    или у3 - 3у2 - 10у + 24 = 0. Попробуем подобрать корень этого уравнения среди делителей числа 24 (свободный член). Проверка показывает, что у = 2 - корень этого уравнения. Далее понижаем степень этого уравнения:

Корнями квадратного уравнения у2 - у - 12 = 0 являются числа у = -3 и у = 4. Вернемся теперь к старой неизвестной
х = 1/y и найдем три корня данного уравнения: 

1 = 0.
Решение:
х4 – x3 – 12x2 + 7х - 1 =(х2

+ ах + 1)(х2 + bx- 1)=х4 + bх3 – х2 + ах3 + abx2 - ах + х2 + bх - 1 = х4 + (а + b)х3 + abx2 + (b - a)x -1,
х4 – x3 – 12x2 + 7х - 1 = х4 + (а + b)х3 + abx2 + (b - a)x -1.
Приравняем коэффициенты при одинаковых степенях х данного и полученного многочленов. Имеем систему уравнений


Из первого и третьего уравнений системы найдем а = -4 и b = 3. Проверим, что эти значения удовлетворяют и второму уравнению.
  Тогда данное уравнение будет иметь вид: (х2 - 4х + 1)(х2 + 3х -1) = 0.
Уравнение х2- 4х + 1 = 0 имеет корни 
 
уравнение х2 + 3х - 1 = 0 – корни

Дополнительное задание. 1) х4 + x3 – 6x2 - 5х + 3 = 0.
2) При каких числах а и в многочлен ах4 + вx3  + 17x2 - 12х + 20 делится без остатка на многочлен (х – 2).2 

если функция у= f (х) убывает, а функция у=g(х)

возрастает и если уравнение
f (х)=g(х) имеет корень, то только один.

x5+2x-3 = 0,
x5 =-2x+3.
 
y=x5 - возрастающая, а
у=-2х+3- убывающая,
то корень у заданного уравнения один, и этим корнем является значение х=1. Это хорошо видно из приведенного рисунка.
Ответ: х = 1.

Решим уравнение х5+ 2х - 3 = 0.

в)(х +с)(х+к)= р сводится к квадратному, если
а +с=

в + к или а + в = с +к и т. д.

1+5=2+4, мы видим симметрию левой части.
(х2 +6х+5) (х2 + 6х+8) = 40,
х2 +6х+5 = t,
t (t+3)= 40, t2 +3t -40=0
t =-8 или t=5.

Получаем х2 +6х+5= 5, где х=0 , х=-6
х2 +6х+5 = -8, не имеет корней
Ответ: -6,0.

Дополнительное задание: (х+2)(х-3)(х+1)(х+6)=-96,
(х-1)(х-3)(х+5)(х+7)=-297,
(х+1)(х+3)(х+5)(х+7) -15=0

видим симметрию левой части
Произведение 1 и 4, 2 и

3 множителей заменим квадратными трехчленами
(х2 + 14х + 24)(х2 + 11х +24)= 4х2 .

Обе части уравнения разделим на х2 ≠ 0 и получим уравнение
(х+24/х +14)(х+24/х +11)=4.

Пусть х+24/х = у, тогда (у+14)(у+11)=4,
Получим квадратное уравнение у2 +25у+150=0, у1 = — 10 и у2 = — 15.

х+24/х=-10 х+24/х=-15
х2+10х+24=0 х2+15х+24=0
х1=- 4, х2= -6

Дополнительное задание: (х+4)(х-2)(х+5)(х-10)+54х2 =0

+ в)4=с, решается заменой х = t -(a+b):2.
Введем замену

х = t -(6+4):2=t-5. Тогда уравнение имеет следующий вид:
(t-5+6)4+(t-5+4)4=82,
((t2+1)2)2+(( t-1)2)2=82,
(t2+2 t +1)2+(t2-2 t +1)2=82,
2t4+12t2-80=0,
t4+6t2-40=0, пусть t2=m, m≥0,
m2+6 m-40=0,
m1=4, m2=-10- не удовлетворяет условию,
t2=4, t=+2,-2,
х1=-3,х2=-7.
Ответ:-3,-7.

Дополнительное задание: (х+2)4+х4=82.

- 2а2х = 0.
Решение:
Отметим, что в это уравнение переменная

х входит в третьей степени (и ниже), переменная а - во второй степени (и ниже). Поэтому удобно рассматривать такое уравнение как квадратное по переменной а.

Запишем его в виде 2хa2 + (х2 + 2)a - (х3 - 2х) = 0.
Найдем  D = (x2 + 2)2 + 8х(х3 - 2х) = (3х2 - 2)2 и корни и a = -x.
Вернемся к старой неизвестной х.
Уравнение   или х2 - 2ах – 2=0, имеет корни 

Уравнение а = -х имеет корень х3 = -а.

Ответ: х3 = -а.