- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Показательная функция, ее свойства и применение.Показательная функция, ее свойства и применение.
Содержание
- 2. Основная цель: Актуализация базовых знаний и способов действий по теме.
- 3. Показательная функция, ее свойства и применение. Степень
- 4. Свойства степени с рациональным показателемЕсли а>0, то:1.2..3.4.5.6.
- 5. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯСВОЙСТВА И ГРАФИК«Деятельность учителя неотделима от
- 6. ОпределениеФункция, заданная формулой у=аx (где а>0, a≠1), называется показательной функцией с основанием а х х
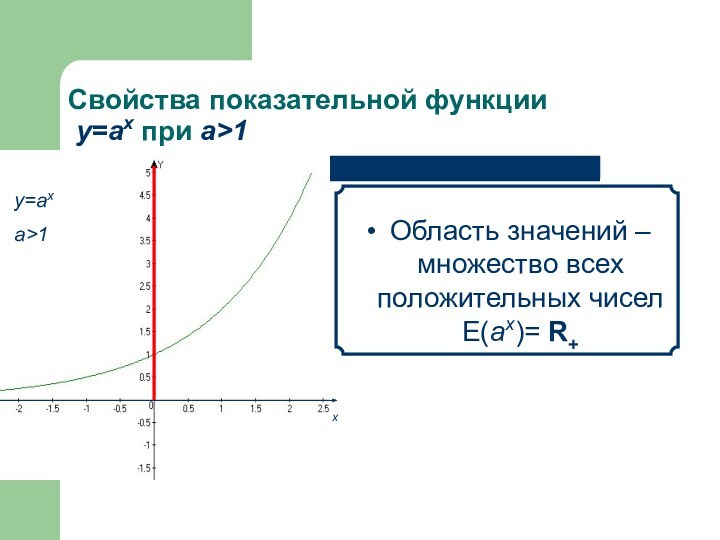
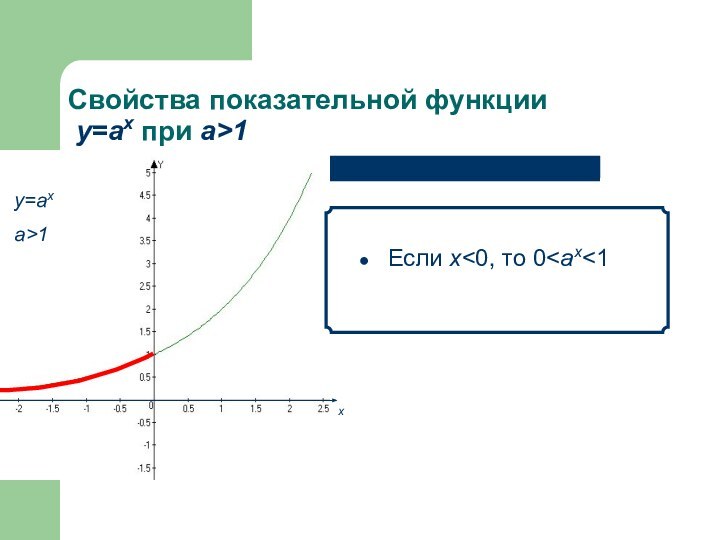
- 7. Свойства показательной функции у=аx при а>1
- 8. Свойства показательной функции у=аx при а>1
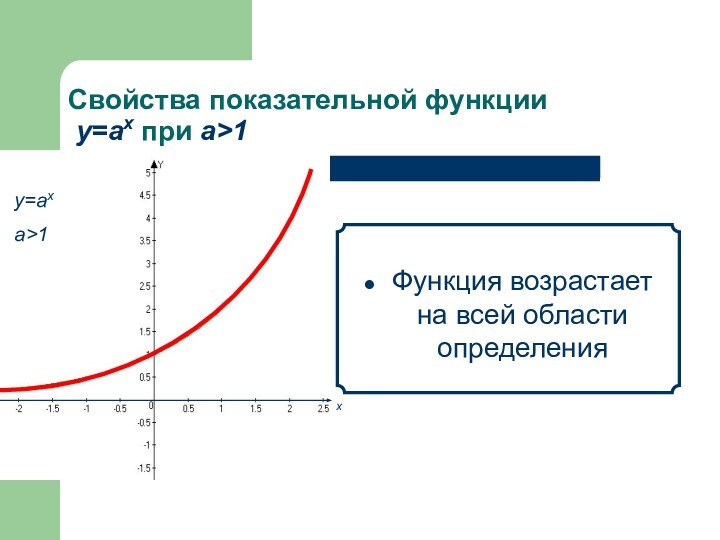
- 9. Свойства показательной функции у=аx при а>1 Функция возрастает на всей области определения х
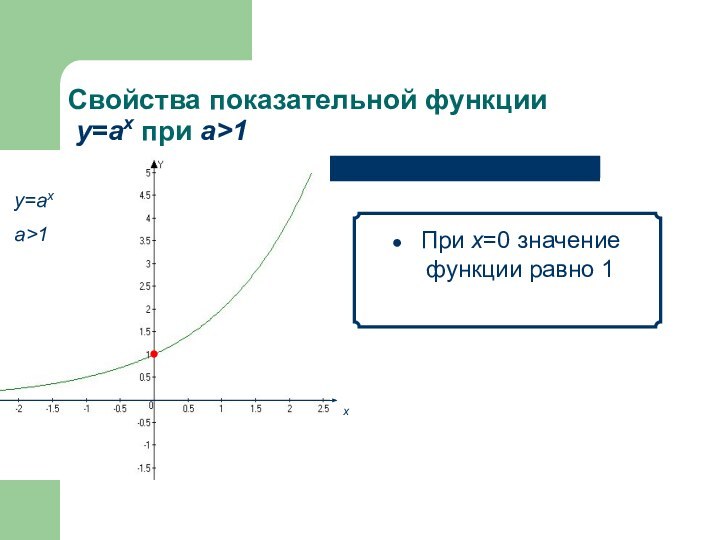
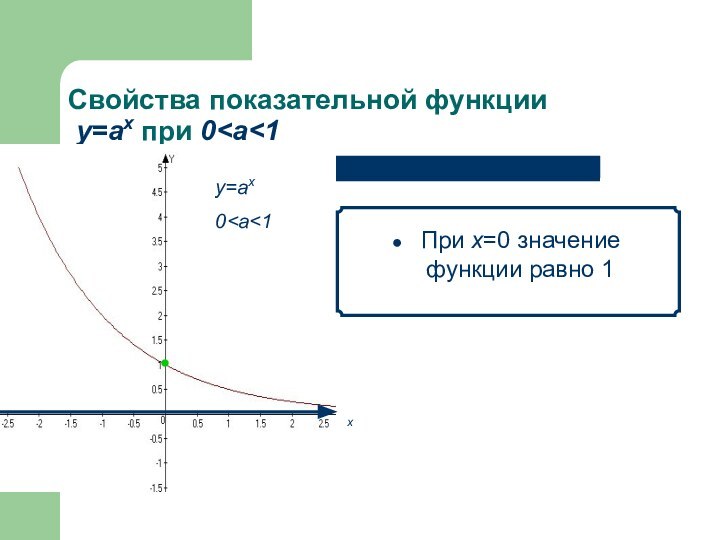
- 10. Свойства показательной функции у=аx при а>1 При х=0 значение функции равно 1 х
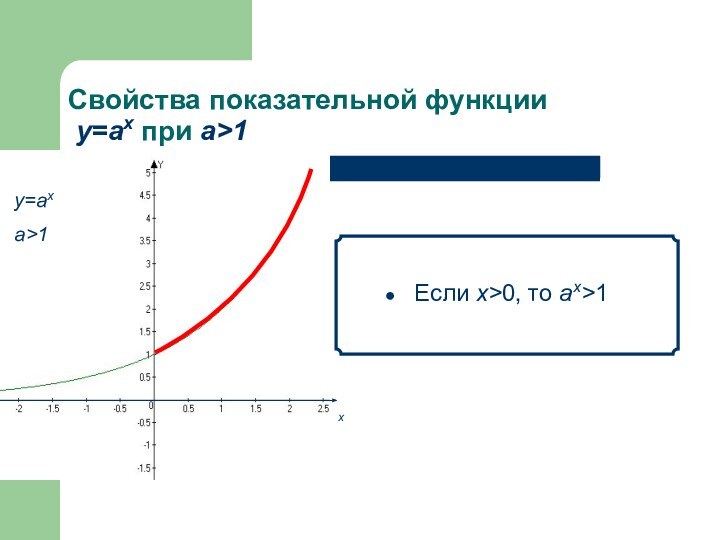
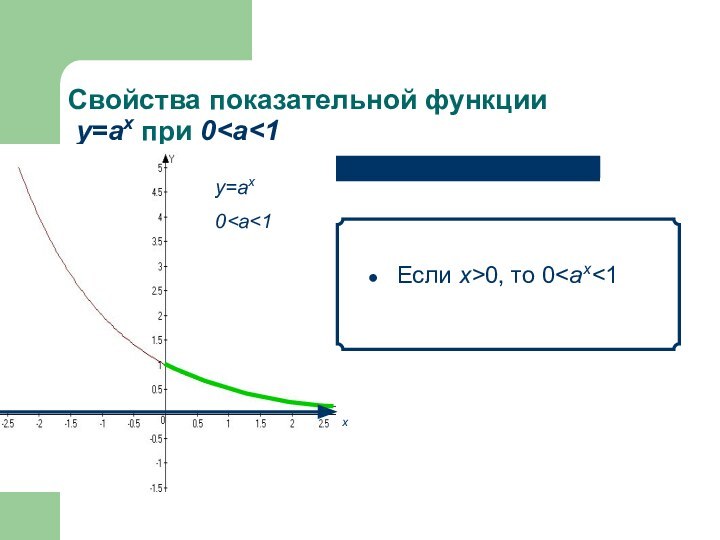
- 11. Свойства показательной функции у=аx при а>1 Если х>0, то аx>1 х
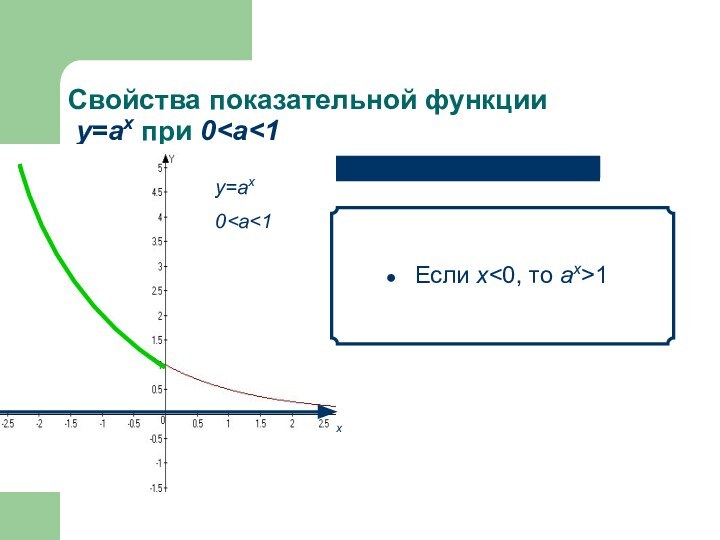
- 12. Свойства показательной функции у=аx при а>1 Если х
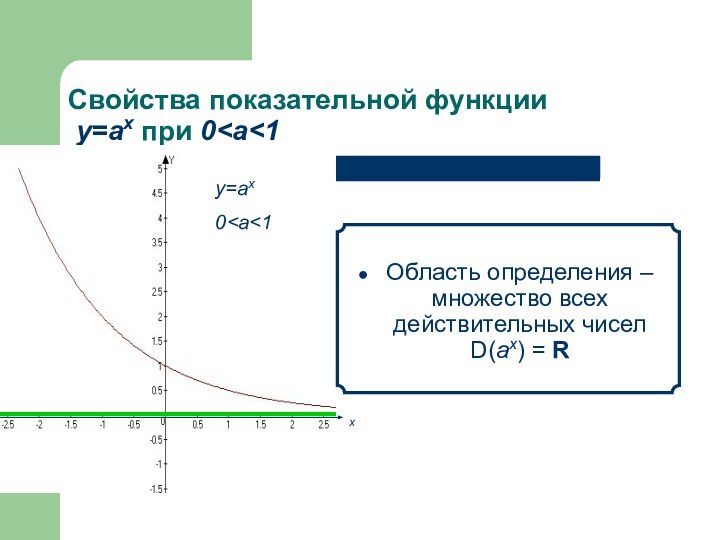
- 13. Свойства показательной функции у=аx при 0
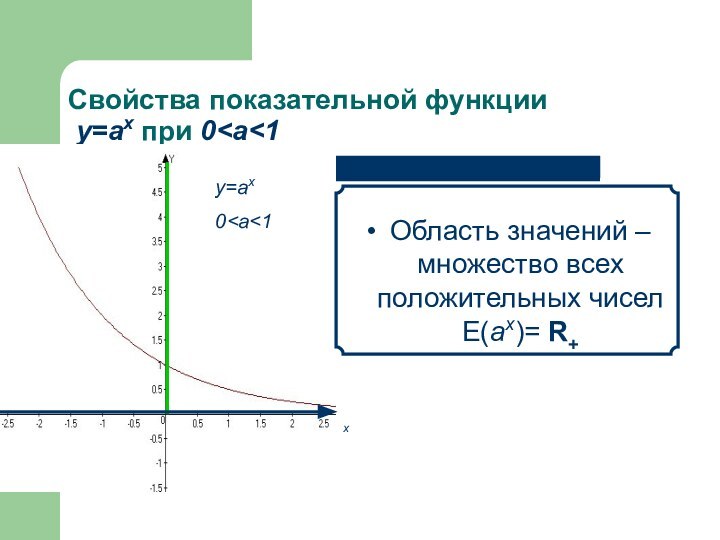
- 14. Свойства показательной функции у=аx при 0
- 15. Свойства показательной функции у=аx при 0
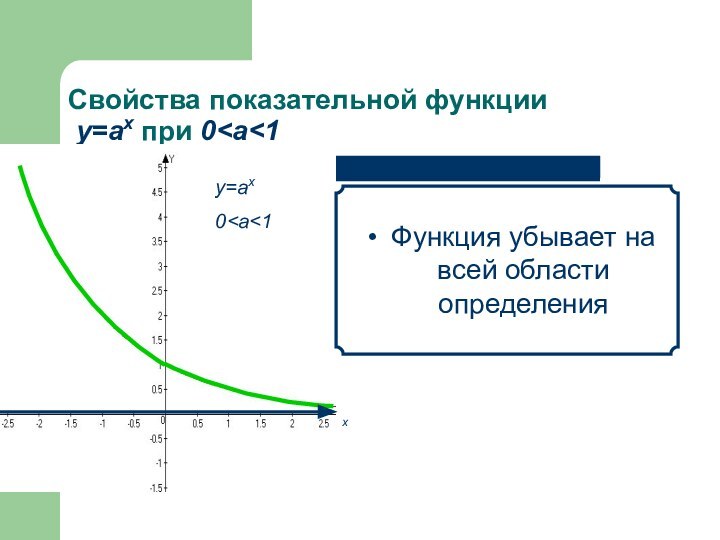
- 16. Свойства показательной функции у=аx при 0
- 17. Свойства показательной функции у=аx при 0
- 18. Свойства показательной функции у=аx при 0
- 19. Показательные уравнения
- 20. Показательные неравенства ЕслиЕслине имеет решения
- 21. Производная и первообразная
- 22. Тест 1Проверь себя!Да.
- 23. Тест 2 Проверь себя !«-» 8. «-»
- 24. Основные опорные сигналы1.
- 25. Способы решения уравненийРазложение левой части на множители.Замена
- 26. Проверь себя! Тест 3, часть 11.
- 27. Указания к заданиям 16 - 1916. Используйте
- 28. Решите. Тест 3 (часть2)Вариант 1.Решите уравнение, в
- 29. Проверь себя!Вариант 1 Решите уравнение. В
- 30. Проверь себя!Вариант 2Решите уравнение.Решение. Так как при любых х, то Ответ: -2
- 31. Скачать презентацию
- 32. Похожие презентации
Основная цель: Актуализация базовых знаний и способов действий по теме.




















Слайд 3
Показательная функция, ее свойства и применение.
Степень с
рациональным показателем.
Показательная функция.
Показательные уравнения.
Показательные неравенства.
Дополнительный справочный материал.
Слайд 4
Свойства степени с рациональным показателем
Если а>0, то:
1.
2.
.
3.
4.
5.
6.
7.
8.
10.
11.
Если
при r>0 и
при r<0;12. Если
то
При a>1 и
при 0 9.
Слайд 5
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
СВОЙСТВА И ГРАФИК
«Деятельность учителя неотделима от деятельности
учащихся… Она должна состоять из трех основных этапов: мотивационного,
операционно-познавательного и рефлексивно-оценочного».Фридман Л.М.
Слайд 6
Определение
Функция, заданная формулой у=аx (где а>0, a≠1), называется
показательной функцией с основанием а
х
х
Слайд 7
Свойства показательной функции
у=аx при а>1
Область определения
– множество всех действительных чисел D(аx) = R
х
Слайд 8
Свойства показательной функции
у=аx при а>1
Область значений
– множество всех положительных чисел E(аx)= R+
х
Слайд 9
Свойства показательной функции
у=аx при а>1
Функция возрастает
на всей области определения
х
Слайд 13 Свойства показательной функции у=аx при 0
– множество всех действительных чисел D(аx) = R
х
Слайд 22
Тест 1
Проверь себя!
Да.
11. Да.
Нет. 12. Да.
Нет. 13. Да.
Да. 14. Нет.
Да. 15. Да.
Да. 16. Да.
Да. 17. Да.
Нет. 18. Да.
Нет. 19. Нет.
Нет. 20. Да.
Слайд 23
Тест 2
Проверь себя !
«-» 8. «-»
15. «+»
«-»
9. «+» 16. «-»«+» 10. «-» 17. «+»
«-» 11. «+» 18. «-»
«+» 12. «+» 19. «-»
«-» 13. «+» 20. «-»
«+» 14. «+» 21. «+»
18-21 правильных ответов – «5», 14-17 – «4», 11-13 – «3»,
меньше 11 – не владеете материалом
Слайд 25
Способы решения уравнений
Разложение левой части на множители.
Замена переменной.
Функциональный
(с помощью свойств функции).
Однородные (делением обеих частей на выражение
не равное нулю)Графический.
Логарифмирование.
Слайд 26
Проверь себя! Тест 3,
часть 1
1. Опора 9
, функциональный способ
2. Опора 1 , функциональный способ
3. Опора 8 , замена переменной, функциональный способ
4. Опора 3 , функциональный способ, метод интервалов
5. Опора 6 , однородные уравнения
6. Опора 2 , замена переменной, разложение на множители
7. - замена переменной, метод интервалов
8. Опора 7 , функциональный способ
9. Опора 2 , замена переменной, функциональный способ
10. Опора 5 ,
11. Опора 1 , функциональный способ
12. - , графический способ
13. Опора 5 , геометрическая прогрессия
14. Опора 4 , функциональный способ
15. - , замена переменной, метод интервалов
Слайд 27
Указания к заданиям 16 - 19
16. Используйте основное
свойство дроби и исследование решений линейного уравнения.
17.
18. Базовые
знания – производная и первообразная показательной функции.19. Записать данную функцию в виде степени с основанием 2. опереться на свойства показательной и квадратичной функций.
Слайд 28
Решите. Тест 3 (часть2)
Вариант 1.
Решите уравнение, в ответ
запишите наименьший корень
Вариант 2.
Решите уравнение, в ответ запишите корень
или сумму корней Вариант 3.
Решите уравнение
Слайд 29
Проверь себя!
Вариант 1
Решите уравнение. В ответ
запишите наименьший корень
Решение.
Ответ: -





























