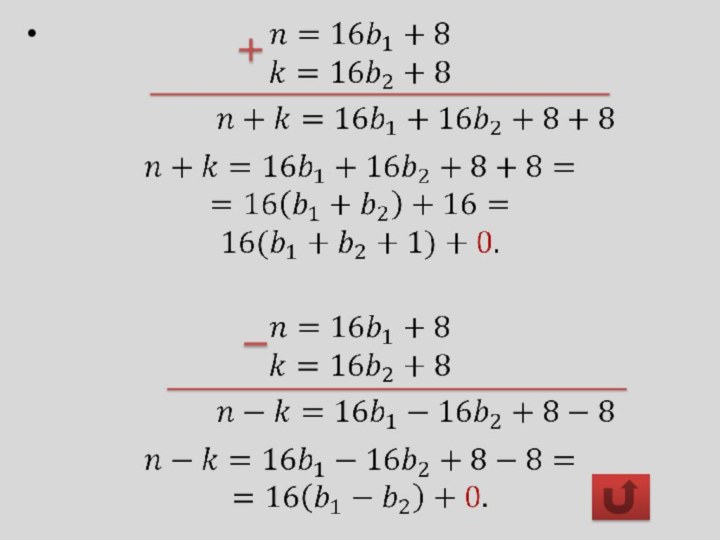Презентация на тему Натуральные и целые числа. Делимость целых чисел. НОД и НОК натуральных чисел

это числа, которые используются для счета.
3+33=36
12*3=36
Не всегда выполняется «-»

и «:»
14-15=-1
9:2=4,5

Обозначение: N

это все натуральные числа, «0» и противоположные натуральным.
3+33=36
12*3=36
14-15=-1

Не всегда выполняется «-» и «:»
9:2=4,5

Обозначение: Z

b. Если существует такое q, что выполняется равенство
a=

bq,
то говорят, что число a делится на число b.
a – делимое, b – делитель, q – кратное

Сравните:
a:b

на число 2, если его последняя цифра четная или

0;
Число делится на число 3, если сумма его цифр делится на 3;
Число делится на число 4, если две его последние цифры образуют число, которое делится на 4, или являются нулями.

последняя цифра 0 или 5;
5. Число делится на число

8, если три его последние цифры образуют число, которое делится на 8, или являются нулями;
6. Число делится на число 9, если сумма его цифр делится на 9;
7. Число делится на число 10, если его последняя цифра нуль.

что каждая из трех его средних цифр на 1

больше предыдущей.

Пусть - искомое число.

1) b=a+1
c=a+2
d=a+3

2) Так как , то
e={0,5}

e=0 , то a+(a+1)+(a+2)+(a+3)+0=4a+6,

(4a+6)/9

Тогда a=3
a=6
a=9 - не подходит

Если a=3, то 4а+6=18, 18/9 - подходит

Если a=6, то 4а+6=30, не подходит

34560

Если a=3, то 4а+6=18, 18/9 - подходит

, то

a=1, 4+11=15
a=2, `8+11=19
a=3, 12+11=23
a=4, 16+11=27
a=5, 20+11=31
a=6, 24+11=35

45675

Ответ: 34560 и 45675

только два делителя – само себя и 1, то

его называют простым числом; если оно имеет более двух делителей, то его называют составным числом.
Число 1 не является ни простым, ни составным.

b и а не делится на b, то существует,

и притом только одна, пара натуральных чисел q и r, причем r < b, такая, что выполняется равенство
a = bq+r.

4, 5, 6, 8, 9, 10, 15, 18, 20

делится без остатка число
562 320.
№ 2
Определите, простым или составным является число 87 516 540 321.
№ 3
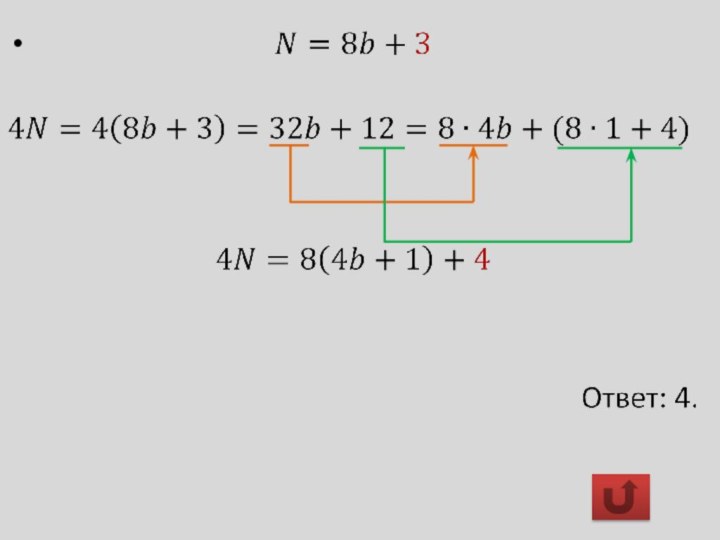
Число N дает при делении на 8 остаток 3. Какой остаток при делении на 8 дает число в четыре раза больше данного?

остаток 8. Доказать, что разность и сумма этих чисел

без остатка делятся на 16.

№ 5
Разложить на простые множители число 7000.

чисел а, Ь, с, ... называется наибольшее натуральное число, на которое

делятся нацело числа а, Ь, с, …

Теорема. Если даны два натуральных числа a и p, причем p – простое число, то либо a делится на p, либо a и p – взаимно простые числа.

разложения на простые множители чисел  а, Ь, с, ...;
2) перечисляют

все простые множители, входящие во все разложения;
3) каждый из перечисленных множителей возводят в минимальную степень, с которой этот множитель входит в разложения.

72.
Решение:

 
 

разложения на простые множители чисел а, Ь, с,...;
2) перечисляют

все простые множители, входящие хотя бы в одно из этих разложений;
3) каждый из перечисленных множителей возводят в максимальную степень, с которой этот множитель входит в разложения;
4) произведение полученных степеней простых множителей дает НОК чисел а, Ь, с, …

2;
5 + 6 + 2 + 3 + 2

+ 0 = 18, 18 делится на 3 и на 9, значит 562320 делится на 3 и на 9;
562320 – две последние цифры образуют число 20, которое делится на 4, значит 562 320 делится на 4;
562320 – оканчивается на 0, значит 562320 делится на 5 и на 10;
Т.к. 562320 делится на 2 и на 3, а числа 2 и 3 – взаимно простые, то 562320 делится на произведение 2 и 3, т.е. на 6;
562320 – три последние цифры образуют число 320, которое делится на 8, значит 562320 делится на 8;
Т.к. 562320 делится на 3 и 5 (3 и 5 – взаимно простые), то 562320 делится на 15;
Т.к. 562320 делится на 2 и 9 (2 и 9 – взаимно простые), то 562320 делится на 18;
Т.к. 562320 делится на 4 и 5 (4 и 5 – взаимно простые), то 562320 делится на 20.

516 540 321, отличный от 1 и самого этого

числа, то 87 516 540 321 – составное.
8 + 7 + 5 + 1 + 6 + 5 + 4 + 0 + 3 + 2 + 1 = 42
42 делится на 3, значит и число
87 516 540 321 делится на 3, а значит заданное число является составным.