- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Теория вероятности
Содержание
- 2. На экзамен вынесено 60 вопросов, Андрей не
- 3. На экзамен вынесено 60 вопросов, Андрей не
- 4. В фирме такси в данный момент свободно
- 5. В фирме такси в данный момент свободно
- 6. В случайном эксперименте бросают две игральные кости.
- 7. В случайном эксперименте бросают две игральные кости.
- 8. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
- 9. В случайном эксперименте симметричную монету бросают дважды.
- 10. При производстве в среднем на каждые 2982
- 11. При производстве в среднем на каждые 2982
- 12. Научная конференция проводится в 5 дней. Всего
- 13. Научная конференция проводится в 5 дней. Всего
- 14. Вася, Петя, Коля и Лёша бросили жребий
- 15. Вася, Петя, Коля и Лёша бросили жребий
- 16. Перед началом футбольного матча судья бросает монетку,
- 17. Перед началом футбольного матча судья бросает монетку,
- 18. Если шахматист А. играет белыми фигурами, то
- 19. Если шахматист А. играет белыми фигурами, то
- 20. Вероятность того, что батарейка бракованная, равна 0,06.
- 21. Вероятность того, что батарейка бракованная, равна 0,06.
- 22. Вероятность того, что новый электрический чайник прослужит
- 23. Вероятность того, что новый электрический чайник прослужит
- 24. Из районного центра в деревню ежедневно ходит
- 25. Из районного центра в деревню ежедневно ходит
- 26. Помещение освещается фонарём с двумя лампами. Вероятность
- 27. Помещение освещается фонарём с двумя лампами. Вероятность
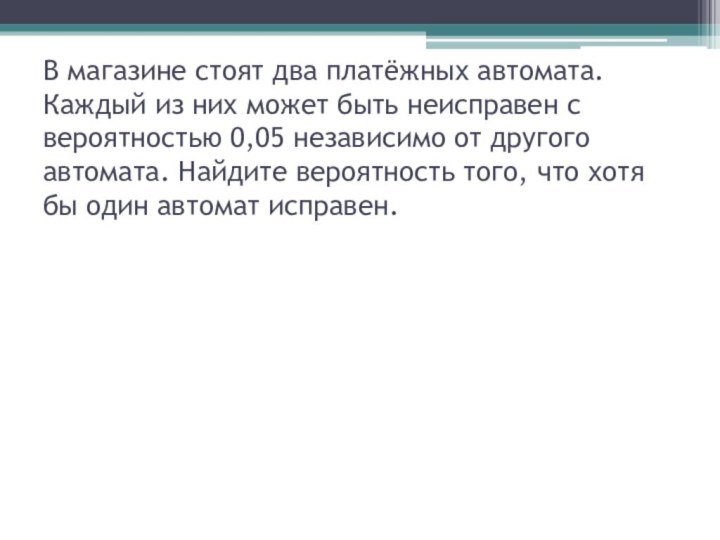
- 28. В магазине стоят два платёжных автомата. Каждый
- 29. В магазине стоят два платёжных автомата. Каждый
- 30. Вероятность того, что на тестировании по биологии
- 31. Вероятность того, что на тестировании по биологии
- 32. Стрелок стреляет по мишени один раз. В
- 33. Стрелок стреляет по мишени один раз. В
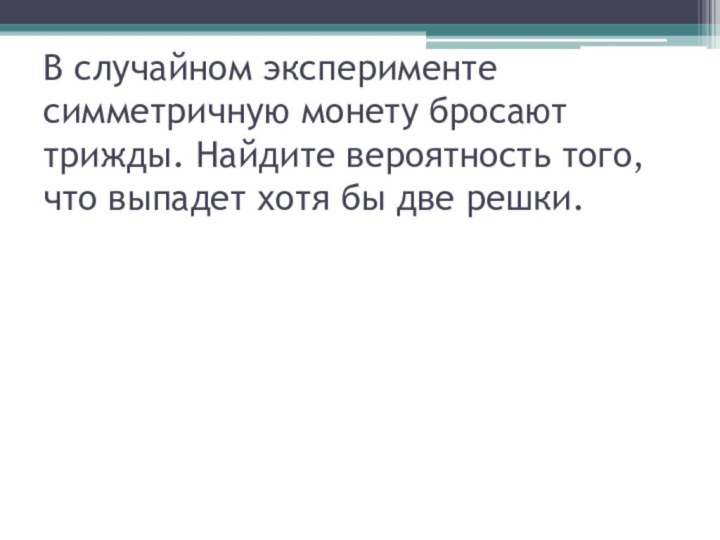
- 34. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
- 35. В случайном эксперименте симметричную монету бросают трижды.
- 36. Перед началом волейбольного матча капитаны команд тянут
- 37. Перед началом волейбольного матча капитаны команд тянут
- 38. Две фабрики выпускают одинаковые стекла для автомобильных
- 39. Две фабрики выпускают одинаковые стекла для автомобильных
- 40. На экзамене по геометрии школьник отвечает на
- 41. На экзамене по геометрии школьник отвечает на
- 42. При изготовлении подшипников диаметром 67 мм вероятность
- 43. При изготовлении подшипников диаметром 67 мм вероятность
- 44. Вероятность того, что в случайный момент времени
- 45. Вероятность того, что в случайный момент времени
- 46. В магазине три продавца. Каждый из них
- 47. В магазине три продавца. Каждый из них
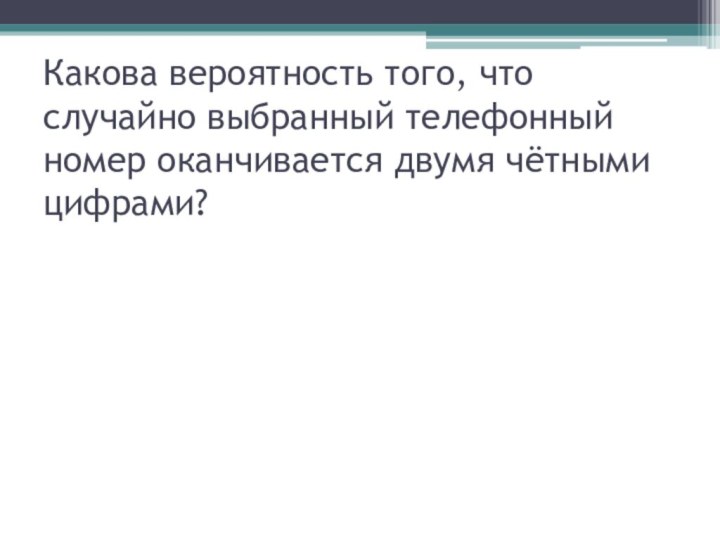
- 48. Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
- 49. Какова вероятность того, что случайно выбранный телефонный
- 50. Если шахматист А. играет белыми фигурами, то
- 51. Скачать презентацию
- 52. Похожие презентации














































Слайд 3 На экзамен вынесено 60 вопросов, Андрей не выучил
3 из них. Найдите вероятность того, что ему попадется
выученный вопрос. Андрей выучил 60 – 3 = 57 вопросов. Поэтому вероятность того, что на экзамене ему попадется выученный вопрос равна
Ответ: 0,95.
Слайд 4 В фирме такси в данный момент свободно 20
машин: 10 черных, 2 желтых и 8 зеленых. По
вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.Слайд 5 В фирме такси в данный момент свободно 20
машин: 10 черных, 2 желтых и 8 зеленых. По
вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Вероятность того, что к заказчице приедет зеленое такси равна

Ответ: 0,4.
Слайд 6 В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 8 очков. Результат
округлите до сотых.Слайд 7 В случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 8 очков. Результат
округлите до сотых. Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна

Ответ: 0,14.
Слайд 8 В случайном эксперименте симметричную монету бросают дважды. Найдите
вероятность того, что орел выпадет ровно один раз.
Слайд 9 В случайном эксперименте симметричную монету бросают дважды. Найдите
вероятность того, что орел выпадет ровно один раз.
Равновозможны 4 исхода эксперимента: орел-орел, орел-решка, решка-орел, решка-решка. Орел выпадает ровно один раз в двух случаях: орел-решка и решка-орел. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна
Ответ: 0,5.
Слайд 10 При производстве в среднем на каждые 2982 исправных
насоса приходится 18 неисправных. Найдите вероятность того, что случайно
выбранный насос окажется неисправным.Слайд 11 При производстве в среднем на каждые 2982 исправных
насоса приходится 18 неисправных. Найдите вероятность того, что случайно
выбранный насос окажется неисправным. В среднем неисправны 18 из каждых 3000 насосов, поэтому вероятность случайно выбрать неисправный насос равна
Ответ: 0,006.
Слайд 12 Научная конференция проводится в 5 дней. Всего запланировано
75 докладов — первые три дня по 17 докладов,
остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?Слайд 13 Научная конференция проводится в 5 дней. Всего запланировано
75 докладов — первые три дня по 17 докладов,
остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? За первые три дня будет прочитан 51 доклад, на последние два дня планируется 24 доклада. Поэтому на последний день запланировано 12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 
Ответ: 0,16.
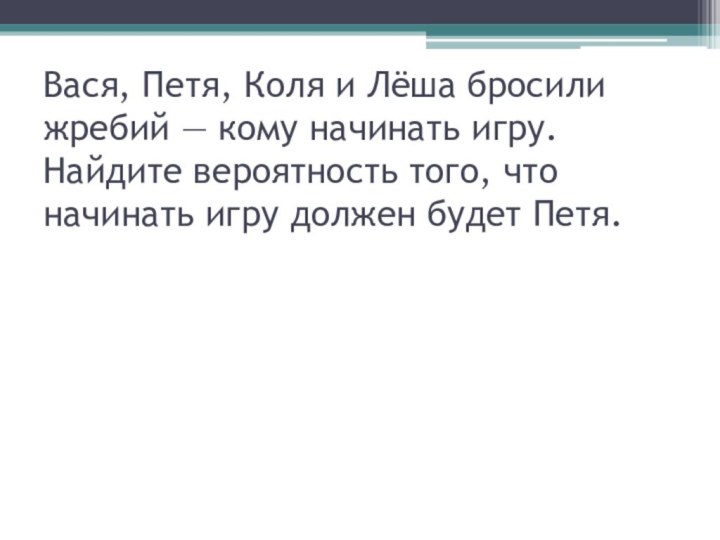
Слайд 14 Вася, Петя, Коля и Лёша бросили жребий —
кому начинать игру. Найдите вероятность того, что начинать игру
должен будет Петя.Слайд 15 Вася, Петя, Коля и Лёша бросили жребий —
кому начинать игру. Найдите вероятность того, что начинать игру
должен будет Петя. Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это будет именно Петя, равна одной четвертой.
Ответ: 0,25.
Слайд 16 Перед началом футбольного матча судья бросает монетку, чтобы
определить, какая из команд начнёт игру с мячом. Команда
«Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.Слайд 17 Перед началом футбольного матча судья бросает монетку, чтобы
определить, какая из команд начнёт игру с мячом. Команда
«Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Ответ: 0,375.
Слайд 18 Если шахматист А. играет белыми фигурами, то он
выигрывает у шахматиста Б. с вероятностью 0,5. Если А.
играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.Слайд 19 Если шахматист А. играет белыми фигурами, то он
выигрывает у шахматиста Б. с вероятностью 0,5. Если А.
играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,3 = 0,15.
Ответ: 0,15.
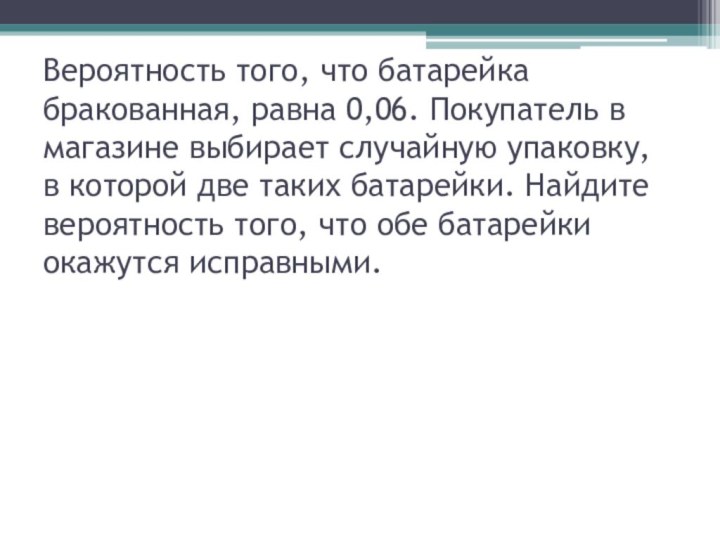
Слайд 20 Вероятность того, что батарейка бракованная, равна 0,06. Покупатель
в магазине выбирает случайную упаковку, в которой две таких
батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.Слайд 21 Вероятность того, что батарейка бракованная, равна 0,06. Покупатель
в магазине выбирает случайную упаковку, в которой две таких
батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. Вероятность того, что батарейка исправна, равна 0,94. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,94·0,94 = 0,8836.
Ответ: 0,8836.
Слайд 22 Вероятность того, что новый электрический чайник прослужит больше
года, равна 0,93. Вероятность того, что он прослужит больше
двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.Слайд 23 Вероятность того, что новый электрический чайник прослужит больше
года, равна 0,93. Вероятность того, что он прослужит больше
двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,93 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем:
P(A) = 0,93 − 0,87 = 0,06.
Ответ: 0,06.
Слайд 24 Из районного центра в деревню ежедневно ходит автобус.
Вероятность того, что в понедельник в автобусе окажется меньше
18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.Слайд 25 Из районного центра в деревню ежедневно ходит автобус.
Вероятность того, что в понедельник в автобусе окажется меньше
18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17. Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31.
Ответ: 0,31.
Слайд 26 Помещение освещается фонарём с двумя лампами. Вероятность перегорания
лампы в течение года равна 0,3. Найдите вероятность того,
что в течение года хотя бы одна лампа не перегорит.Слайд 27 Помещение освещается фонарём с двумя лампами. Вероятность перегорания
лампы в течение года равна 0,3. Найдите вероятность того,
что в течение года хотя бы одна лампа не перегорит. Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Ответ: 0,91.
Слайд 28 В магазине стоят два платёжных автомата. Каждый из
них может быть неисправен с вероятностью 0,05 независимо от
другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.Слайд 29 В магазине стоят два платёжных автомата. Каждый из
них может быть неисправен с вероятностью 0,05 независимо от
другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975.
Ответ: 0,9975.
Слайд 30 Вероятность того, что на тестировании по биологии учащийся
О. верно решит больше 11 задач, равна 0,67. Вероятность
того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.Слайд 31 Вероятность того, что на тестировании по биологии учащийся
О. верно решит больше 11 задач, равна 0,67. Вероятность
того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
Ответ: 0,07.
Слайд 32 Стрелок стреляет по мишени один раз. В случае
промаха стрелок делает второй выстрел по той же мишени.
Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).Слайд 33 Стрелок стреляет по мишени один раз. В случае
промаха стрелок делает второй выстрел по той же мишени.
Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом). Пусть событие А состоит в том, что цель поражена с первого выстрела, В — со второго. Вероятность того, что мишень будет поражена первым или вторым выстрелом равна вероятности суммы событий A и B. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,7 + 0,7 − 0,49 = 0,91.
Слайд 34 В случайном эксперименте симметричную монету бросают трижды. Найдите
вероятность того, что выпадет хотя бы две решки.
Слайд 35 В случайном эксперименте симметричную монету бросают трижды. Найдите
вероятность того, что выпадет хотя бы две решки.
Всего возможных исходов — 8: орел-орел-орел, орел-орел-решка, орел-решка-решка, орел-решка-орел, решка-решка-решка, решка-решка-орел, решка-орел-орел, решка-орел-решка. Благоприятными являются четыре: решка-решка-решка, решка-решка-орел, решка-орел-решка, орел-решка-решка. Следовательно, искомая вероятность равна 4 : 8 = 0,5.Ответ: 0,5.
Слайд 36 Перед началом волейбольного матча капитаны команд тянут честный
жребий, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.Слайд 37 Перед началом волейбольного матча капитаны команд тянут честный
жребий, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.
Ответ: 0,125.
Слайд 38 Две фабрики выпускают одинаковые стекла для автомобильных фар.
Первая фабрика выпускает 45% этих стекол, вторая — 55%.
Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.Слайд 39 Две фабрики выпускают одинаковые стекла для автомобильных фар.
Первая фабрика выпускает 45% этих стекол, вторая — 55%.
Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.
Слайд 40 На экзамене по геометрии школьник отвечает на один
вопрос из списка экзаменационных вопросов. Вероятность того, что это
вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.Слайд 41 На экзамене по геометрии школьник отвечает на один
вопрос из списка экзаменационных вопросов. Вероятность того, что это
вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.
Ответ: 0,35.
Слайд 42 При изготовлении подшипников диаметром 67 мм вероятность того,
что диаметр будет отличаться от заданного не больше, чем
на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.Слайд 43 При изготовлении подшипников диаметром 67 мм вероятность того,
что диаметр будет отличаться от заданного не больше, чем
на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Ответ: 0,035.
Слайд 44 Вероятность того, что в случайный момент времени температура
тела здорового человека окажется ниже чем 36,8 °С, равна
0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или вышеСлайд 45 Вероятность того, что в случайный момент времени температура
тела здорового человека окажется ниже чем 36,8 °С, равна
0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19.
Ответ: 0,19.
Слайд 46 В магазине три продавца. Каждый из них занят
с клиентом с вероятностью 0,3. Найдите вероятность того, что
в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).Слайд 47 В магазине три продавца. Каждый из них занят
с клиентом с вероятностью 0,3. Найдите вероятность того, что
в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга). Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна 
Ответ: 0,027.
Слайд 48 Какова вероятность того, что случайно выбранный телефонный номер
оканчивается двумя чётными цифрами?
Слайд 49 Какова вероятность того, что случайно выбранный телефонный номер
оканчивается двумя чётными цифрами?
Вероятность того, что на
одном из требуемых мест окажется чётное число равна 0,5. Следовательно, вероятность того, что на двух местах одновременно окажутся два чётных числа равна 0,5 · 0,5 = 0,25.Ответ: 0,25.