Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике на тему Решение уравнений и неравенств при подготовке к ЕГЭ

Содержание

УравненияУравнением называется равенство, содержащее неизвестное, обозначаемое буквой. Пользуясь понятием функции, можно сказать, что уравнение (с одним неизвестным) - это пара функций от одной и той же переменной x, соединенных знаком равенства:
Решение уравнений и неравенствРаботу выполнили: Бабушкина К. Карпикова К. Ковязина О. УравненияУравнением называется равенство, содержащее неизвестное, обозначаемое буквой. Пользуясь понятием функции, можно сказать, Областью допустимых значений (ОДЗ) данного уравнения называется пересечение области определения функций f(x) Решить уравнение - это значит найти все его корни или доказать, что Решение уравнения Системы уравнений с двумя неизвестнымиУравнением с двумя неизвестными x и y называется Системой двух уравнений с двумя неизвестными называется пара уравнений с двумя неизвестными: Системы линейных уравненийПусть дана система a1x+b1y=c1 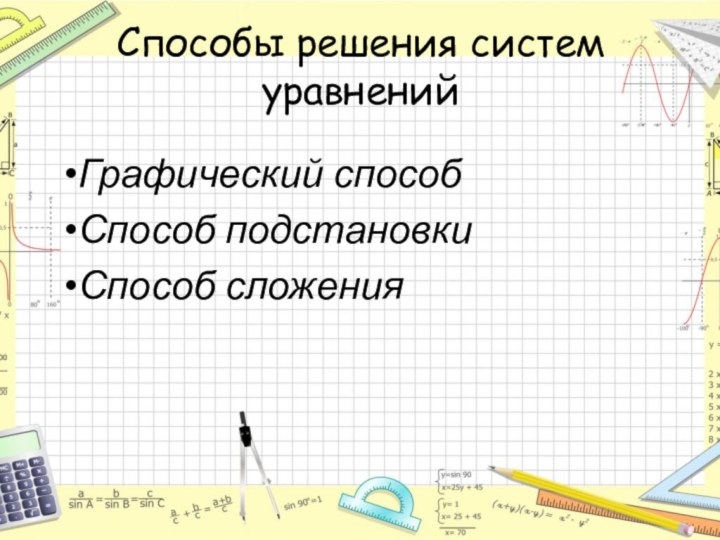Способы решения систем уравненийГрафический способСпособ подстановкиСпособ сложения Графический способЧтобы решить графическим способом систему двух уравнений с двумя переменными, нужно 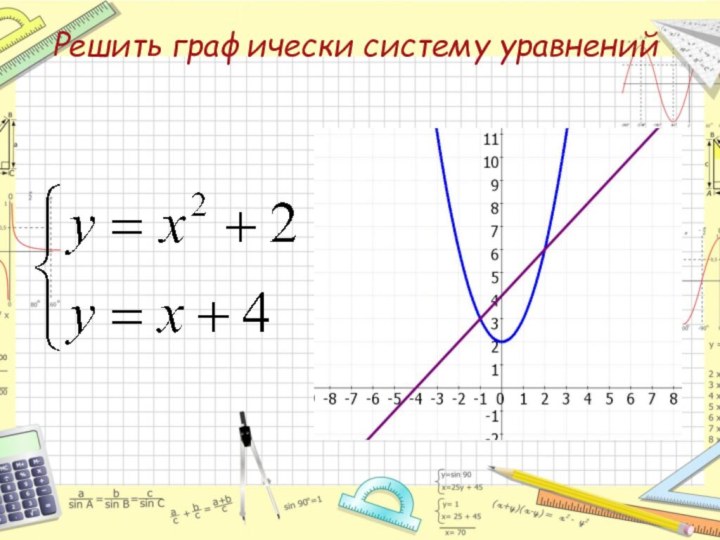Решить графически систему уравнений Способ ПодстановкиЗаключается в том , что в одном из уравнений выражают одну Решить систему уравнений способом подстановки7х -2·(4+2x) = 317x - 8- 4x = Способ сложения Заключается в том, что если данная система состоит из уравнений, Решить систему уравнений способом сложения4х - 7·30 = 304x - 210 = Решение системы уравнений Решаем первое уравнение: перенесем z в правую часть и возведем обе части Вычтем из уравнения (1) второе уравнение системы, умноженное на 2:(x2 + 2xy Получим: x – y = 0 НеравенстваНеравенством с одним неизвестным называется пара функций от одной и той же Решить неравенство (систему неравенств) значит найти множество всех решений этого неравенства (этой Отметим, что проверка правильности всех найденных решений неравенства подстановкой в исходные неравенства В противном случае нахождение ОДЗ обязательно. При этом возможны два подхода к Решить систему неравенствВ ответ запишите сумму целых решений. Решим оба неравенства системы методом интервалов.Решением этого неравенства является объединение промежутков Аналогично получим, что решением неравенства Нанесем оба решения на одну числовую ось (сверху решение первого, снизу второго):Пересечение Объединение неравенствОтметим также, что очень часто решениями данного неравенства(системы неравенств) является объединение Эту запись будем называть объединением неравенств. Решением объединения двух неравенств является всякое Решить объединение неравенствВ ответ запишите наибольшее целое решение. Решаем первое неравенство. Разложим числитель левой части на множители, используя формулу разложения квадратного трехчлена на множители. Умножим обе части на (-1), знак неравенства изменится на противоположный:Квадратный трехчлен х2+х+2>0, Если умножить на него левую и правую часть неравенства, то получим равносильное Решаем второе неравенство.Рассуждая также, как и в первом неравенстве, приходим к выводу, Получим неравенство:х2 Значит, второе неравенство совокупности решений не имеет. 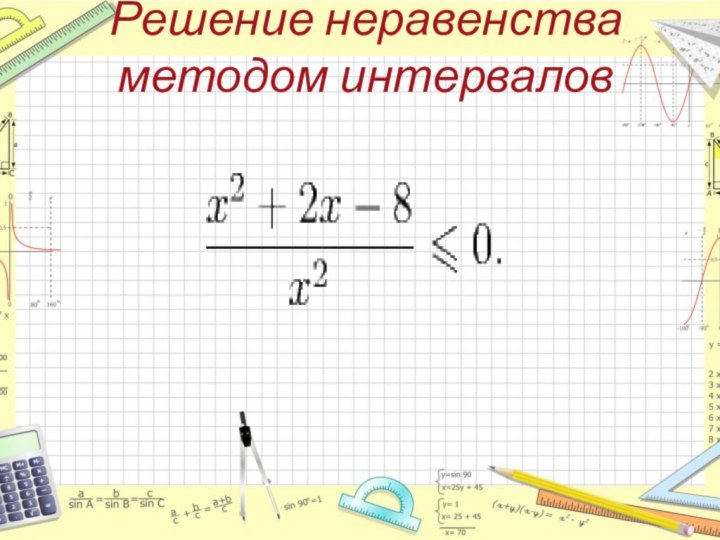Поэтому решение совокупности совпадает с Рациональные неравенстваРациональным называется всякое неравенство, сводящееся к неравенству вида Поскольку При преобразованиях выражений и, в частности, при разложении их на множители иногда помогают формулы сокращенного умножения: Решение неравенства методом интервалов Разложим числитель левой части неравенства на скобки. Для этого найдем решения уравнения x2 Найдем нули числителя и знаменателя: x1 = -4, x2= 2, x3 Расставим знаки на каждом интервале, с учетом того, что x2 всегда больше Показательные уравнения и неравенстваСтандартный способ решения простейших показательных уравнений и неравенств основывается Если же основание a удовлетворяет неравенствам 0 Для приведения исходного показательного уравнения или неравенства к нужному виду могут пригодится К неравенствам вида (af-ag)xh˅0 применим метод замены множителя, позволяющий сильно упростить выражение 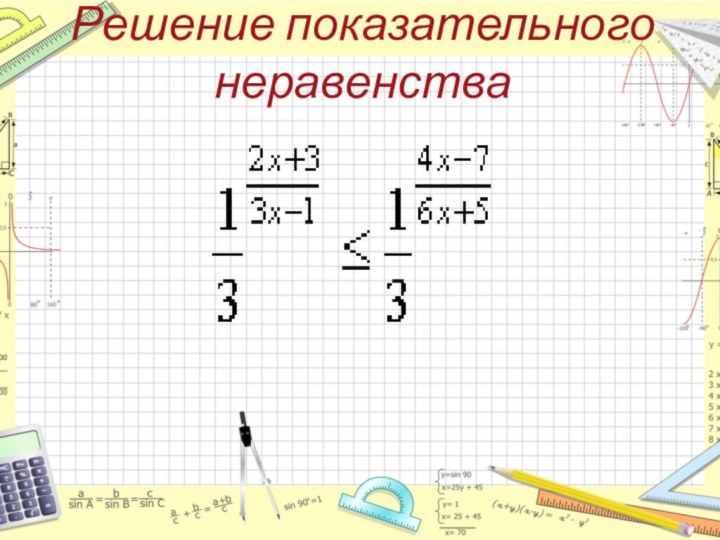Решение показательного неравенства Так как основание меньше единицы, но больше нуля, то наше неравенство эквивалентно неравенству: Перенесем все в левую часть, приведем к общему знаменателю. Решим неравенство методом интервалов, получим ответ: Логарифмические уравнения и неравенстваСтандартный метод решения простейших логарифмических уравнений и неравенств опирается В случае 0 Для того чтобы отбросить логарифмы в уравнении или неравенстве Для приведения исходного логарифмического уравнения или неравенства к нужному виду могут пригодиться Решение логарифмического уравненияlog x – 1 25 = 2 ОДЗ:Х – 1 ≠ 1 К неравенствам вида Опять же, в случае 00. Решение логарифмического неравенства Иррациональные уравнения и неравенстваДля избавления от радикалов в иррациональных уравнениях или неравенствах Пусть f,g≥0, тогда уравнение или неравенство f ˅ g равносильно уравнению или Преобразования иррациональных уравнений или неравенств производится по следующим формулам действий с арифметическими Корни четной степени извлекаются только из неотрицательных чисел. Поэтому, действуя по приведенным Решение иррационального уравнения К неравенствам вида Решение иррационального неравенства ОДЗ:Заметим, что в ОДЗ x ≥ 0, поэтому существует и значит  Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, Имеем:С учетом ОДЗ получаем ответ: Уравнения и неравенства с модулемСтандартное правило раскрытия модуля основывается на его определении: Раскрывая сразу несколько модулей, приходится разбирать случаи, которые задаются знаками выражений, стоящих Другой подход , напоминающий скорее не раскрытие, а отбрасывание модулей, применим к Исходя из этого смысла, можно установить справедливость, например, таких утверждений:уравнение |f|=|g| равносильно Полезную роль при преобразовании выражений могут сыграть следующие свойства модулей: К неравенствам вида (|f|-|g|)xh˅0 также применим метод замены множителя: множитель |f|-|g| можно Решение уравнения с модулем│x - 1│- 2 │x + 2│= 0 Найдем точки перемены знака модуля из условий: На промежутке (- ∞; -2 ] уравнение имеет вид:( – х + На промежутке [-2;1] уравнение имеет вид:( – х + 1 ) – На промежутке [1;+∞) уравнение имеет вид:( х – 1 ) – Решение неравенства с модулем Как видно, найти значения x, при которых подмодульное выражение обращается в нуль,
Слайды презентации

Слайд 2 Уравнения
Уравнением называется равенство, содержащее неизвестное, обозначаемое буквой. Пользуясь

УравненияУравнением называется равенство, содержащее неизвестное, обозначаемое буквой. Пользуясь понятием функции, можно

понятием функции, можно сказать, что уравнение (с одним неизвестным)

- это пара функций от одной и той же переменной x, соединенных знаком равенства: f(x)=g(x)

Слайд 3 Областью допустимых значений (ОДЗ) данного уравнения называется пересечение

Областью допустимых значений (ОДЗ) данного уравнения называется пересечение области определения функций

области определения функций f(x) и g(x):

D(f)∩D(g)
Число a называется корнем(или решением) данного уравнения, если при подстановке в уравнение вместо каждого вхождения x числа a уравнение обращается в верное числовое равенство: f(a)=g(a).

Слайд 4 Решить уравнение - это значит найти все его

Решить уравнение - это значит найти все его корни или доказать,

корни или доказать, что данное уравнение корней не имеет.
Два

уравнения называются равносильными, если множества их корней совпадают. Уравнение A является следствием уравнения B, если все корни уравнения B являются корнями уравнения A (но, быть может, среди корней уравнения A есть такие, которые не являются корнями B).

Слайд 5 Решение уравнения

Решение уравнения

Слайд 6 Системы уравнений с двумя неизвестными
Уравнением с двумя неизвестными

Системы уравнений с двумя неизвестнымиУравнением с двумя неизвестными x и y

x и y называется пара функций от двух переменных

(x и y), соединенных знаком равенства: f(x0, y0)=g(x0, y0)
Решением такого уравнения называется всякая пара чисел (x0, y0), подстановка которых в уравнение вместо соответствующих неизвестных обращает это уравнение в верное равенство.

Слайд 7 Системой двух уравнений с двумя неизвестными называется пара

Системой двух уравнений с двумя неизвестными называется пара уравнений с двумя

уравнений с двумя неизвестными:

Решением системы называется пара чисел (x0,

y0), являющаяся решением и первого, и второго уравнений системы.
Решить систему - это значит найти все её решения или доказать, что система решений не имеет.

Слайд 8 Системы линейных уравнений
Пусть дана система

Системы линейных уравненийПусть дана система a1x+b1y=c1

a1x+b1y=c1

a2x+b2y=c2
Система имеет единственное решение тогда и только тогда, когда a1b2-a2b1≠0;
Система имеет бесконечное множество решений тогда и только тогда, когда a1b2-a2b1=0 a1c2-a2c1=0 b1c2-b2c1=0
Система не имеет решений тогда и только тогда, когда a1b2-a2b1=0, но a1c2-a2c1≠0 или b1c2-b2c1≠0.

Слайд 9 Способы решения систем уравнений
Графический способ
Способ подстановки
Способ сложения

Способы решения систем уравненийГрафический способСпособ подстановкиСпособ сложения

Слайд 10 Графический способ
Чтобы решить графическим способом систему двух уравнений

Графический способЧтобы решить графическим способом систему двух уравнений с двумя переменными,

с двумя переменными, нужно построить график каждого из уравнений

системы и найти их точки пересечения.
Координаты каждой точки образуют решение системы.
Сколько точек пересечения -столько решений имеет система.

Слайд 11 Решить графически систему уравнений

Решить графически систему уравнений

Слайд 12 Способ Подстановки
Заключается в том , что в одном

Способ ПодстановкиЗаключается в том , что в одном из уравнений выражают

из уравнений выражают одну переменную через другую. Полученное выражение

подставляют в другое уравнение, которое после этого обращается в уравнение с одной переменной, а затем решают его. Получившиеся значения подставляют в любое уравнение исходной системы и находят вторую переменную.

Слайд 13 Решить систему уравнений способом подстановки
7х -2·(4+2x) = 31
7x

Решить систему уравнений способом подстановки7х -2·(4+2x) = 317x - 8- 4x

- 8- 4x = 31
3x = 39
x = 13
y

= 4 + 2·13

y = 30

Ответ : (13; 30)

Слайд 14 Способ сложения
Заключается в том, что если данная

Способ сложения Заключается в том, что если данная система состоит из

система состоит из уравнений, которые при почленном сложении образуют

уравнение с одной переменной, то, решив это уравнение, мы получим значения одной из переменных. Значения второй переменной находятся как и в способе подстановки.

Слайд 15 Решить систему уравнений способом сложения
4х - 7·30 =

Решить систему уравнений способом сложения4х - 7·30 = 304x - 210

30
4x - 210 = 30
4x = 240
x

= 60

2y = 60
y = 30

Ответ: (60;30)

Слайд 16 Решение системы уравнений

Решение системы уравнений

Слайд 17 Решаем первое уравнение: перенесем z в правую часть

Решаем первое уравнение: перенесем z в правую часть и возведем обе

и возведем обе части в квадрат

x + y =

4 – z,
(x + y)2 = (4 – z)2,
x2 + 2xy + y2 = 16 – 8z + z2 (1)

Слайд 18 Вычтем из уравнения (1) второе уравнение системы, умноженное

Вычтем из уравнения (1) второе уравнение системы, умноженное на 2:(x2 +

на 2:

(x2 + 2xy + y2) – 2·(2xy –

z2) = (16 – 8z + z2) – 2·16
x2 + 2xy + y2 – 4xy + 2z2 = 16 – 8z + z2 – 32,
x2 – 2xy + y2 + z2 + 8z + 16 = 0,
(x – y)2 + (z + 4)2 = 0

Квадрат любого числа больше либо равен нулю. Поэтому сумма двух квадратов равна нулю только в том случае, если каждый из них равен нулю.


Слайд 19 Получим:
x – y = 0

Получим: x – y = 0

z + 4 = 0 x = y z = -4
Подставим эти выражения в первое уравнение системы: x + y + z = 4
 y + y – 4 = 4
 2y = 8
 y = 4
 x = 4

Ответ: (4; 4;- 4)

Слайд 20 Неравенства
Неравенством с одним неизвестным называется пара функций от

НеравенстваНеравенством с одним неизвестным называется пара функций от одной и той

одной и той же переменной, соединенная одним из знаков:

>,≥,<,≤,≠.
Решением неравенства (системы неравенств) называется всякое действительное число, подстановка которого в неравенство (каждое неравенство системы) вместо каждого вхождения неизвестного (переменной) обращает это неравенство (все неравенства системы) в верное числовое неравенство (верные числовые неравенства).

Слайд 21 Решить неравенство (систему неравенств) значит найти множество всех

Решить неравенство (систему неравенств) значит найти множество всех решений этого неравенства

решений этого неравенства (этой системы неравенств) или доказать, что

оно (она) решений не имеет. Два неравенства (две системы неравенств) называются равносильными, если множества их решений совпадают. Соответственно, преобразования неравенства называются равносильными, если при этих преобразованиях множество решений полученного неравенства совпадает с множеством решений исходного неравенства.

Слайд 22 Отметим, что проверка правильности всех найденных решений неравенства

Отметим, что проверка правильности всех найденных решений неравенства подстановкой в исходные

подстановкой в исходные неравенства в подавляющем большинстве случаев невозможна.

Поэтому при решении неравенств (систем неравенств) нужно пользоваться равносильными преобразованиями (равносильными преобразованиями в рамках ОДЗ). Нахождение ОДЗ не обязательно, если вы пользуетесь исключительно равносильными преобразованиями.

Слайд 23 В противном случае нахождение ОДЗ обязательно. При этом

В противном случае нахождение ОДЗ обязательно. При этом возможны два подхода

возможны два подхода к оформлению решения:
ОДЗ в виде

неравенства или системы неравенств присоединяют к данному неравенству (данной системе) и полученную систему решают;
Находят ОДЗ. Решают данное неравенство(систему неравенств), пользуясь лишь равносильными преобразованиями в рамках ОДЗ. Из полученных решений удаляют те, которые не входят в ОДЗ.

Слайд 24 Решить систему неравенств
В ответ запишите сумму целых решений.

Решить систему неравенствВ ответ запишите сумму целых решений.

Слайд 25 Решим оба неравенства системы методом интервалов.
Решением этого неравенства

Решим оба неравенства системы методом интервалов.Решением этого неравенства является объединение промежутков

является объединение промежутков

Слайд 26 Аналогично получим, что решением неравенства

Аналогично получим, что решением неравенства

является отрезок [-2;6].

Решением системы неравенств с одной переменной будет пересечение решений всех неравенств системы.


Слайд 27 Нанесем оба решения на одну числовую ось (сверху

Нанесем оба решения на одну числовую ось (сверху решение первого, снизу

решение первого, снизу второго):

Пересечение решений это те точки на

оси, у которых имеется двойная штриховка (снизу и сверху). Это множество, состоящее из числа -2 и отрезка [2;6].
В этом множестве содержатся целые числа: -2, 2, 3, 4, 5 и 6. Их сумма равна 18.
Ответ: 18

Слайд 28 Объединение неравенств
Отметим также, что очень часто решениями данного

Объединение неравенствОтметим также, что очень часто решениями данного неравенства(системы неравенств) является

неравенства(системы неравенств) является объединение решений двух или более неравенств(систем

неравенств). В таких случаях мы будем употреблять запись вида f(x)≥g(x) h(x)

Слайд 29 Эту запись будем называть объединением неравенств. Решением объединения

Эту запись будем называть объединением неравенств. Решением объединения двух неравенств является

двух неравенств является всякое число, являющееся решением хотя бы

одного из двух неравенств объединения. Иначе говоря, для решения объединения нужно найти множества всех решений первого и второго неравенств и найденные множества объединить.

Слайд 30 Решить объединение неравенств
В ответ запишите наибольшее целое решение.

Решить объединение неравенствВ ответ запишите наибольшее целое решение.

Слайд 31 Решаем первое неравенство. Разложим числитель левой части на

Решаем первое неравенство. Разложим числитель левой части на множители, используя формулу разложения квадратного трехчлена на множители.

множители, используя формулу разложения квадратного трехчлена на множители.

Слайд 32 Умножим обе части на (-1), знак неравенства изменится

Умножим обе части на (-1), знак неравенства изменится на противоположный:Квадратный трехчлен

на противоположный:
Квадратный трехчлен х2+х+2>0, т.к. отрицательный дискриминант и положительный

старший коэффициент (число, стоящее перед х2).

Слайд 33 Если умножить на него левую и правую часть

Если умножить на него левую и правую часть неравенства, то получим

неравенства, то получим равносильное неравенство:
Решив его методом интервалов, получим

ответ:

Слайд 34 Решаем второе неравенство.
Рассуждая также, как и в первом

Решаем второе неравенство.Рассуждая также, как и в первом неравенстве, приходим к

неравенстве, приходим к выводу, что х2 + x +

1 > 0 для всех х и на него можно умножить левую и правую части неравенства.

Слайд 35 Получим неравенство:
х2

Получим неравенство:х2

квадрат любого числа неотрицательный.

Слайд 36 Значит, второе неравенство совокупности решений не имеет. Поэтому

Значит, второе неравенство совокупности решений не имеет. Поэтому решение совокупности совпадает

решение совокупности совпадает с решением первого неравенства:

Наибольшее целое

решение — число 3.

Ответ: 3.

Слайд 37 Рациональные неравенства
Рациональным называется всякое неравенство, сводящееся к неравенству

Рациональные неравенстваРациональным называется всякое неравенство, сводящееся к неравенству вида

вида

или вида ,

где P(x), Q(x) - некоторые многочлены.

Слайд 38 Поскольку

Поскольку







то для решения рациональных неравенств удобно применять метод интервалов.

Слайд 39 При преобразованиях выражений и, в частности, при разложении

При преобразованиях выражений и, в частности, при разложении их на множители иногда помогают формулы сокращенного умножения:

их на множители иногда помогают формулы сокращенного умножения:

Слайд 40 Решение неравенства методом интервалов

Решение неравенства методом интервалов

Слайд 41 Разложим числитель левой части неравенства на скобки.
Для

Разложим числитель левой части неравенства на скобки. Для этого найдем решения

этого найдем решения уравнения

 x2 + 2x - 8 =

0
x1 = -4, x2 = 2.

Мы получим разложение на множители:
x2 + 2x - 8 = (x + 4)(x - 2).


Слайд 42 Найдем нули числителя и знаменателя: x1 = -4,

Найдем нули числителя и знаменателя: x1 = -4, x2= 2, x3

x2= 2, x3 = 0.

Нанесем эти числа на ось,

при этом нули знаменателя будут выколотыми точками, а нули числителя нет.

Слайд 43 Расставим знаки на каждом интервале, с учетом того,

Расставим знаки на каждом интервале, с учетом того, что x2 всегда

что x2 всегда больше или равен нуля. В результате

должно получиться то, что изображено на рисунке выше.
Поскольку знак неравенства ≤, то мы выбираем те интервалы, над которыми стоит знак "-".
Записываем решение неравенства

Слайд 44 Показательные уравнения и неравенства
Стандартный способ решения простейших показательных

Показательные уравнения и неравенстваСтандартный способ решения простейших показательных уравнений и неравенств

уравнений и неравенств основывается на монотонности показательной функции, из

которой получается следующее основное правило отбрасывания оснований: пусть a>1, тогда уравнение или неравенство af ˅ ag равносильно уравнению или неравенству f ˅ g, где ˅ - это >,≥,<,≤.
В этом правиле последнее уравнение или неравенство имеет тот же знак ˅, что и первое, так как показательная функция с основанием a>1 возрастает.

Слайд 45 Если же основание a удовлетворяет неравенствам 0

Если же основание a удовлетворяет неравенствам 0

в сформулированный переход необходимо внести поправку, поменяв в конце

знак на обратный, а именно: > на <, знак ≥ на ≤ и.т.д., но знак = (как и знак ≠) при этом не меняется вовсе. Все дело в том, что показательная функция с основанием, меньшим единицы, уже не возрастает, а убывает.

Слайд 46 Для приведения исходного показательного уравнения или неравенства к

Для приведения исходного показательного уравнения или неравенства к нужному виду могут

нужному виду могут пригодится следующие формулы действий со степенями(a,

b>0):

Слайд 47 К неравенствам вида (af-ag)xh˅0 применим метод замены множителя,

К неравенствам вида (af-ag)xh˅0 применим метод замены множителя, позволяющий сильно упростить

позволяющий сильно упростить выражение в скобках и состоящий в

следующем: пусть a>1, тогда множитель af-ag можно заменить множителем f-g того же знака.
При указанной замене сохраняется каждое из трех возможных событий: положительность множителя, его отрицательность и равенство его нулю. В случае 0

Слайд 48 Решение показательного неравенства

Решение показательного неравенства

Слайд 49 Так как основание меньше единицы, но больше нуля,

Так как основание меньше единицы, но больше нуля, то наше неравенство эквивалентно неравенству:

то наше неравенство эквивалентно неравенству:

Слайд 50 Перенесем все в левую часть, приведем к общему

Перенесем все в левую часть, приведем к общему знаменателю. Решим неравенство методом интервалов, получим ответ:

знаменателю. Решим неравенство методом интервалов, получим ответ:

Слайд 51 Логарифмические уравнения и неравенства
Стандартный метод решения простейших логарифмических

Логарифмические уравнения и неравенстваСтандартный метод решения простейших логарифмических уравнений и неравенств

уравнений и неравенств опирается на монотонность логарифмической функции, т.е.

на следующее основное правило отбрасывания логарифмов: пусть a>1, тогда уравнение или неравенство равносильно системе:

Слайд 52 В случае 0

В случае 0

системе необходимо заменить неравенством f ˄ g, так как

логарифмическая функция с таким основанием a убывает.
Если же основание логарифма не есть константа, то отдельно разбираются случаи, когда оно больше единицы и когда меньше.

Слайд 53 Для того чтобы отбросить логарифмы в уравнении или

Для того чтобы отбросить логарифмы в уравнении или неравенстве

неравенстве

, его правую часть можно представить в нужном виде с помощью тождества:

Слайд 54 Для приведения исходного логарифмического уравнения или неравенства к

Для приведения исходного логарифмического уравнения или неравенства к нужному виду могут

нужному виду могут пригодиться следующие формулы действий с логарифмами(a,

b, x, y>0 и a, b≠1):

Слайд 55 Решение логарифмического уравнения
log x – 1 25 =

Решение логарифмического уравненияlog x – 1 25 = 2

Слайд 56 ОДЗ:
Х – 1 ≠ 1

ОДЗ:Х – 1 ≠ 1 Х

Х ≠

2
Х – 1 > 0 Х > 1

Воспользуемся основным логарифмическим тождеством:
 (x – 1)2= 25
Х2 – 2х + 1 = 25
Х2 – 2х – 24 = 0
Х1=6 Х2=-4 (не принадлежит ОДЗ)

Слайд 57 К неравенствам вида

К неравенствам вида

также применим метод замены множителя: пусть a>1 тогда множитель можно заменить множителем f-g того же знака при дополнительных условиях a, f, g>0 и a≠1.
Важный частный случай этой замены получается при подстановке в ней g=1:пусть a>1, тогда множитель можно заменить множителем f-1 при f>0.

Слайд 58 Опять же, в случае 0

Опять же, в случае 00.

можно

заменить противоположным множителем g-f при g, f, a>0 и a≠1, а множитель -противоположным множителем 1-f при f>0.

Слайд 59 Решение логарифмического неравенства

Решение логарифмического неравенства

Слайд 60

Слайд 61

Слайд 62

Слайд 63 Иррациональные уравнения и неравенства
Для избавления от радикалов в

Иррациональные уравнения и неравенстваДля избавления от радикалов в иррациональных уравнениях или

иррациональных уравнениях или неравенствах требуется, прежде всего, умение возводить

обе части в квадрат. Делается это с помощью следующего основного правила возведения в квадрат, базирующегося на возрастании простейшей квадратичной функции на положительной полуоси.

Слайд 64 Пусть f,g≥0, тогда уравнение или неравенство f ˅

Пусть f,g≥0, тогда уравнение или неравенство f ˅ g равносильно уравнению

g равносильно уравнению или неравенству f2 ˅ g2.
Это

правило не распространяется на те случаи, в которых хотя бы одна из частей уравнения или неравенства отрицательна, - их нужно рассматривать отдельно.
Что же касается возведения в квадрат неравенств, то тут ситуация гораздо серьезнее: несоблюдение основного правила может привести как к приобретению, так и к потере решений.

Слайд 65 Преобразования иррациональных уравнений или неравенств производится по следующим

Преобразования иррациональных уравнений или неравенств производится по следующим формулам действий с

формулам действий с арифметическими корнями

(x, y≥0;n, m N и k Z):

Слайд 66 Корни четной степени извлекаются только из неотрицательных чисел.

Корни четной степени извлекаются только из неотрицательных чисел. Поэтому, действуя по

Поэтому, действуя по приведенным формулам, например, с квадратными корнями,

нужно аккуратно отслеживать возможное расширение ОДЗ уравнения или неравенства и, главное, не допускать ее сужения.

Слайд 67 Решение иррационального уравнения

Решение иррационального уравнения

Слайд 68 К неравенствам вида

К неравенствам вида также

также применим метод замены множителя, вытекающий из основного правила возведения в квадрат и состоящий в следующем: множитель можно заменить множителем f-g того же знака при дополнительных условиях f, g≥0.
Важный частный случай этой замены получается в результате подстановки в ней g=0: множитель можно заменить множителем
f при f≥0.

Слайд 69 Решение иррационального неравенства

Решение иррационального неравенства

Слайд 70 ОДЗ:
Заметим, что в ОДЗ x ≥ 0, поэтому

ОДЗ:Заметим, что в ОДЗ x ≥ 0, поэтому существует и значит 

существует
и значит 

Слайд 71 Мы воспользовались здесь тем, что в ОДЗ x

Мы воспользовались здесь тем, что в ОДЗ x ≥ 0,

≥ 0,

(x – 5)(x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Кроме того, мы вынесли за скобку который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений.

Слайд 72 Имеем:
С учетом ОДЗ получаем ответ:

Имеем:С учетом ОДЗ получаем ответ:

Слайд 73 Уравнения и неравенства с модулем
Стандартное правило раскрытия модуля

Уравнения и неравенства с модулемСтандартное правило раскрытия модуля основывается на его определении:

основывается на его определении:

Слайд 74 Раскрывая сразу несколько модулей, приходится разбирать случаи, которые

Раскрывая сразу несколько модулей, приходится разбирать случаи, которые задаются знаками выражений,

задаются знаками выражений, стоящих под модулем. Однако, если количество

модулей велико, то велико и число разбираемых случаев.
Его можно заметно сократить за счет применения метода интервалов.

Слайд 75 Другой подход , напоминающий скорее не раскрытие, а

Другой подход , напоминающий скорее не раскрытие, а отбрасывание модулей, применим

отбрасывание модулей, применим к простейшим уравнениям и неравенствам вида

|f|=|g|или |f|˅g.
Он использует геометрический смысл модуля, состоящий в том, что модуль |x|численно равен расстоянию на числовой прямой от точки x до точки 0.

Слайд 76 Исходя из этого смысла, можно установить справедливость, например,

Исходя из этого смысла, можно установить справедливость, например, таких утверждений:уравнение |f|=|g|

таких утверждений:
уравнение |f|=|g| равносильно совокупности f=±g;
уравнение |f|=g равносильно системе

f=±g; g≥0;
неравенство |f|неравенство |f|>g равносильно совокупности f>g; f<-g.

Слайд 77 Полезную роль при преобразовании выражений могут сыграть следующие

Полезную роль при преобразовании выражений могут сыграть следующие свойства модулей:

свойства модулей:

Слайд 78 К неравенствам вида (|f|-|g|)xh˅0 также применим метод замены

К неравенствам вида (|f|-|g|)xh˅0 также применим метод замены множителя: множитель |f|-|g|

множителя: множитель |f|-|g| можно заменить множителем f2-g2 того же

знака.

Слайд 79 Решение уравнения с модулем
│x - 1│- 2 │x

Решение уравнения с модулем│x - 1│- 2 │x + 2│= 0

+ 2│= 0

Слайд 80 Найдем точки перемены знака модуля из условий:

Найдем точки перемены знака модуля из условий: х –

х – 1 = 0

и х + 2 = 0
х = 1 х = - 2

Рассмотрим данное уравнение на промежутках
(- ∞;-2], [-2;1] , [1;+∞)

Слайд 81 На промежутке (- ∞; -2 ] уравнение имеет

На промежутке (- ∞; -2 ] уравнение имеет вид:( – х

вид:
( – х + 1 ) – 2∙ (–

х – 2) = 0
– х + 1 +2х + 4 = 0
х + 5 = 0
х = – 5

- 5 принадлежит промежутку (- ∞; -2 ]

Слайд 82 На промежутке [-2;1] уравнение имеет вид:
( – х

На промежутке [-2;1] уравнение имеет вид:( – х + 1 )

+ 1 ) – 2∙ ( х + 2)

= 0
– х + 1– 2х – 4 = 0
– 3х – 3 = 0
3х = – 3
х = - 1

- 1 принадлежит промежутку [-2;1]

Слайд 83 На промежутке [1;+∞) уравнение имеет вид:
( х

На промежутке [1;+∞) уравнение имеет вид:( х – 1 ) –

– 1 ) – 2∙ ( х + 2)

= 0
х – 1 – 2х – 4 = 0
– х – 5 = 0
х = – 5

- 5 не принадлежит промежутку [1;+∞)

Ответ: х= -5, -1

Слайд 84 Решение неравенства с модулем

Решение неравенства с модулем
  • Имя файла: prezentatsiya-po-matematike-na-temu-reshenie-uravneniy-i-neravenstv-pri-podgotovke-k-ege.pptx
  • Количество просмотров: 169
  • Количество скачиваний: 0
- Предыдущая Методическая разработка - презентация на тему Применение кейс-технологий при формировании метопредметных УУД
Следующая - Презентация к уроку Свойства натуральных тканей животного происхождения

Похожие презентации

Синус, косинус, тангенс и котангенс. Синус, косинус, тангенс и котангенс. 169
Логические законы и правила преобразования логических выражений Логические законы и правила преобразования логических выражений 149
Лекции по алгебре и началам анализа 10 класс Лекции по алгебре и началам анализа 10 класс 162
Подготовка к ЕГЭ. Экстремумы функции. Подготовка к ЕГЭ. Экстремумы функции. 142
Тригонометрические функции углового аргумента Тригонометрические функции углового аргумента 165
Презентация по алгебре на тему Свойства степени с целым показателем (8 класс) Презентация по алгебре на тему Свойства степени с целым показателем (8 класс) 246
Шаблоны презентации по математике Шаблоны презентации по математике 156
Презентация к уроку алгебры на тему Функции(8 класс) Презентация к уроку алгебры на тему Функции(8 класс) 222
Рациональные уравнения (8 класс) Рациональные уравнения (8 класс) 189
Разработка урока по математике на тему Функция у=tg х Разработка урока по математике на тему Функция у=tg х 173
Радианная мера углов и дуг Радианная мера углов и дуг 167
Презентация по алгебре на тему Арифметическая и геометрическая прогрессии ( обобщение) Презентация по алгебре на тему Арифметическая и геометрическая прогрессии ( обобщение) 160
Линейное уравнение с двумя переменными Линейное уравнение с двумя переменными 158
Стандартный вид числа Стандартный вид числа 175
ВПР: оценка вычислений при решении практических задач. Часть 3 ВПР: оценка вычислений при решении практических задач. Часть 3 102
_Действительные числа_ 10 класс _Действительные числа_ 10 класс 216
Презентация к уроку алгебры 11 класс по теме Степенные функции Презентация к уроку алгебры 11 класс по теме Степенные функции 172
Презентация по теме Преобразование графиков функций Презентация по теме Преобразование графиков функций 150
Презентация к уроку алгебры в 7 классе. График функции Презентация к уроку алгебры в 7 классе. График функции 170
Презентация по алгебре на тему Туынды Презентация по алгебре на тему Туынды 180
Движение плоскости Движение плоскости 162
Фейерверк тригонометрических уравнений 10 класс Фейерверк тригонометрических уравнений 10 класс 171
Презентация по алгебре на тему Решение задач с помощью уравнений (7 класс) Презентация по алгебре на тему Решение задач с помощью уравнений (7 класс) 170
Презентация по математике Решение практико-ориентированных задач на проценты Презентация по математике Решение практико-ориентированных задач на проценты 161
Решение уравнения Решение уравнения 174
Дроби 8 класс Дроби 8 класс 183
Презентация по математике на тему Задачи на проценты Презентация по математике на тему Задачи на проценты 170
Презентация к уроку Косинус суммы и разности углов Презентация к уроку Косинус суммы и разности углов 186
Квадратичная функция 8-9 классы. Квадратичная функция 8-9 классы. 196
Презентация для 9 класса Графики квадратичной функции Презентация для 9 класса Графики квадратичной функции 146