Примеры 14) Примеры 1, 24) Примеры 1, 2, 34)
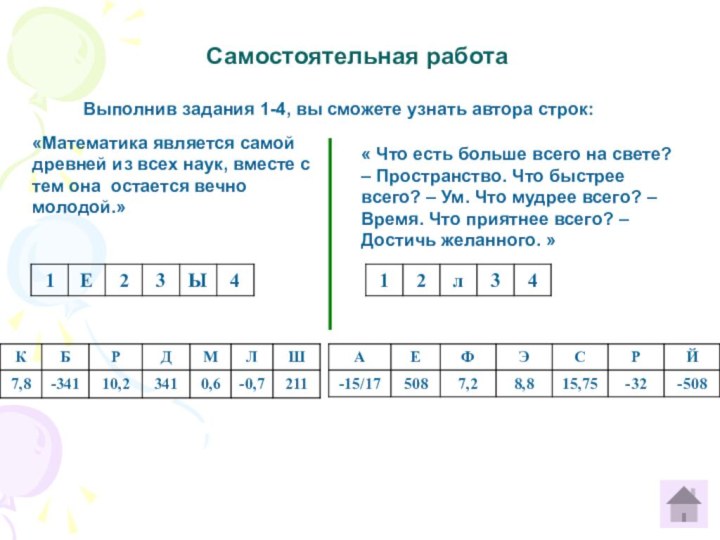
Примеры 1, 2, 3, 45)5) 5) Самостоятельная работа
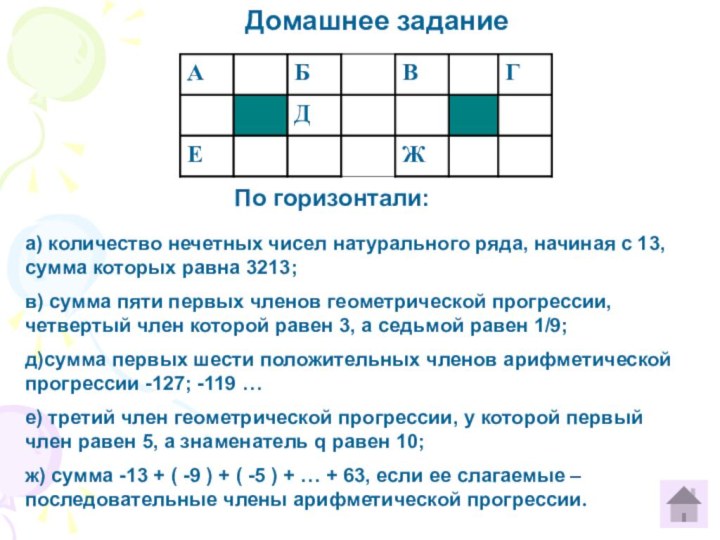
6)6) 6) Домашнее задание
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть












5)5) 5) Самостоятельная работа
6)6) 6) Домашнее задание
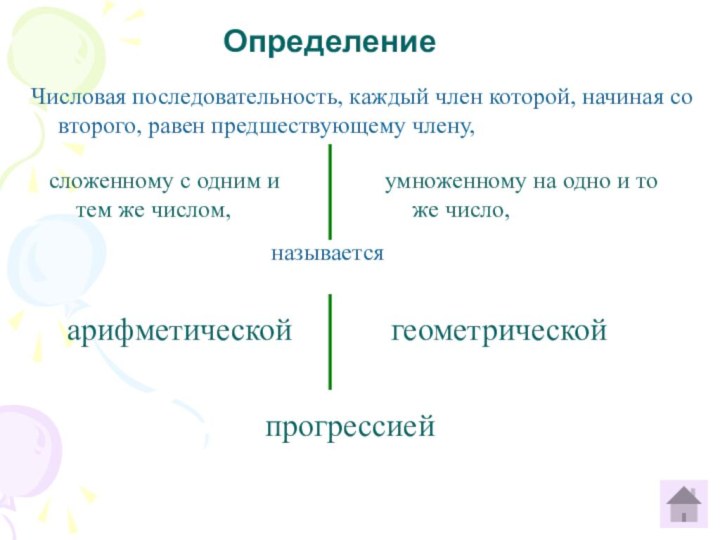
умноженному на одно и то же число,
называется
арифметической
геометрической
прогрессией
« Что есть больше всего на свете? – Пространство. Что быстрее всего? – Ум. Что мудрее всего? – Время. Что приятнее всего? – Достичь желанного. »
3) Первый член геометрической прогрессии равен 4 , а знаменатель равен 2.
Найти сумму 5 первых членов.
4) Найти сумму пяти членов геометрической прогрессии с положительными членами если:
Найти сумму семи первых членов.
4) Найти сумму шести членов геометрической прогрессии с положительными членами, если:
Найти : a4.
Найти : a3.
a1= -1,2 и d = 3.
a1 = -0,8 и d = 4.
a1 = 2, a11 = -5.
a1 = 4, a18 = -11.
b5 = 81, b3 =36.
b2 = 4, b4 =1.
Фалес (625-547 г. до н. э. ) – древнегреческий мыслитель, родоначальник античной философии и науки, основатель милетской школы.
а) количество нечетных чисел натурального ряда, начиная с 13, сумма которых равна 3213;
в) сумма пяти первых членов геометрической прогрессии, четвертый член которой равен 3, а седьмой равен 1/9;
д)сумма первых шести положительных членов арифметической прогрессии -127; -119 …
е) третий член геометрической прогрессии, у которой первый член равен 5, а знаменатель q равен 10;
ж) сумма -13 + ( -9 ) + ( -5 ) + … + 63, если ее слагаемые – последовательные члены арифметической прогрессии.
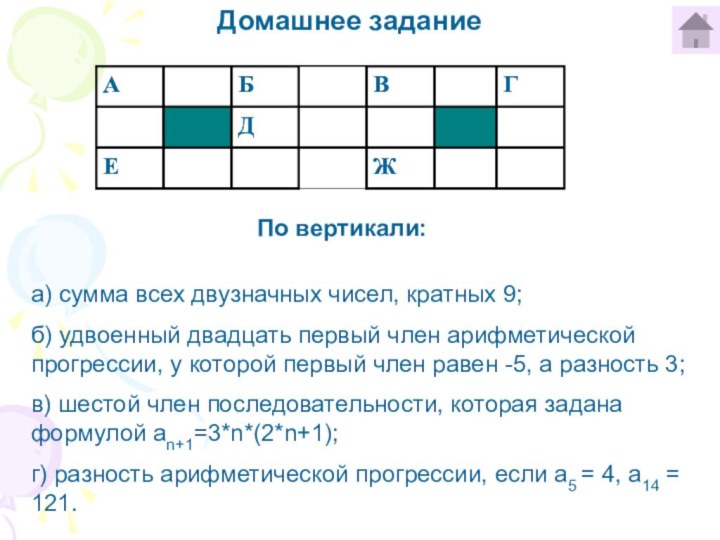
а) сумма всех двузначных чисел, кратных 9;
б) удвоенный двадцать первый член арифметической прогрессии, у которой первый член равен -5, а разность 3;
в) шестой член последовательности, которая задана формулой аn+1=3*n*(2*n+1);
г) разность арифметической прогрессии, если а5 = 4, а14 = 121.