Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике на тему Логарифмы. Свойства логарифмов.

Содержание

Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас
Тема занятия: Логарифмы. Свойства логарифмов. Десятичные и натуральные логарифмы.Лекция по дисциплине «Математика» Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас Изобретение логарифмов Уже в 1623 г., т. е. всего через 9 лет Историческая справкаТермин «ЛОГАРИФМ» предложил Дж. Непер; он возник из сочетания греческих слов Историческая справкаТермин «натуральный логарифм» принадлежит Н. Меркатору.«Характеристика» — английскому математику Г. Бригсу Портретная галереяШотландский математик, изобретатель логарифмов.Учился в Эдинбургском университете. Основными идеями учения о Рассмотрим уравнения: Определение логарифма Логарифмом положительного числа b по основанию а, где а>0, a≠0 называют Основное логарифмическое тождествоЭто равенство справедливопри b>0,a>0,a≠1. Его называют основным логарифмическим тождеством.Действие нахождения логарифма числа называют логарифмированием. Определение логарифма на языке символов: Примеры нахождения логарифмов Примеры нахождения логарифмов Задания на закреплениеРешить следующие задание по данной теме:по учебнику № 267-271. 1.2.3.Свойства, следующие из определения логарифма Взаимосвязь операции возведения в степень и логарифмирования Возведение в степеньЛогарифмирование Свойства логарифмовПусть a>0, a≠1, b>0, c>0, r – любое действительное число. 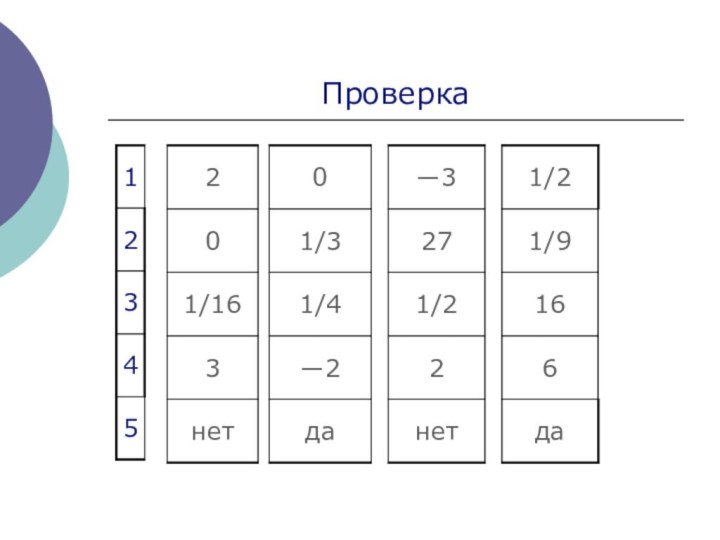Тогда справедливы формулы: Свойства логарифмов Некоторые особые обозначенияЛогарифм по основанию 10 обычно называют десятичным логарифмом и используют Устная контрольная работаНайдите логарифм следующих чисел по основанию 3: 9; 1; 1/27; Проверка Основные результатыВвели обозначение для записи корня уравнения вида Пополнили словарный запас математического Используемая литератураАлгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений/ Ш.А.
Слайды презентации

Слайд 2 Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С.

Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас

Лаплас

Слайд 3
Изобретение логарифмов
Уже в 1623 г., т. е.

Изобретение логарифмов Уже в 1623 г., т. е. всего через 9

всего через 9 лет после издания первых таблиц, английским

математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.
Вплоть до самого последнего времени, когда на наших глазах повсеместное распространение получает электронная вычислительная техника и роль логарифмов как средств вычислений резко снижается.

Слайд 4 Историческая справка
Термин «ЛОГАРИФМ» предложил Дж. Непер; он возник

Историческая справкаТермин «ЛОГАРИФМ» предложил Дж. Непер; он возник из сочетания греческих

из сочетания греческих слов logos (здесь — отношение) и

arithmos (число); в античной математике квадрат, куб и т. д. отношения а/b называются «двойным», «тройным» и т. д. отношением.

Таким образом, для Непера слова «lógu arithmós» означали «число (кратность) отношения», то есть логарифм у Дж. Непера — вспомогательное число для измерения отношения двух чисел.

Слайд 5 Историческая справка
Термин «натуральный логарифм» принадлежит Н. Меркатору.

«Характеристика» —

Историческая справкаТермин «натуральный логарифм» принадлежит Н. Меркатору.«Характеристика» — английскому математику Г.

английскому математику Г. Бригсу

«Мантисса» в нашем смысле —

логарифм – Леонарду Эйлеру

«Основание» логарифма — Леонарду Эйлеру

Понятие о модуле перехода ввёл Н. Меркатор.

Современное определение логарифма впервые дано английским математиком В. Гардинером (1742).

Знак логарифма — результат сокращения слова «ЛОГАРИФМ» — встречается в различных видах почти одновременно с появлением первых таблиц [напр., Log — у И. Кеплера (1624) и Г. Бригса (1631), log и 1. — Б. Кавальери(1632, 1643)].

Слайд 6 Портретная галерея
Шотландский математик, изобретатель логарифмов.
Учился в Эдинбургском университете.

Портретная галереяШотландский математик, изобретатель логарифмов.Учился в Эдинбургском университете. Основными идеями учения

Основными идеями учения о логарифмах Непер овладел не позднее

1594 г., однако его "Описание удивительной таблицы логарифмов", в котором изложено это учение, было издано в 1614 г.
В этом труде содержались определение логарифма, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
В "Построении удивительной таблицы логарифмов" (опубликовано в 1619) Непер изложил принцип вычисления таблиц.

Непер Джон
(1550 - 1617)

Слайд 7
Рассмотрим уравнения:



Рассмотрим уравнения:

Слайд 8 Определение логарифма
Логарифмом положительного числа b по основанию а,

Определение логарифма Логарифмом положительного числа b по основанию а, где а>0, a≠0


где а>0, a≠0
называют показатель степени, в которую нужно

возвести число а, чтобы получить число b.

Определение логарифма можно кратко записать так:






Слайд 9 Основное логарифмическое тождество
Это равенство справедливо
при b>0,a>0,a≠1.
Его называют

Основное логарифмическое тождествоЭто равенство справедливопри b>0,a>0,a≠1. Его называют основным логарифмическим тождеством.Действие нахождения логарифма числа называют логарифмированием.

основным логарифмическим тождеством.


Действие нахождения логарифма числа называют логарифмированием.

Слайд 10 Определение логарифма на языке символов:


Определение логарифма на языке символов:

Слайд 11 Примеры нахождения логарифмов

Примеры нахождения логарифмов

Слайд 12 Примеры нахождения логарифмов

Примеры нахождения логарифмов

Слайд 13 Задания на закрепление
Решить следующие задание по данной теме:
по

Задания на закреплениеРешить следующие задание по данной теме:по учебнику № 267-271.

учебнику № 267-271.

Слайд 14 1.


2.


3.

Свойства, следующие из определения логарифма






1.2.3.Свойства, следующие из определения логарифма

Слайд 15 Взаимосвязь операции возведения в степень и логарифмирования
Возведение

Взаимосвязь операции возведения в степень и логарифмирования Возведение в степеньЛогарифмирование

в степень
Логарифмирование






Слайд 16 Свойства логарифмов
Пусть a>0, a≠1, b>0, c>0, r –

Свойства логарифмовПусть a>0, a≠1, b>0, c>0, r – любое действительное число. Тогда справедливы формулы:

любое действительное число.
Тогда справедливы формулы:

Слайд 17 Свойства логарифмов

Свойства логарифмов

Слайд 18 Некоторые особые обозначения
Логарифм по основанию 10 обычно называют

Некоторые особые обозначенияЛогарифм по основанию 10 обычно называют десятичным логарифмом и

десятичным логарифмом и используют символ ,

В

математике и технике большее применение имеют логарифмы, основанием которых служит особое число е и используют символ .

Слайд 19 Устная контрольная работа
Найдите логарифм следующих чисел по основанию

Устная контрольная работаНайдите логарифм следующих чисел по основанию 3: 9; 1; 1/27;

3:
9; 1; 1/27; .
2. Найдите числа, логарифмы

которых по основанию 3, равны:
0; ―1; 3; ―2.

3. При каком основании логарифм числа 1/16 равен:
1; 2; 4; ―1?

4. Вычислите:

5. Имеет ли смысл выражение:

Слайд 20 Проверка

Проверка

Слайд 21 Основные результаты
Ввели обозначение для записи корня уравнения вида

Основные результатыВвели обозначение для записи корня уравнения вида Пополнили словарный запас


Пополнили словарный запас математического языка:
логарифм числа, основание логарифма;
десятичный логарифм,

натуральный логарифм.
Ввели новые обозначения:
Научились вычислять значения логарифма.
  • Имя файла: prezentatsiya-po-matematike-na-temu-logarifmy-svoystva-logarifmov.pptx
  • Количество просмотров: 161
  • Количество скачиваний: 0
- Предыдущая Презентация: Тест по геометрии
Следующая - Taqdimot.,,Suv eng yaxshi erituvchi

Похожие презентации

Формулы суммы синусов и косинусов двух аргументов Формулы суммы синусов и косинусов двух аргументов 169
Конференция по истории математики на тему Математика переменных величин Конференция по истории математики на тему Математика переменных величин 220
Сокращение дробей Сокращение дробей 170
Презентация по алгебре на тему Способы решения тригонометрических уравнений (10 класс) Презентация по алгебре на тему Способы решения тригонометрических уравнений (10 класс) 141
Интеграл и его применение Интеграл и его применение 162
Презентация по математике для 8 класса Понятие алгебраической дроби и ее значение Презентация по математике для 8 класса Понятие алгебраической дроби и ее значение 153
Множества Множества 176
Презентация к уроку Линейная функция, спрос и предложение Презентация к уроку Линейная функция, спрос и предложение 175
Магия чисел Магия чисел 148
Презентация по математике на тему Решение системы линейных уравнений Презентация по математике на тему Решение системы линейных уравнений 157
Презентация по математике Свойства степени с натуральным показателем. Путешествие к замку Камелота Презентация по математике Свойства степени с натуральным показателем. Путешествие к замку Камелота 165
Функции Функции 213
Показательная функция, решение уравнений и неравенств Показательная функция, решение уравнений и неравенств 166
Подготовка к ОГЭ - 9 по математике . Подготовка к ОГЭ - 9 по математике . 165
Уравнения по алгебре Уравнения по алгебре 145
Презентация по алгебре Способы решения систем уравнений (7 класс) Презентация по алгебре Способы решения систем уравнений (7 класс) 164
Графический способ решения неравенств Графический способ решения неравенств 166
просто просто 192
Задачи на дроби Задачи на дроби 144
Формулы сокращенного умножения Формулы сокращенного умножения 158
Презентация по математике на тему: Вспомни Всё Презентация по математике на тему: Вспомни Всё 141
Презентация к урокупо подготовке к ОГЭ Презентация к урокупо подготовке к ОГЭ 216
Презентация по теме: Движение Презентация по теме: Движение 157
Презентация по алгебре 9 класс на тему Формула суммы п - первых членов арифметической прогрессии Презентация по алгебре 9 класс на тему Формула суммы п - первых членов арифметической прогрессии 186
Интеграция как путь повышения качества обучения Интеграция как путь повышения качества обучения 167
Презентация к уроку по теме Равносильные уравнения Презентация к уроку по теме Равносильные уравнения 159
Презентация к уроку Свойства арифметического квадратного корня (8 класс) Презентация к уроку Свойства арифметического квадратного корня (8 класс) 293
Некоторые способы умножения многочленов одной переменной Некоторые способы умножения многочленов одной переменной 151
Презентация по алгебре на тему Формулы сокращенного умножения(7 класс) Презентация по алгебре на тему Формулы сокращенного умножения(7 класс) 171
Презентация Математическая викторина для 6-7 классов Презентация Математическая викторина для 6-7 классов 193