Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему к уроку по алгебре для 7 класса по теме Системы линейных уравнений с двумя переменными

Содержание

2. ЗАДАЧИ УРОКА: образовательные: -повторить понятие системы
3. БЛИЦ ОПРОС : Определение линейного уравнения с
4. МИНИ – ТЕСТ 1. Из предложенных
5. КЛЮЧ К ТЕСТУ 1 - б2 - а3 - в4 - в
6. Для уравнения вида ах + b у
7. Для уравнения вида ах + b у
8. ТРИ ВОЗМОЖНЫХ СЛУЧАЯ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ
9. ОПРЕДЕЛИТЕ, СКОЛЬКО РЕШЕНИЙ ИМЕЕТ СИСТЕМА УРАВНЕНИЙ.
10. ЗАКОНЧИТЕ ПРЕДЛОЖЕНИЕ, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ УТВЕРЖДЕНИЕВариант
11. ЗАДАНИЕ. В КАЖДОМ ЗАДАНИИ ИЗ ТРЕХ ПРЕДЛОЖЕННЫХ
12. ЗАДАНИЕ . ПОКАЗАТЬ, ЧТО СИСТЕМА УРАВНЕНИЙ ИМЕЕТ
13. ПОДБЕРИТЕ ТАКОЕ ЗНАЧЕНИЕ K, ПРИ КОТОРОМ
14. ГРАФИЧЕСКИЙ СПОСОБ (АЛГОРИТМ)Выразить у через х в
15. РЕШЕНИЕ СИСТЕМЫ ГРАФИЧЕСКИМ СПОСОБОМy=10 - xy=x+2Выразим учерез хПостроим графикпервого уравненияу=х+2Построим графиквторого уравненияу=10 - хОтвет: (4; 6)
16. ЗАРЯДКА ДЛЯ ГЛАЗ
17. СПОСОБ ПОДСТАНОВКИ (АЛГОРИТМ)Из какого-либо уравнения выразить одну
18. РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ ПОДСТАНОВКИ7х - 2х - 4 = 1;5х = 5;х=1;Ответ: х=1; у=6.
19. РЕШИТЬ СИСТЕМУ МЕТОДОМ ПОДСТАНОВКИ1 вариант х
20. РЕШЕНИЕ СИСТЕМЫ 1 ВАРИАНТА х +
21. РЕШЕНИЕ СИСТЕМЫ 2 ВАРИАНТА 3(х+2у)+5(3х-у)=75 2х –
22. Выразить у через х (или х через
23. РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ СРАВНЕНИЯПриравняемвыражениядля у7х - 1=2х+4,7х - 2х=4+1,5х=5,х=1.РешимуравнениеОтвет: (1; 6)
24. СПОСОБ СЛОЖЕНИЯ (АЛГОРИТМ)Уравнять модули коэффициентов при какой-нибудь
25. РЕШИТЕ СИСТЕМЫ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ 1 .
26. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙВариант 1Вариант 2Тест.2х -
27. ВЫВОД: Итак, одну и ту же
28. ИСААК НЬЮТОН СКАЗАЛ: «Чтобы решить вопрос, относящийся
29. С ПОМОЩЬЮ КАКОЙ ИЗ СИСТЕМ, МОЖНО РЕШИТЬ
30. СХЕМА РЕШЕНИЯ ЗАДАЧИ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ:1).
32. СОСТАВЬТЕ СИСТЕМУ УРАВНЕНИЙ ПО УСЛОВИЮ ЗАДАЧИ:« Одна
33. ОПИШИТЕ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ СИТУАЦИЮРазность двух
34. РЕШИТЬ ЗАДАЧУ:Миша купил 2 чупа-чупса и 1
35. ЗАДАЧА: В гостинице 25 номеров.
36. РЕШЕНИЕ:Пусть х номеров 4-х местных, а у - 2-х местных. Составим и решим систему:
37. ЗАДАЧАВ кассе лежит 480 рублей монетами достоинством
38. Решение:Пусть в кассе х (шт.) монет по
39. КОНТРОЛЬНАЯ РАБОТА ТЕМА: «СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ»
40. 1. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ.
41. Скачать презентацию
42. Похожие презентации

ЗАДАЧИ УРОКА: образовательные: -повторить понятие системы линейных уравнений с двумя переменными, ее решения, графический метод, метод подстановки; - отработать графический способ решения системы линейных уравнений, рассмотреть применение систем как модели реальных ситуаций;- закрепить навыки построения графиков

Главная
Алгебра
Презентация к уроку по алгебре для 7 класса по теме Системы линейных уравнений с двумя переменными

ЗАДАЧИ УРОКА: образовательные: -повторить понятие системы линейных уравнений с двумя переменными,

БЛИЦ ОПРОС : Определение линейного уравнения с двумя переменными.Что является решением линейного

МИНИ – ТЕСТ 1. Из предложенных уравнений выберите линейное с двумя

Для уравнения вида ах + b у = с найти значения

ТРИ ВОЗМОЖНЫХ СЛУЧАЯ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ – ГРАФИКОВ УРАВНЕНИЙ СИСТЕМЫПрямыепараллельныПрямые пересекаютсяПрямые

ОПРЕДЕЛИТЕ, СКОЛЬКО РЕШЕНИЙ ИМЕЕТ СИСТЕМА УРАВНЕНИЙ.

ЗАКОНЧИТЕ ПРЕДЛОЖЕНИЕ, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ УТВЕРЖДЕНИЕВариант 1.А). Если графики двух линейных

ЗАДАНИЕ. В КАЖДОМ ЗАДАНИИ ИЗ ТРЕХ ПРЕДЛОЖЕННЫХ ОТВЕТОВ ВЫБЕРИТЕ ВЕРНЫЙВариант 1.1) Укажите

ЗАДАНИЕ . ПОКАЗАТЬ, ЧТО СИСТЕМА УРАВНЕНИЙ ИМЕЕТ БЕСКОНЕЧНО МНОГО РЕШЕНИЙ. ЧТО ЭТО

ПОДБЕРИТЕ ТАКОЕ ЗНАЧЕНИЕ K, ПРИ КОТОРОМ СИСТЕМА Имеет единственное решение

ГРАФИЧЕСКИЙ СПОСОБ (АЛГОРИТМ)Выразить у через х в каждом уравненииПостроить в одной системе

РЕШЕНИЕ СИСТЕМЫ ГРАФИЧЕСКИМ СПОСОБОМy=10 - xy=x+2Выразим учерез хПостроим графикпервого уравненияу=х+2Построим графиквторого уравненияу=10 - хОтвет: (4; 6)

СПОСОБ ПОДСТАНОВКИ (АЛГОРИТМ)Из какого-либо уравнения выразить одну переменную через другуюПодставить полученное выражение

РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ ПОДСТАНОВКИ7х - 2х - 4 = 1;5х = 5;х=1;Ответ: х=1; у=6.

РЕШИТЬ СИСТЕМУ МЕТОДОМ ПОДСТАНОВКИ1 вариант х + у = 7

РЕШЕНИЕ СИСТЕМЫ 2 ВАРИАНТА 3(х+2у)+5(3х-у)=75 2х – 3у =-118х+у =75 2х –

Выразить у через х (или х через у) в каждом уравненииПриравнять выражения,

РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ СРАВНЕНИЯПриравняемвыражениядля у7х - 1=2х+4,7х - 2х=4+1,5х=5,х=1.РешимуравнениеОтвет: (1; 6)

СПОСОБ СЛОЖЕНИЯ (АЛГОРИТМ)Уравнять модули коэффициентов при какой-нибудь переменнойСложить почленно уравнения системыСоставить новую

РЕШИТЕ СИСТЕМЫ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ 1 . 5х-2у=6,

РЕШИТЕ СИСТЕМУ УРАВНЕНИЙВариант 1Вариант 2Тест.2х - у = 1,Х + у

ВЫВОД: Итак, одну и ту же систему можно решить разными способами.

ИСААК НЬЮТОН СКАЗАЛ: «Чтобы решить вопрос, относящийся к числам или к отвлеченным

С ПОМОЩЬЮ КАКОЙ ИЗ СИСТЕМ, МОЖНО РЕШИТЬ СЛЕДУЮЩУЮ ЗАДАЧУСумма двух чисел равна

СХЕМА РЕШЕНИЯ ЗАДАЧИ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ:1). вводят обозначения неизвестных и

СОСТАВЬТЕ СИСТЕМУ УРАВНЕНИЙ ПО УСЛОВИЮ ЗАДАЧИ:« Одна сторона прямоугольника меньше другой на

ОПИШИТЕ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ СИТУАЦИЮРазность двух чисел равна 12. Одно из

РЕШИТЬ ЗАДАЧУ:Миша купил 2 чупа-чупса и 1 жевачку и заплатил 5 руб.

ЗАДАЧА: В гостинице 25 номеров. Есть 4-х местные и 2-х

РЕШЕНИЕ:Пусть х номеров 4-х местных, а у - 2-х местных. Составим и решим систему:

ЗАДАЧАВ кассе лежит 480 рублей монетами достоинством по 2 рубля и по

Решение:Пусть в кассе х (шт.) монет по 5 р., у (шт) монет

КОНТРОЛЬНАЯ РАБОТА ТЕМА: «СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ»

1. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ. Вариант 1

Спасибо за урокДом.задание№ 11.12(а); 12.5 (а);12.24

Слайды презентации

Слайд 2 ЗАДАЧИ УРОКА:
образовательные:
-повторить понятие системы линейных уравнений

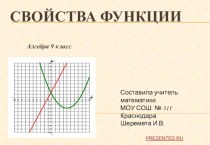
с двумя переменными, ее решения, графический метод, метод подстановки;
-

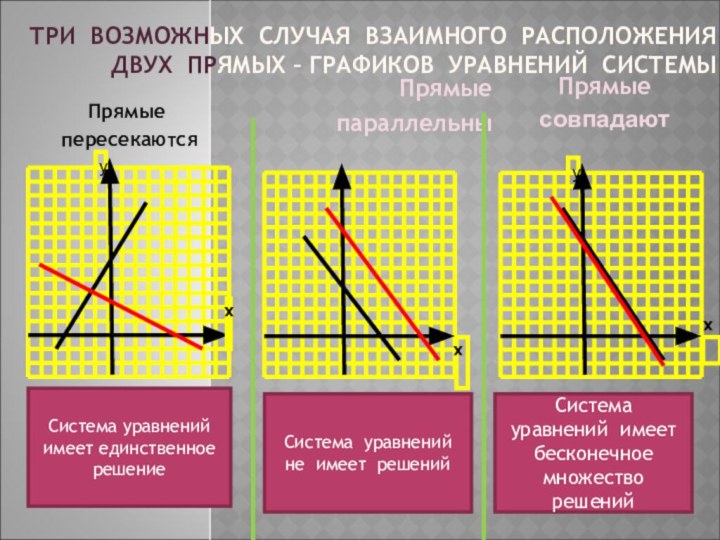
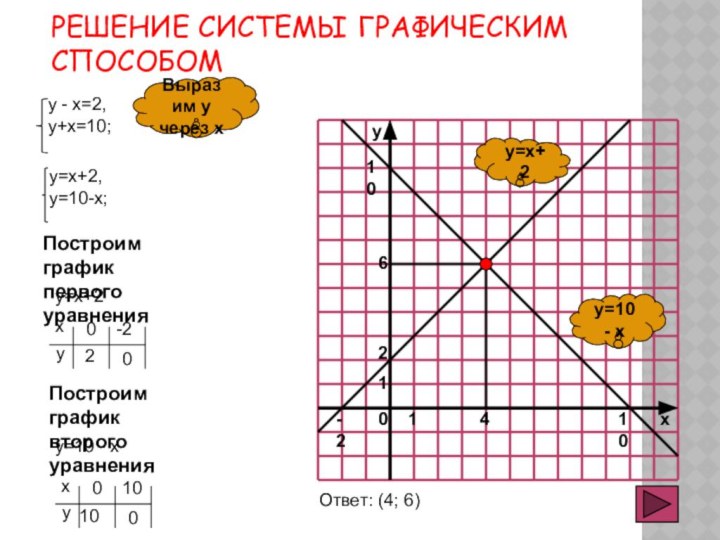
отработать графический способ решения системы линейных уравнений, рассмотреть применение систем как модели реальных ситуаций;
- закрепить навыки построения графиков линейных функций;
- формировать навыки самостоятельной работы;

развивающие:
- развивать логическое мышление, математическую речь, вычислительные навыки;
- развивать умение применять полученные знания к решению прикладных задач;
-расширение кругозора;

воспитывающие:
- воспитание познавательного интереса к предмету;
- воспитание у учащихся дисциплинированности на уроках;
- воспитание аккуратности, внимательности, рационального использования времени при выполнении заданий.

Слайд 3 БЛИЦ ОПРОС :

Определение линейного уравнения с двумя переменными.
Что

БЛИЦ ОПРОС : Определение линейного уравнения с двумя переменными.Что является решением

является решением линейного уравнения с двумя переменными?
В каком случае

говорят, что уравнения образуют систему?
Что значит решить систему?
Что является решением системы?
Сколько решений может иметь система?

Слайд 4 МИНИ – ТЕСТ
1. Из предложенных уравнений выберите

линейное с двумя переменными :
а) 3х2+ 5x

- 4 = 0; б) -2x + 4,5y - 8 = 0; в) 125x - 12 = 0

2. Какая из пар является решением уравнения 5х + 3у – 19 = 0
а) (2; 3); б) (5; 6); в) (1; 2)?
3. Сколько решений имеет уравнение
3х + 2у – 16 = 0
а) 1; б) 3; в) много?
4. Какая из пар является решением системы:
5х – 8у =31
3х + у =7

а) (4;-5) б) (2;1) в) (3;-2)

Слайд 5 КЛЮЧ К ТЕСТУ
1 - б

2 - а

3 -

в

4 - в

Слайд 6 Для уравнения вида ах + b у =

с найти значения а, b, и с и заполнить

таблицу:

Слайд 7 Для уравнения вида ах + b у =

с найти значения а, b, и с и заполнить

таблицу:

Слайд 8 ТРИ ВОЗМОЖНЫХ СЛУЧАЯ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ –

ТРИ ВОЗМОЖНЫХ СЛУЧАЯ ВЗАИМНОГО РАСПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ – ГРАФИКОВ УРАВНЕНИЙ СИСТЕМЫПрямыепараллельныПрямые

ГРАФИКОВ УРАВНЕНИЙ СИСТЕМЫ
Прямые
параллельны

Прямые
пересекаются
Прямые
совпадают
Система уравнений имеет единственное

решение

Система уравнений не имеет решений

Система уравнений имеет бесконечное множество решений

Слайд 9 ОПРЕДЕЛИТЕ, СКОЛЬКО РЕШЕНИЙ ИМЕЕТ СИСТЕМА УРАВНЕНИЙ.

Слайд 10 ЗАКОНЧИТЕ ПРЕДЛОЖЕНИЕ, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ УТВЕРЖДЕНИЕ
Вариант 1.
А). Если

ЗАКОНЧИТЕ ПРЕДЛОЖЕНИЕ, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ УТВЕРЖДЕНИЕВариант 1.А). Если графики двух

графики двух линейных уравнений системы пересекаются, то система уравнений

имеет __
единственное решение
Б). Если система двух линейных уравнений с двумя неизвестными имеет бесконечное множество решений, то графики уравнений системы _______
совпадают

Вариант 2.
А). Если графики уравнений системы линейных уравнений – параллельные прямые, то эта система ____
не имеет решения
Б). Если система двух линейных уравнений с двумя неизвестными имеет единственное решение, то графики уравнений системы ________________________
пересекаются

Слайд 11 ЗАДАНИЕ. В КАЖДОМ ЗАДАНИИ ИЗ ТРЕХ ПРЕДЛОЖЕННЫХ ОТВЕТОВ ВЫБЕРИТЕ

ЗАДАНИЕ. В КАЖДОМ ЗАДАНИИ ИЗ ТРЕХ ПРЕДЛОЖЕННЫХ ОТВЕТОВ ВЫБЕРИТЕ ВЕРНЫЙВариант 1.1)

ВЕРНЫЙ
Вариант 1.
1) Укажите взаимное расположение прямых:
2х – у

= 4 и 3х – у = 6.
А). пересекаются;
Б). совпадают;
В). параллельны.
2)Выберите систему уравнений,
соответствующую данному чертежу.

Вариант 2.
1).Укажите взаимное расположение прямых: 2х – у = 3 и х – у = 2.
А). пересекаются;
Б). совпадают;
В). параллельны.
2)Выберите систему равнений,
соответствующую данному чертежу.

Б)

В)

А)

Б)

А)

В)

Слайд 12 ЗАДАНИЕ . ПОКАЗАТЬ, ЧТО СИСТЕМА УРАВНЕНИЙ ИМЕЕТ БЕСКОНЕЧНО МНОГО РЕШЕНИЙ.

ЗАДАНИЕ . ПОКАЗАТЬ, ЧТО СИСТЕМА УРАВНЕНИЙ ИМЕЕТ БЕСКОНЕЧНО МНОГО РЕШЕНИЙ. ЧТО

ЧТО ЭТО ОЗНАЧАЕТ ГЕОМЕТРИЧЕСКИ ?
Решение.
1. Разделив обе

части первого уравнения на 2 и обе части второго уравнения на 3, получим систему …………………
2. Уравнения системы оказались ………… это означает, что система ……. Геометрически это означает, что графиками этих уравнений являются………….

Слайд 13 ПОДБЕРИТЕ ТАКОЕ ЗНАЧЕНИЕ K, ПРИ КОТОРОМ СИСТЕМА
Имеет

единственное решение

у= 3х – 5

у= kх + 4

Не имеет решений

у =5х – 7
у =kх - 7

Слайд 14 ГРАФИЧЕСКИЙ СПОСОБ (АЛГОРИТМ)
Выразить у через х в каждом

ГРАФИЧЕСКИЙ СПОСОБ (АЛГОРИТМ)Выразить у через х в каждом уравненииПостроить в одной

уравнении
Построить в одной системе координат график каждого уравнения
Определить координаты

точки пересечения
Записать ответ: х=…; у=… , или (х; у)

Слайд 15 РЕШЕНИЕ СИСТЕМЫ ГРАФИЧЕСКИМ СПОСОБОМ

y=10 - x
y=x+2
Выразим у
через х
Построим

график
первого уравнения
у=х+2
Построим график
второго уравнения
у=10 - х
Ответ: (4; 6)

Слайд 16 ЗАРЯДКА ДЛЯ ГЛАЗ

Слайд 17 СПОСОБ ПОДСТАНОВКИ (АЛГОРИТМ)
Из какого-либо уравнения выразить одну переменную

СПОСОБ ПОДСТАНОВКИ (АЛГОРИТМ)Из какого-либо уравнения выразить одну переменную через другуюПодставить полученное

через другую
Подставить полученное выражение для переменной в другое уравнение

и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .

Слайд 18 РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ ПОДСТАНОВКИ
7х - 2х - 4

= 1;
5х = 5;
х=1;
Ответ: х=1; у=6.

Слайд 19 РЕШИТЬ СИСТЕМУ МЕТОДОМ ПОДСТАНОВКИ
1 вариант

х +

у = 7
2х + у = 8
2

вариант

Слайд 20 РЕШЕНИЕ СИСТЕМЫ 1 ВАРИАНТА
х + у

= 7
2х + у = 8

Решим второе

уравнение:
14 - 2у + у = 8
-у = 8-14
-у = -6
у = 6

х= 7 - у
2(7-у) + у = 8

у = 6
х = 7-у
у = 6
х = 7-6
у = 6
х = 1 Ответ:(1;6)

Слайд 21 РЕШЕНИЕ СИСТЕМЫ 2 ВАРИАНТА

3(х+2у)+5(3х-у)=75
2х – 3у

=-1

18х+у =75
2х – 3у =-1

2х-225+54х=-1
56х=224
х=4

3х+6у+15х-5у=75
2х – 3у =-1

у=75-18х
2х-3(75-18х)=-1

х=4
у=3 Ответ:(4;3)

Слайд 22
Выразить у через х (или х через у)

Выразить у через х (или х через у) в каждом уравненииПриравнять

в каждом уравнении
Приравнять выражения, полученные для одноимённых переменных
Решить полученное

уравнение и найти значение одной переменной
Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
Записать ответ: ( Х; У ).

Способ сравнения ( алгоритм )

Слайд 23 РЕШЕНИЕ СИСТЕМЫ СПОСОБОМ СРАВНЕНИЯ
Приравняем
выражения
для у
7х - 1=2х+4,
7х -

2х=4+1,
5х=5,
х=1.
Решим
уравнение
Ответ: (1; 6)

Слайд 24 СПОСОБ СЛОЖЕНИЯ (АЛГОРИТМ)

Уравнять модули коэффициентов при какой-нибудь переменной
Сложить

СПОСОБ СЛОЖЕНИЯ (АЛГОРИТМ)Уравнять модули коэффициентов при какой-нибудь переменнойСложить почленно уравнения системыСоставить

почленно уравнения системы
Составить новую систему: одно уравнение новое, другое

- одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .

Слайд 25 РЕШИТЕ СИСТЕМЫ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ
1 .

5х-2у=6,
7х+2у=-6;

2.

3.

1.
Ответ: ( 1; - 0,5 )

2.
Ответ: ( -1; 6 ).

3.
Ответ: ( -12; 10 ).

х + 3у= 17,
2у – х = 13;

5 х + 6у= 0,
3х + 4у = 4;

Слайд 26 РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ

Вариант 1

Вариант 2
Тест.
2х - у

РЕШИТЕ СИСТЕМУ УРАВНЕНИЙВариант 1Вариант 2Тест.2х - у = 1,Х +

= 1,
Х + у = - 4,

3х + у

= -1,
Х - у = 5,

и, обозначив ( m ; n ) решение системы, вычислите значение выражения : m² + n² .

а). 17; б). 5;
в). 13; г). 10.

а). 25; б). 17;
в). 10; г). 5.

Слайд 27 ВЫВОД:
Итак, одну и ту же систему

можно решить разными способами.
Какой из них вам

показался более удобным?
В чем недостаток каждого метода?

Слайд 28 ИСААК НЬЮТОН СКАЗАЛ:
«Чтобы решить вопрос, относящийся к

ИСААК НЬЮТОН СКАЗАЛ: «Чтобы решить вопрос, относящийся к числам или к

числам или к отвлеченным отношениям величин, нужно лишь перевести

задачу с родного языка на алгебраический.»

Слайд 29 С ПОМОЩЬЮ КАКОЙ ИЗ СИСТЕМ, МОЖНО РЕШИТЬ СЛЕДУЮЩУЮ

С ПОМОЩЬЮ КАКОЙ ИЗ СИСТЕМ, МОЖНО РЕШИТЬ СЛЕДУЮЩУЮ ЗАДАЧУСумма двух чисел

ЗАДАЧУ
Сумма двух чисел равна 7, а их разность 3.Найти

эти числа.

1) х-у=7
х+у=3

2) х+у=7
ху=3

3) х+у=7
Х-у=3

Слайд 30 СХЕМА РЕШЕНИЯ ЗАДАЧИ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ:
1). вводят

обозначения неизвестных и

составляют систему уравнений;
2). решают систему уравнений;
3). Возвращаясь к условию задачи и
использованным обозначениям,
записывают ответ.

Слайд 31 УСТНЫЕ УПРАЖНЕНИЯ
Составьте систему уравнений по условию

задачи:
«На двух полках 60 книг. На второй полке на

10 книг меньше, чем на первой. Сколько книг на каждой полке ?»

Слайд 32 СОСТАВЬТЕ СИСТЕМУ УРАВНЕНИЙ ПО УСЛОВИЮ ЗАДАЧИ:
« Одна сторона

СОСТАВЬТЕ СИСТЕМУ УРАВНЕНИЙ ПО УСЛОВИЮ ЗАДАЧИ:« Одна сторона прямоугольника меньше другой

прямоугольника меньше другой на 5 см, периметр прямоугольника равен

38 см. Найти стороны этого прямоугольника.»
ВЫБЕРИТЕ ПРАВИЛЬНЫЙ ОТВЕТ.

А) Х – У = 5, Б) Х + У = 5, В) Х – У = 5
Х + У = 38; 2(Х + У) = 38; 2(Х + У) = 38;

Слайд 33 ОПИШИТЕ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ СИТУАЦИЮ
Разность двух чисел

ОПИШИТЕ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ СИТУАЦИЮРазность двух чисел равна 12. Одно

равна 12. Одно из них больше другого в 4

раза.

х – у = 12
х = 4у

В классе 36 учеников. Девочек на 3 меньше, чем мальчиков.

х + у = 36
х – у = 3

Слайд 34 РЕШИТЬ ЗАДАЧУ:
Миша купил 2 чупа-чупса и 1 жевачку

РЕШИТЬ ЗАДАЧУ:Миша купил 2 чупа-чупса и 1 жевачку и заплатил 5

и заплатил 5 руб. Если бы он купил 8

чупа-чупсов, то на 12 руб заплатил больше чем при покупке 4 жевачек. Сколько стоит 1 чупа-чупс и 1 жевачка.

8х-4у=12
2х+у=5

Слайд 35 ЗАДАЧА:
В гостинице 25 номеров. Есть 4-х

местные и 2-х местные номера. Сколько каких номеров, если

известно, что всего в гостинице могут разместиться 70 человек?

Слайд 36 РЕШЕНИЕ:
Пусть х номеров 4-х местных, а у -

2-х местных. Составим и решим систему:

Слайд 37 ЗАДАЧА
В кассе лежит 480 рублей монетами достоинством по

ЗАДАЧАВ кассе лежит 480 рублей монетами достоинством по 2 рубля и

2 рубля и по 5 рублей. Сколько 2-х рублёвых

и 5-ти рублёвых монет в кассе, если всего 120 монет.

Слайд 38
Решение:
Пусть в кассе х (шт.) монет по 5

Решение:Пусть в кассе х (шт.) монет по 5 р., у (шт)

р., у (шт) монет по 2 р.

х= 80 монет

по 5 р.
у= 40 монет по 2 р.

Слайд 39 КОНТРОЛЬНАЯ РАБОТА ТЕМА: «СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ»

Слайд 40 1. РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ СПОСОБОМ СЛОЖЕНИЯ.

Вариант 1

Вариант 2

х – у = - 1,
2х + у = 4.

х + у = 3,
2х - у = 3.

2. Решите систему уравнений способом подстановки.

2 х + у = 2,
4х -3 у = 24.

3х +2 у = 6,
2х - у = 1.

3. Решите задачу.

Двое рабочих изготовили вместе 237 детали, первый рабочий работал 8 дней, второй – 5. Сколько деталей изготовил каждый рабочий за один день, если первый изготавливал на 2 детали в день больше, чем второй ?.

На покупку трех тренировочных костюмов и пяти мячей было потрачено 255 $.Сколько стоит один костюм и один мяч, если стоимость четырех мячей такая же, как стоимость одного костюма?