Презентация на тему по математике Коэффициент наклона прямой, 10 класс

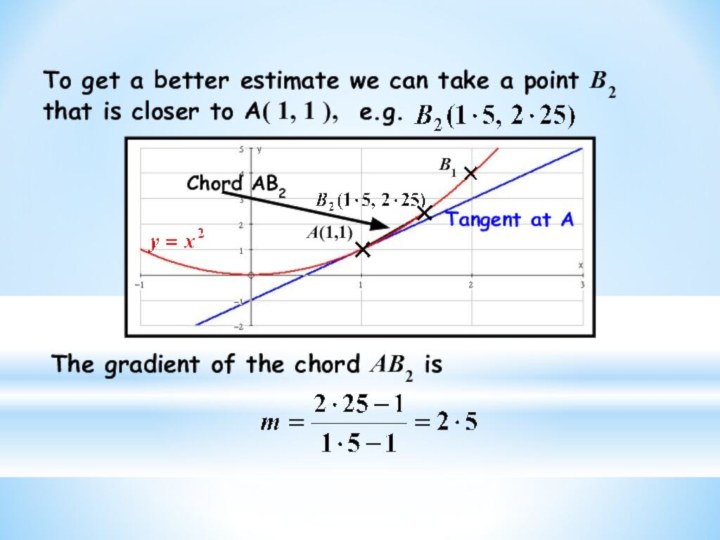
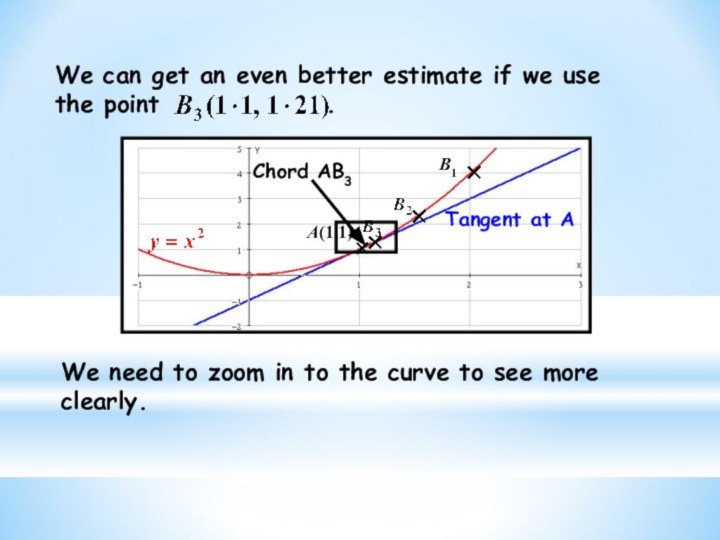
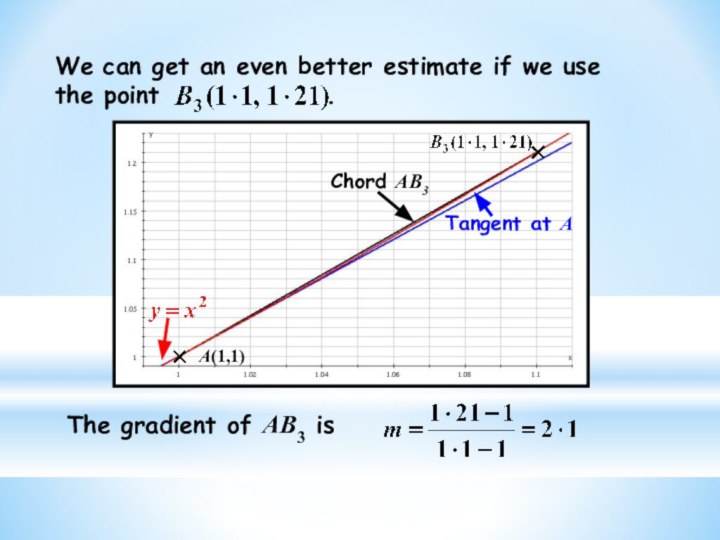
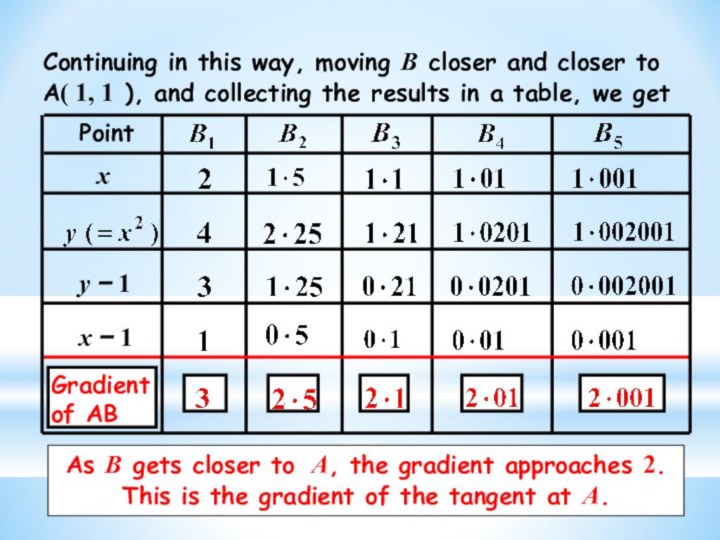
a pattern in results found by measuring gradients of

However, if we want to prove the rule or find a rule for some other functions we need a method based on algebra.

This presentation shows you how this is done.

The emphasis in this presentation is upon understanding ideas rather than doing calculations.

point ( 2, 4 ).
( We are going to

As an approximation to the gradient of the tangent we can use the gradient of a chord from A to a point close to A.

by
B1
A(1,1)
(2,4)
Tangent at A
We can see

Chord AB1

to see more clearly.

closer to A( 1, 1 ), and collecting the

As B gets closer to A, the gradient approaches 2. This is the gradient of the tangent at A.

of the chord AB approaches the gradient of the

of B that suggests it is near to A.

m where

gradient of the curve, so