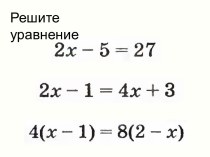с понятием целого рационального;
с понятием степени уравнения;
формируем навыки решения
уравнений;контролируем уровень усвоения материала;
На уроке можем ошибаться, сомневаться, консультироваться.
Каждый учащийся сам себе дает установку.