числа а (n = 2, 3, 4, 5, ...)
называют такое неотрицательное число, при возведении которого в степень п получается число а.Число а называют подкоренным числом,
а число n – показателем корня
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











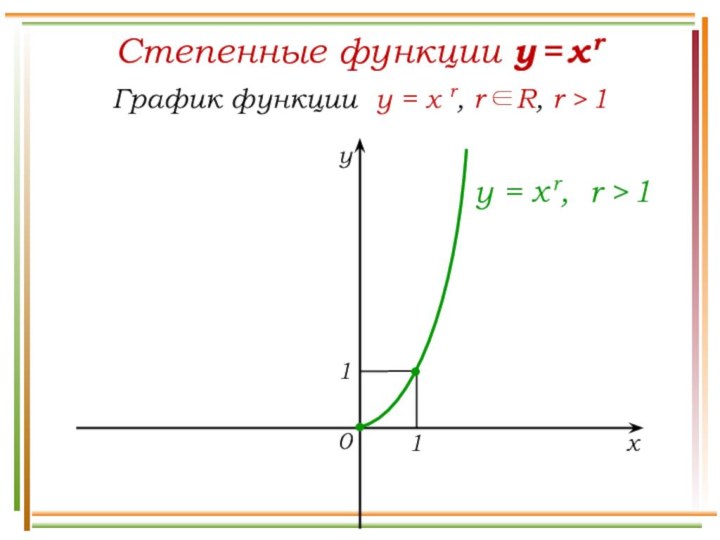

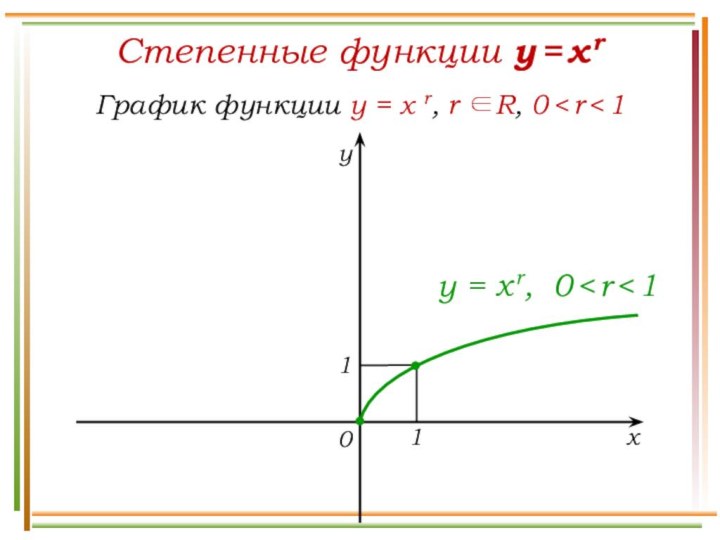

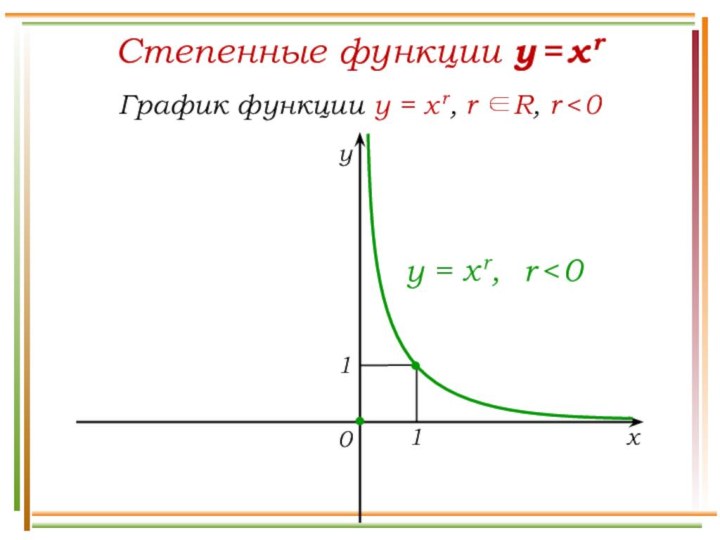
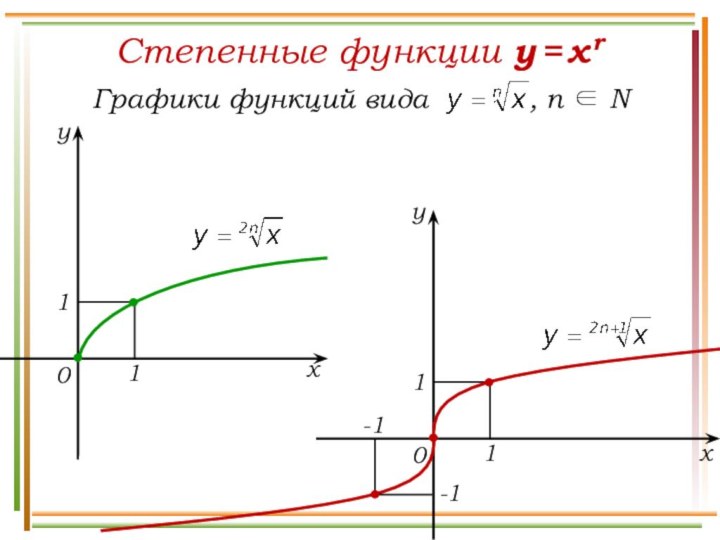





Число а называют подкоренным числом,
а число n – показателем корня