Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по алгебре на тему: Область определения и множество значений тригонометических функций (11 класс)

Содержание

Знания и навыки учащихсяЗнать определение области определения и множества значений функции, в том числе тригонометрических функцийУметь находить область определения и область значений тригонометрических функций
Область определения и множество значений тригонометрических функцийУрок 1 Знания и навыки учащихсяЗнать определение области определения и множества значений функции, в ПовторениеПусть есть два множества Х и У. Если каждому элементу х из ПовторениеВсе значения независимой переменной образуют область определения функциихy=f(x)fОбласть определения функциимножество значений функцииВсе ПовторениеИтак, если M(t) = M(x;y)тогда x = cos t Новый материалФункции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями.y = Новый материалRRRR Решение упражненийУстно: Найдите область определения функции:1) 2)3) 4)5) Решение упражненийУстно: Найдите множество значений функции:1) 2)3) 4) Решение упражненийПисьменно: Найти множество значений функции:1)2) Решение упражнений Найдите область определения функции:1)2) ° 00π Решение упражнений Найдите область определения функции:3) Решение упражненийНайдите область определения функции:4) УчебникСтр. 6-7№ 3 (1,3)№ 4 (1)№ 6 (1,3)№ 7 (1,3,5)№ 8 (1,3) Домашнее задание стр. 3 пар. 1№ 3 – 5 (четн)№ 7 (четн)
Слайды презентации

Слайд 2 Знания и навыки учащихся
Знать определение области определения и

Знания и навыки учащихсяЗнать определение области определения и множества значений функции,

множества значений функции, в том числе тригонометрических функций
Уметь находить

область определения и область значений тригонометрических функций

Слайд 3 Повторение
Пусть есть два множества Х и У.
Если

ПовторениеПусть есть два множества Х и У. Если каждому элементу х

каждому элементу х из множества Х по некоторому правилу

сопоставлен вполне определенный элемент у из множества У, то говорят, что задана функция
и пишут у=f(x), где
х – независимой переменной (аргументом),
у – зависимой переменной (функцией).

Слайд 4

Повторение
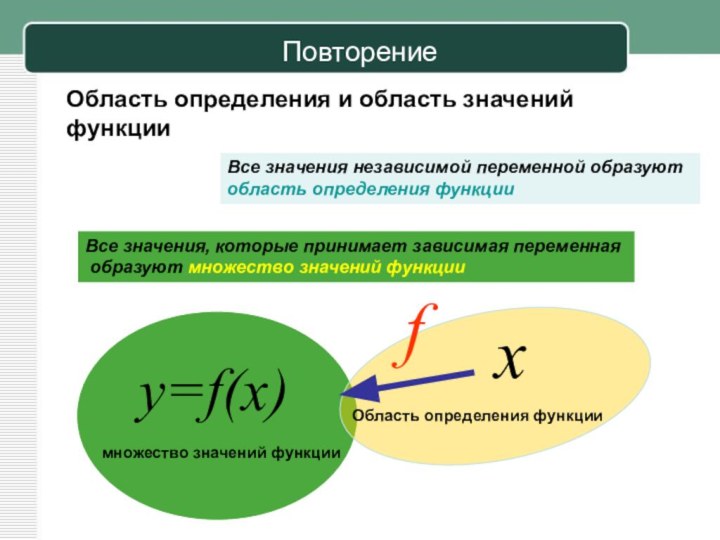
Все значения независимой переменной образуют
область определения функции
х
y=f(x)
f
Область

ПовторениеВсе значения независимой переменной образуют область определения функциихy=f(x)fОбласть определения функциимножество значений

определения функции
множество значений функции
Все значения, которые принимает зависимая переменная

образуют множество значений функции

Область определения и область значений функции

Слайд 5 Повторение
Итак, если
M(t) = M(x;y)
тогда
x

ПовторениеИтак, если M(t) = M(x;y)тогда x = cos t y

= cos t
y = sin t

Если

точка M числовой окружности соответствует числу t, то
абсциссу точки M называют косинусом числа t и обозначают cos t,
а ординату точки M называют синусом числа t и обозначают sin t.

Слайд 6 Новый материал
Функции синус, косинус, тангенс и котангенс называют

Новый материалФункции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями.y

основными тригонометрическими функциями.

y = sin x;

y = cos x;
y = tg x; y = ctg x;

Слайд 7 Новый материал
R
R
R
R

Новый материалRRRR

Слайд 8 Решение упражнений
Устно: Найдите область определения функции:
1)
2)

3)

Решение упражненийУстно: Найдите область определения функции:1) 2)3) 4)5)




4)

5)

Слайд 9 Решение упражнений
Устно: Найдите множество значений функции:
1)
2)

3)

Решение упражненийУстно: Найдите множество значений функции:1) 2)3) 4)



4)

Слайд 10 Решение упражнений
Письменно: Найти множество значений функции:

1)

2)

Решение упражненийПисьменно: Найти множество значений функции:1)2)

Слайд 11 Решение упражнений
Найдите область определения функции:
1)

2)

°
0
0
π

Решение упражнений Найдите область определения функции:1)2) ° 00π

Слайд 12 Решение упражнений
Найдите область определения функции:
3)



Решение упражнений Найдите область определения функции:3)

Слайд 13 Решение упражнений
Найдите область определения функции:

4)

Решение упражненийНайдите область определения функции:4)

Слайд 14 Учебник
Стр. 6-7
№ 3 (1,3)
№ 4 (1)
№ 6 (1,3)
№

УчебникСтр. 6-7№ 3 (1,3)№ 4 (1)№ 6 (1,3)№ 7 (1,3,5)№ 8 (1,3)

7 (1,3,5)
№ 8 (1,3)

  • Имя файла: prezentatsiya-po-algebre-na-temu-oblast-opredeleniya-i-mnozhestvo-znacheniy-trigonometicheskih-funktsiy-11-klass.pptx
  • Количество просмотров: 592
  • Количество скачиваний: 171
- Предыдущая Развитие речи детей дошкольного возраста средствами малых форм фольклора с учетом введения ФГОС ДО
Следующая - Презентация по английскому языку на тему:Слова-действия

Похожие презентации

Диктант по алгебре и началам математического анализа по теме Показательная функция Диктант по алгебре и началам математического анализа по теме Показательная функция 179
Презентация к уроку на тему Определение степени с целым отрицательным показателем (8 класс) Презентация к уроку на тему Определение степени с целым отрицательным показателем (8 класс) 266
Производная и ее геометрический смысл Производная и ее геометрический смысл 163
Линейные неравенства с параметром Линейные неравенства с параметром 159
Графики Графики 217
Стандартный вид числа Стандартный вид числа 207
Презентация по алгебре вынисение общего множителя Презентация по алгебре вынисение общего множителя 164
Методы решения логарифмических уравнений Методы решения логарифмических уравнений 165
Задачи с практическим содержанием (7 класс) Задачи с практическим содержанием (7 класс) 223
Презентация Вариант дифференцированной контрольной работы по теме Квадратные уравнения и неравенства (8 класс) Презентация Вариант дифференцированной контрольной работы по теме Квадратные уравнения и неравенства (8 класс) 140
Презентация по математике Рационал өрнектерді көбейту Презентация по математике Рационал өрнектерді көбейту 196
Древнейшие задачи на прогрессии (9-11кл) Древнейшие задачи на прогрессии (9-11кл) 267
Неравенства и их системы. Неравенства и их системы. 160
Производные тригонометрических функций Производные тригонометрических функций 160
Несовместимые события Несовместимые события 210
Розв’язування задач на обчислення ймовірностей Розв’язування задач на обчислення ймовірностей 165
Шкалы Шкалы 156
Логарифмическая функция и ее приложения Логарифмическая функция и ее приложения 170
Методы решения показательных уравнений и неравенств Методы решения показательных уравнений и неравенств 170
Презентация по алгебре Никольский Подобные одночлены(7 класс) Презентация по алгебре Никольский Подобные одночлены(7 класс) 192
Презентация к уроку математики на тему квадратные корни Презентация к уроку математики на тему квадратные корни 167
Математическая игра для учащихся 7-8 классов Осенние Олимпийские игры Математическая игра для учащихся 7-8 классов Осенние Олимпийские игры 208
Урок геометрии по теме Задачи на построение Урок геометрии по теме Задачи на построение 175
Презентация к уроку математики 7 кл Презентация к уроку математики 7 кл 173
Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) Презентация по алгебре на тему Умножение многочлена на одночлен (7 класс) 185
Тригонометрическая форма записи комплексного числа 10 класс Тригонометрическая форма записи комплексного числа 10 класс 199
Презентация по математике Построение циркулем и линейкой Презентация по математике Построение циркулем и линейкой 174
Презентация по алгебре на тему Квадратные уравнения (8 класс) Презентация по алгебре на тему Квадратные уравнения (8 класс) 165
Арифметическая прогрессия Арифметическая прогрессия 147
Презентация по математике на тему Степень. Степенная функция (11 класс) Презентация по математике на тему Степень. Степенная функция (11 класс) 201