Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Системы счисления

Содержание

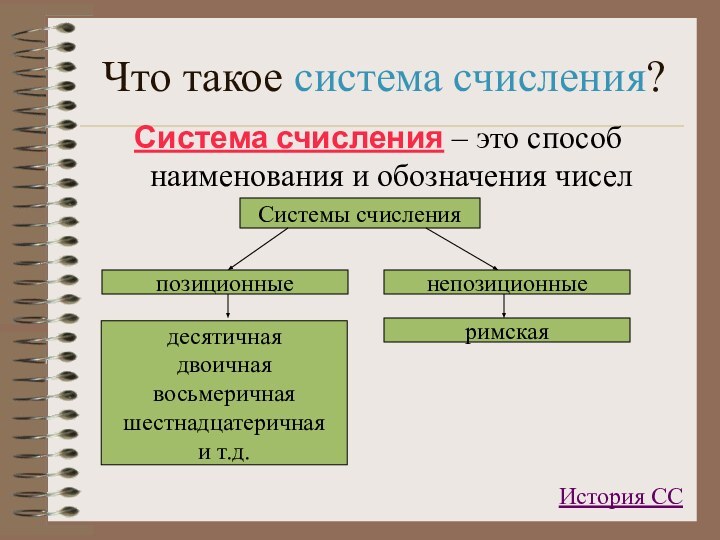
2. Что такое система счисления?Система счисления – это способ наименования и обозначения чиселИстория СС
3. Цифра. Что это?Знаки (символы), используемые в СС для обозначения чисел, называются цифрами
4. Римская система счисленияЯвляется непозиционной, т.е. каждый символ
5. Позиционные системы счисленияОснованием системы может быть
6. Десятичная ССОснование системы – число 10;Содержит 10
7. Двоичная ССОснование системы – 2;Содержит 2 цифры:
8. Правила переводаИз десятичной СС в двоичную СС:Разделить
9. Примеры:27 : 2 = 13 +
10. Задание № 1 Для десятичных чисел
11. 2. Перевод из двоичной системы счисления
12. Задание № 2 Двоичные числа 10110012, 111102, 110110112 перевести в десятичную систему.проверка
13. Восьмеричная ССОснование системы – 8;Содержит 8 цифры:
14. Шестнадцатеричная ССОснование системы – 16;Содержит 16 цифр:
15. Правило перевода целых чисел из десятичной системы
16. Примеры:335 : 16 = 20 + 15
17. Задание № 3-1Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему.проверка
18. Задание № 3-2Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему.проверка
19. Правило перевода дробных чисел из десятичной системы
20. Примеры:0,21 * 8 = 1,68 10,68
21. Задание 3-3Десятичные числа 0,51; 0,125 перевести в 8 и 16 системы счисления.проверка
22. Правило перевода из p-i системы счисления
23. Задание № 4-1Восьмеричные числа 41, 520, 306 перевести в десятичную систему.проверка
24. Задание № 4-2Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему.проверка
25. Связь систем счисления
26. Переводы в системах счисления с основанием кратным 2
27. Правило перевода из двоичной системы счисления в
28. Задание № 5Двоичные числа 101011,112
29. Правило перехода из двоичной системы счисления в
30. Задание № 6Двоичные числа 101011112
31. Правило перевода из восьмеричной системы счисления в
32. Задание № 7Восьмеричные числа 26, 702, 4017 перевести в двоичную систему.проверка
33. Правило перевода из шестнадцатеричной системы счисления в
34. Задание № 8Шестнадцатеричные числа C3; B0,96; E38 перевести в двоичную систему.проверка
35. Ответы к заданию №1
36. Ответы к заданию № 2
37. Ответы к заданию № 3-1
38. Ответы к заданию № 3-2
39. Ответы к заданию № 3-3
40. Ответы к заданию № 4-1
41. Ответы к заданию № 4-2
42. Ответы к заданию № 5
43. Ответы к заданию № 6
44. Ответы к заданию № 7
45. Скачать презентацию
46. Похожие презентации

Что такое система счисления?Система счисления – это способ наименования и обозначения чиселИстория СС

Цифра. Что это?Знаки (символы), используемые в СС для обозначения чисел, называются цифрами

Римская система счисленияЯвляется непозиционной, т.е. каждый символ обозначает всегда одно и тоже

Позиционные системы счисленияОснованием системы может быть любое натуральное число, большее единицы;Основание

Десятичная ССОснование системы – число 10;Содержит 10 цифр: 0, 1, 2,

Двоичная ССОснование системы – 2;Содержит 2 цифры: 0; 1;Любое двоичное число можно

Правила переводаИз десятичной СС в двоичную СС:Разделить десятичное число на 2.

Задание № 1 Для десятичных чисел 341; 125; 1024; 4095 выполни

2. Перевод из двоичной системы счисления в десятичнуюДля

Задание № 2 Двоичные числа 10110012, 111102, 110110112 перевести в десятичную систему.проверка

Восьмеричная ССОснование системы – 8;Содержит 8 цифры: 0; 1; 2; 3; 4;

Шестнадцатеричная ССОснование системы – 16;Содержит 16 цифр: от 0 до 9;

Правило перевода целых чисел из десятичной системы счисления в p-i Разделить десятичное

Задание № 3-1Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему.проверка

Задание № 3-2Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему.проверка

Правило перевода дробных чисел из десятичной системы счисления в p-i Умножить десятичную

Примеры:0,21 * 8 = 1,68 10,68 * 8 = 5,44

Задание 3-3Десятичные числа 0,51; 0,125 перевести в 8 и 16 системы счисления.проверка

Правило перевода из p-i системы счисления в q-i систему счисленияДля перевода

Задание № 4-1Восьмеричные числа 41, 520, 306 перевести в десятичную систему.проверка

Задание № 4-2Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему.проверка

Переводы в системах счисления с основанием кратным 2

Правило перевода из двоичной системы счисления в восьмеричнуюРазбить двоичное число на триады

Задание № 5Двоичные числа 101011,112 ; 110011001,102

Правило перехода из двоичной системы счисления в шестнадцатеричнуюРазбить двоичное число на тетрады

Правило перевода из восьмеричной системы счисления в двоичнуюКаждую восьмеричную цифру заменить соответствующим

Задание № 7Восьмеричные числа 26, 702, 4017 перевести в двоичную систему.проверка

Правило перевода из шестнадцатеричной системы счисления в двоичнуюКаждую шестнадцатеричную цифру заменить двоичным

Задание № 8Шестнадцатеричные числа C3; B0,96; E38 перевести в двоичную систему.проверка

Слайды презентации

Слайд 2 Что такое система счисления?
Система счисления – это способ

наименования и обозначения чисел
История СС

Слайд 3 Цифра. Что это?
Знаки (символы), используемые в СС для

обозначения чисел, называются цифрами

Слайд 4 Римская система счисления
Является непозиционной, т.е. каждый символ обозначает

Римская система счисленияЯвляется непозиционной, т.е. каждый символ обозначает всегда одно и

всегда одно и тоже число;
Цифры обозначаются латинскими буквами:
I,

V, X, L, C, D, M
(1, 5, 10, 50, 100, 500, 1000)
Например: XXX – 30; XLI - 41

Слайд 5 Позиционные системы счисления
Основанием системы может быть любое натуральное

число, большее единицы;
Основание ПСС – это количество цифр, используемое

для представления чисел;
Значение цифры зависит от ее позиции, т.е. одна и та же цифра соответствует разным значениям в зависимости от того, в какой позиции числа она стоит;
Например: 888: 800; 80; 8
Любое позиционное число можно представить в виде суммы степеней основания системы.

Слайд 6 Десятичная СС
Основание системы – число 10;
Содержит 10 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8,

9;
Любое десятичное число можно представить в виде суммы степеней числа 10 – основания системы;

Слайд 7 Двоичная СС
Основание системы – 2;
Содержит 2 цифры: 0;

Двоичная ССОснование системы – 2;Содержит 2 цифры: 0; 1;Любое двоичное число

1;
Любое двоичное число можно представить в виде суммы степеней

числа 2 – основания системы;
Примеры двоичных чисел: 111001012; 101012;

Слайд 8 Правила перевода
Из десятичной СС в двоичную СС:
Разделить десятичное

число на 2. Получится частное и остаток.
Частное опять разделить

на 2. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

Слайд 9 Примеры:

27 : 2 = 13 + 1
13

: 2 = 6 + 1
6

: 2 = 3 + 0
3 : 2 = 1 + 1
1 : 2 = 0 + 1

Слайд 10 Задание № 1

Для десятичных чисел 341;

125; 1024; 4095 выполни перевод в двоичную систему счисления.

проверка

Слайд 11 2. Перевод из двоичной системы счисления

2. Перевод из двоичной системы счисления в десятичнуюДля перехода

в десятичную
Для перехода из двоичной системы счисления в

десятичную необходимо двоичное число представить в виде суммы произведений цифр числа на основание (2) в степени, соответствующей месту цифры и найти ее десятичное значение.
Пример:

Слайд 12 Задание № 2
Двоичные числа 10110012, 111102,

110110112 перевести в десятичную систему.

проверка

Слайд 13 Восьмеричная СС
Основание системы – 8;
Содержит 8 цифры: 0;

Восьмеричная ССОснование системы – 8;Содержит 8 цифры: 0; 1; 2; 3;

1; 2; 3; 4; 5; 6; 7;
Любое восьмеричное число

можно представить в виде суммы степеней числа 8 – основания системы;
Примеры восьмеричных чисел: 21058; 734618;

Слайд 14 Шестнадцатеричная СС
Основание системы – 16;
Содержит 16 цифр: от

0 до 9; A; B; C; D; E; F;
Любое

шестнадцатеричное число можно представить в виде суммы степеней числа 16 – основания системы;
Примеры шестнадцатеричных чисел: 21AF316; B09D16;

Слайд 15 Правило перевода целых чисел из десятичной системы счисления

Правило перевода целых чисел из десятичной системы счисления в p-i Разделить

в p-i
Разделить десятичное число на p. Получится частное

и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньше p.
Записать остатки в обратном порядке. Полученное число и будет p-i записью исходного десятичного числа.

Слайд 16 Примеры:
335 : 16 = 20 + 15
20

: 16 = 1 + 4

1 : 16 = 0 + 1

(F)

Слайд 17 Задание № 3-1
Десятичные числа 421, 5473, 1061 перевести

в восьмеричную систему.

проверка

Слайд 18 Задание № 3-2
Десятичные числа 512, 302, 2045 перевести

в шестнадцатеричную систему.
проверка

Слайд 19 Правило перевода дробных чисел из десятичной системы счисления

Правило перевода дробных чисел из десятичной системы счисления в p-i Умножить

в p-i
Умножить десятичную дробь на p.
Целую часть

выписать, с дробной продолжить умножение до тех пор, пока она не станет равной 0 или не выделится в период
Выписать целые части сверху-вниз. Полученное число и будет p-i записью исходного десятичного числа.

Слайд 20 Примеры:
0,21 * 8 = 1,68 1
0,68 *

Примеры:0,21 * 8 = 1,68 10,68 * 8 = 5,44 50,44

8 = 5,44 5
0,44 * 8 = 3,52

3
0,52 * 8 = 4,16 4

0,35 * 16 = 5,6 5
0,6 * 16 = 9,6 9
0,6 * 16 = 9,6 9

Слайд 21 Задание 3-3
Десятичные числа
0,51; 0,125
перевести в 8

и 16 системы счисления.
проверка

Слайд 22 Правило перевода из p-i системы счисления в q-i

систему счисления
Для перевода из p-i системы счисления в q-i

число надо сначала перевести из p-i системы счисления в 10 систему счисления (развернутая форма числа), а затем из 10СС в q-i (деление целой и умножение дробной части)

123,547→ 3СС

123,27 = 1*72 + 2*71 + 3*70 +2*7-1 + = 49+14+3+2\7=66,2910

66 : 3 = 22 + 0
22 : 3 = 7 + 1
7 : 3 = 2 + 1
2 : 3 = 0 + 1

0,26 * 3 = 0,78 0
0,78 * 3 = 2,34 2
0,34 * 3 = 1,02 1
0.02 * 3 = 0,06 0

123,27 = 111,02173