формул синуса и косинуса двойного угла .
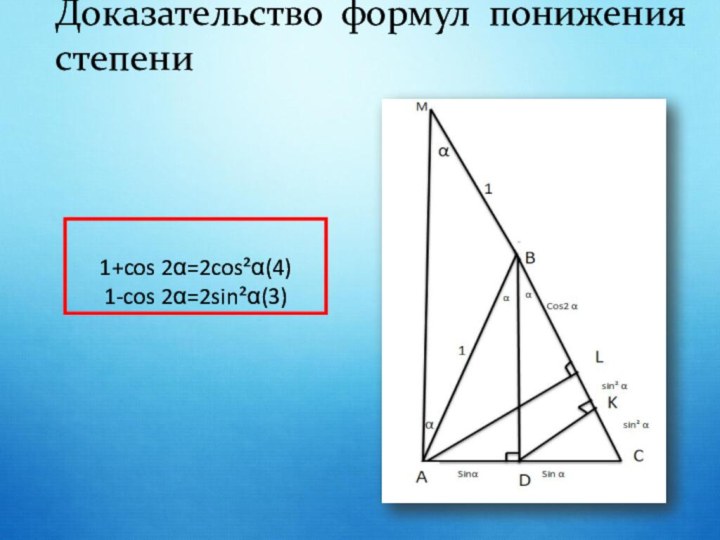
Доказательство формул понижения
степени.Доказательство формулы синуса и косинуса суммы двух углов.
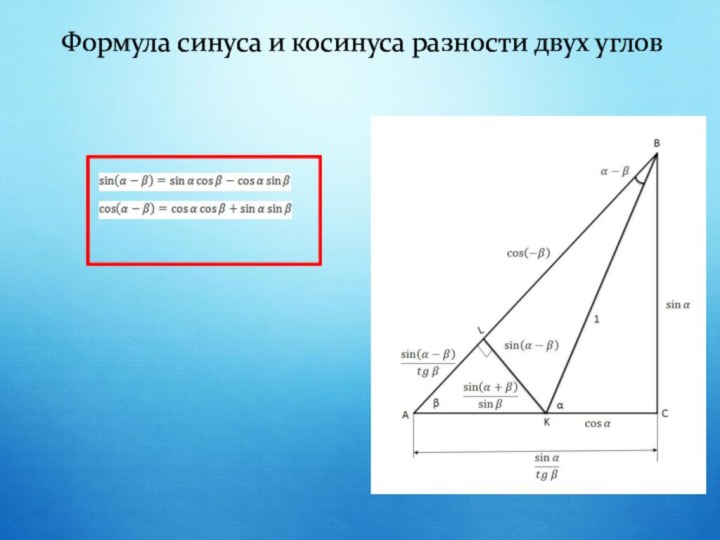
Доказательство формулы синуса и косинуса разности двух углов.
Примеры.
Используемая литература .
Содержание




![Тригонометрические формулы Применения тригонометрии[adcos(t) + ddt , bdsin(t), cdt + edt2]Феликс](/img/tmb/7/649511/9936be4aa03c281ec320f256d2a56203-720x.jpg)