- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определённый интеграл
Содержание
- 2. Задачи, приводящие к понятию определённого интеграла.
- 3. Задача 1. В декартовой прямоугольной системе координат х0у
- 4. ух0y=f(x)x1x2x3хn-1xkxk+1abРазобьём отрезок [а;b] (основание криволинейной трапеции) на
- 5. ух0y=f(x)x1x2x3xn-1xkxk+1abРассмотрим отдельно k-ый столбик, т.е. криволинейную трапецию,
- 6. ух0y=f(x)x1x2x3xn-1xkxk+1abЕсли теперь сделать то же самое со
- 7. Принято считать, что искомая площадь есть предел последовательности (Sn)
- 8. Задача 2 (о вычислении массы стержня). Дан прямолинейный
- 9. Как известно из курса физики, m =
- 10. 4) Найдём приближённое значение массы m стержня:m
- 11. Задача 3 (о перемещении точки). По прямой движется
- 12. Если бы движение было равномерным, то задача
- 13. ПОДВЕДЁМ ИТОГИ.Три различные задачи привели при их
- 14. Понятие определённого интеграла.Дадим определение той модели, которая
- 15. Результат, полученный в 1 задаче, можно переписать
- 16. ФормулаНьютона - Лейбница
- 17. Скачать презентацию
- 18. Похожие презентации



![Определённый интеграл ух0y=f(x)x1x2x3хn-1xkxk+1abРазобьём отрезок [а;b] (основание криволинейной трапеции) на n равных частей; это разбиение](/img/tmb/6/588488/878ab4c1d0b780f0f5870251a25b6a80-720x.jpg)










![Определённый интеграл Теорема. Если функция y=f(x) непрерывна на отрезке [a;b], то справедлива формула Где](/img/tmb/6/588488/9df08dd4f1bf4237b1680b77ba94370d-720x.jpg)
Слайд 4
у
х
0
y=f(x)
x1
x2
x3
хn-1
xk
xk+1
a
b
Разобьём отрезок [а;b] (основание криволинейной трапеции) на n
равных частей; это разбиение осуществим с помощью точек х1,
х2, х3, …, xk, xk+1, …, xn-1.Тогда заданная трапеция разобьётся на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.
Слайд 5
у
х
0
y=f(x)
x1
x2
x3
xn-1
xk
xk+1
a
b
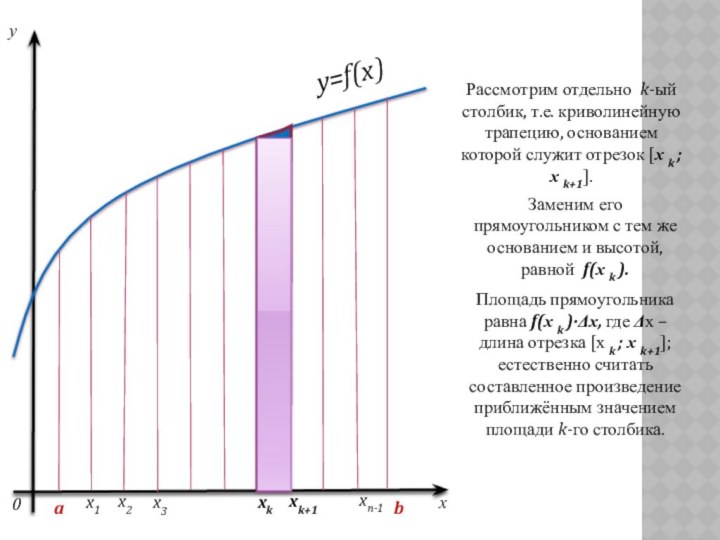
Рассмотрим отдельно k-ый столбик, т.е. криволинейную трапецию, основанием
которой служит отрезок [х k ; х k+1].
Площадь
прямоугольника равна f(х k )·Δх, где Δх – длина отрезка [х k ; х k+1]; естественно считать составленное произведение приближённым значением площади k-го столбика.Заменим его прямоугольником с тем же основанием и высотой, равной f(х k ).
Слайд 6
у
х
0
y=f(x)
x1
x2
x3
xn-1
xk
xk+1
a
b
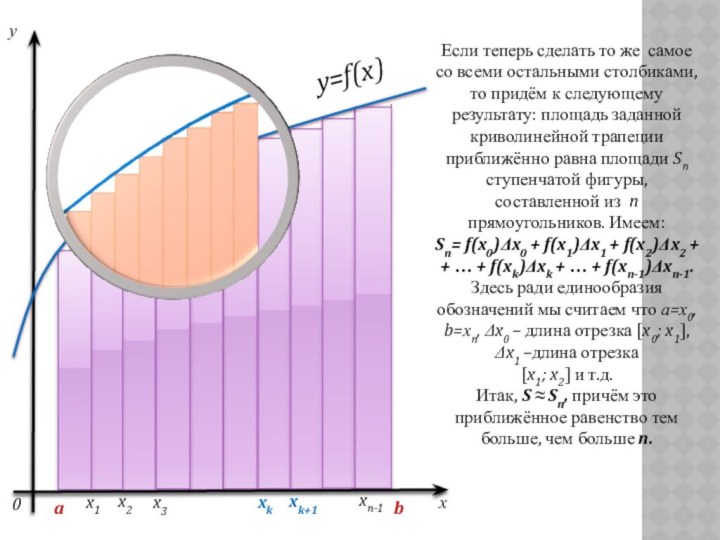
Если теперь сделать то же самое со всеми
остальными столбиками, то придём к следующему результату: площадь заданной
криволинейной трапеции приближённо равна площади Sn ступенчатой фигуры, составленной из n прямоугольников. Имеем:Sn= f(x0)Δx0 + f(x1)Δx1 + f(x2)Δx2 + + … + f(xk)Δxk + … + f(xn-1)Δxn-1.
Здесь ради единообразия обозначений мы считаем что а=х0, b=хn, Δx0 – длина отрезка [x0; x1], Δx1 –длина отрезка
[x1; x2] и т.д.
Итак, S ≈ Sn, причём это приближённое равенство тем больше, чем больше n.
Слайд 8
Задача 2 (о вычислении массы стержня).
Дан прямолинейный неоднородный
стержень, плотность в точке х вычисляется по формуле р=р(x).
Найти массу стержня.Слайд 9 Как известно из курса физики, m = ρ·V,
но этот закон действует только для однородных тел, т.е.
в тех случаях, когда плотность постоянна. Для неоднородного стержня используется тот же метод, что был применён при решении задачи 1.х
хn-1=b
xk+1
xk
x2
x1
х0=a
I I I I I I I
Разобьём отрезок [а;b] на n равных частей;
Рассмотрим отдельно k-ый участок [х k ; х k+1] и будем считать, что плотность во всех точках этого участка постоянна, а именно такая, как, например, в точке х k . Итак, считаем, что ρ=ρ(xk).
Найдём приближённое значение массы mk k-го участка:
mk≈ ρ(xk)·Δxk,
Где Δxk, как и в предыдущей задаче, - длина отрезка [х k ; х k+1].
Слайд 10
4) Найдём приближённое значение массы m стержня:
m ≈
Sn,
Где Sn= m0 + m1 + m2 + …
+ mk + … + mn-1 =ρ(x0)Δx0 + ρ(x1)Δx1 + ρ(x2)Δx2 + + … + ρ(xk)Δxk + … + ρ(xn-1)Δxn-1.
5) Точное значение массы стержня вычисляется по формуле
Слайд 11
Задача 3 (о перемещении точки).
По прямой движется точка.
Зависимость скорости от времени выражается формулой v=v(t); пусть для
определённости v(t)>0. Найти перемещение точки за промежуток времени [a;b].Слайд 12 Если бы движение было равномерным, то задача решалась
бы очень просто: s = vt, т.е. s =
v(b-a). Для неравномерного движения приходится использовать те же идеи, на которых было основано решение двух предыдущих задач.Разобьём отрезок [а;b] на n равных частей.
Рассмотрим отдельно k-ый участок [t k ; t k+1] и будем считать, что скорость на этом промежутке времени постоянна, а именно такая, как, например, в момент времени t k . Итак, считаем, что v = v (t k).
Найдём приближённое значение перемещения точки sk за промежуток времени [t k ; t k+1] :
sk ≈ v(tk)·Δ tk,
4) Найдём приближённое значение перемещения s:
s ≈ Sn,
Где Sn= s 0 + s 1 + s 2 + … + s k + … + s n-1 =
v(t0)Δt0 + v(t1)Δt1 + v(t2)Δt2 + + … + v(tk)Δtk + … + v(tn-1)Δtn-1.
5) Точное значение перемещения вычисляется по формуле:
Слайд 13
ПОДВЕДЁМ ИТОГИ.
Три различные задачи привели при их решении
к одной и той же математической модели. Многие задачи
из различных областей науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить, т.е.:а) присвоить ей новый термин;
б) ввести для неё обозначение;
в) научиться с ней работать.
Этим и займёмся.
Слайд 14
Понятие определённого интеграла.
Дадим определение той модели, которая была
построена в трёх рассмотренных задачах для функции y =
f(x), непрерывной (но обязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а;b]:Разбивают отрезок [а;b] на n равных частей.
Составляют сумму:
Sn= f(x0)Δx0 + f(x1)Δx1 + f(x2)Δx2 + + … + f(xk)Δxk + … + f(xn-1)Δxn-1.
3) Вычисляют lim Sn
n→∞
В курсе математического анализа доказано, что при указанных условиях этот предел существует. Его называют определённым интегралом от функции y = f(x) по отрезку [а;b] и обозначают так:
Слайд 15
Результат, полученный в 1 задаче, можно переписать так:
Где
S – площадь криволинейной трапеции. В этом состоит геометрический
смысл определённого интеграла.Из решения задачи 2 следует, что масса m неоднородного стержня с плотностью ρ(x) вычисляется по формуле
В этом состоит физический смысл определённого интеграла.
Из решения задачи 3 следует, что перемещение s точки, движущейся по прямой со скоростью v=v(t), за промежуток времени от t=a до t=b, вычисляется по формуле
Это ещё одно физическое истолкование определённого интеграла.





























