- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод математической индукции
Содержание
- 2. В основе математического исследования лежитДедуктивный методИндуктивный метод
- 3. Дедуктивный методДедуктивный метод – это рассуждение, исходным
- 4. Индуктивный методИндуктивный метод – рассуждение, при котором,
- 5. Пример рассуждения по индукцииТребуется установить, что каждое
- 6. 4=2+2; 6=3+3; 8=3+5; 10=5+5; ...;92=3+89; 94=5+89; 96=7+89;
- 7. Это был пример полной индукции, когда общее
- 8. Пример 1
- 9. Пример 2
- 10. Итак, неполная индукция не считается в математике
- 11. Метод математической индукции
- 14. Составляющие метода математической индукцииПусть нужно доказать справедливость
- 15. Скачать презентацию
- 16. Похожие презентации
В основе математического исследования лежитДедуктивный методИндуктивный метод












Слайд 3
Дедуктивный метод
Дедуктивный метод – это рассуждение, исходным моментом
которого является общее утверждение, а заключительным – частный результат.
Слайд 4
Индуктивный метод
Индуктивный метод – рассуждение, при котором, опираясь
на ряд частных результатов приходят к одному общему выводу.
Слайд 5
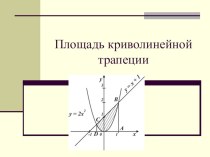
Пример рассуждения по индукции
Требуется установить, что каждое четное
число в пределах от 4 до 100 можно представить
в виде суммы двух простых чисел. Для этого переберем все интересующие нас числа и выпишем соответствующие суммы:
Слайд 6
4=2+2; 6=3+3; 8=3+5; 10=5+5; ...;
92=3+89; 94=5+89; 96=7+89; 98=9+89;
100=3+97.
Эти
49 равенств (мы выписали только 9 из них) показывают,
что утверждение о том, что любое четное число от 4 до100 можно представить в виде суммы двух простых чисел, верно и было доказано путем перебора всех частных случаев.Слайд 7 Это был пример полной индукции, когда общее утверждение
доказывается для конечного множества элементов при рассмотрении каждого из
этих элементов.Но чаще общее утверждение относится не к конечному, а к бесконечному множеству. В таких случаях общее утверждение может быть угаданным, полученным неполной индукцией. Оно может оказаться верным или неверным.
Слайд 10 Итак, неполная индукция не считается в математике методом
строгого доказательства, т.к. может привести к ошибке. Во многих
случаях, когда доказательство найти трудно, обращаются к особому методу рассуждений, который называется методом математической индукции.
Слайд 14
Составляющие метода математической индукции
Пусть нужно доказать справедливость А(n),
где n – любое натуральное число.
Для этого сначала проверим
справедливость А(n) для n=1(базис математической индукции).Затем докажем, что для любого натурального числа k справедливо следующее: если А(k) – справедливо, то А(k+1), тоже справедливо(индукционный шаг).
Делаем вывод, что А(n) справедливо для любого n.