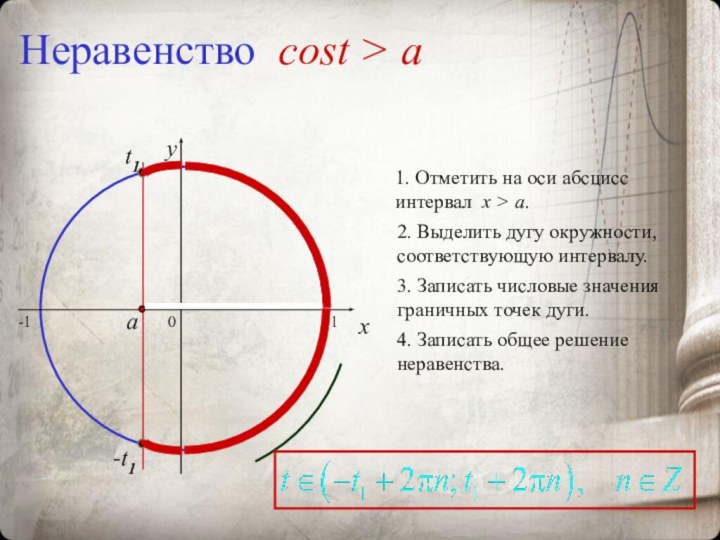
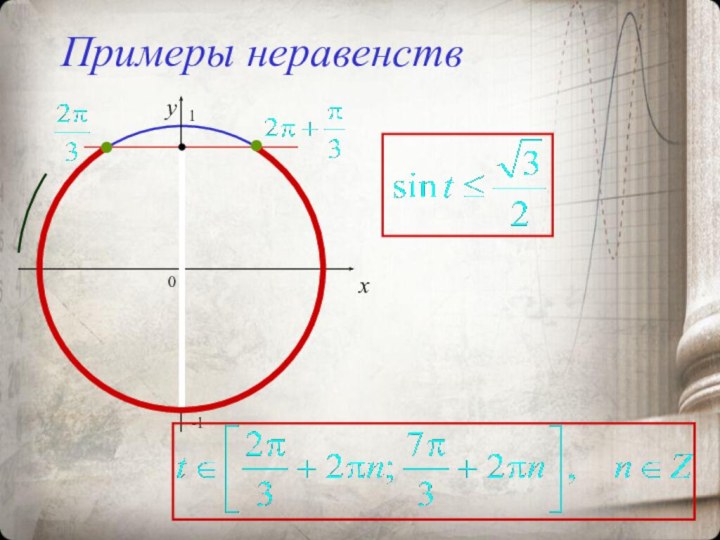
тригонометрических функций. Рассмотреть их графики и свойства.
Ввести понятие тригонометрического
уравнения и неравенства.Научиться решать простейшие уравнения и неравенства и отдельные виды тригонометрических уравнений, которые приводятся к простейшим.
Знать:
формулы общего решения простейших тригонометрических уравнений
Уметь:
решать тригонометрические уравнения, простейшие тригонометрические неравенства



![Тригонометрические уравнения и неравенства Область опрделения функции y = arcsin x – отрезок [-1;1]Область значений –](/img/tmb/6/577436/9ade0eecb0af3490ab0e668b4d859791-720x.jpg)

![Тригонометрические уравнения и неравенства Область опрделения функции y = arccos x – отрезок [-1;1]Область значений –](/img/tmb/6/577436/ac6a5a8212d655792cc0de1d2fb3384c-720x.jpg)