Слайд 2
Задачи:
1) Дать определение числа π
2) Выяснить историю вычисления
π.
3) Провести эксперимент по вычислению приближенного значения отношения длины
окружности к диаметру.
4) Рассмотреть некоторые факты из «современной биографии» числа π. .
На историческом материале показать важность проблемы вычисления числа π, раскрыть необходимость точных вычислений значения π на современном этапе, а также показать огромное трудолюбие и работоспособность учёных, занимавшихся этим вопросом в течение многих столетий.
Цели:
Слайд 3
Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами
Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы
нам не ошибаться,
Чтоб окружность верно счесть,
Надо только постараться
И запомнить все как есть
Три — четырнадцать —
пятнадцать — девяносто два и
шесть!
С.Бобров
Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле
Слайд 4
Число π — математическая константа, выражающая отношение длины
окружности к длине ее диаметра.
Если принять диаметр окружности за
единицу, то длина окружности и есть число π.
В цифровом выражении π начинается как 3,141592 и имеет бесконечную математическую продолжительность.
Определение
Слайд 5
Первая тысяча знаков приближённого значения

числа «ПИ» :
3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642019
Слайд 6
Интересные факты
Неофициальный праздник «День числа Пи» отмечается 14
марта, которое в американском формате дат (месяц/день) записывается как
3.14, что соответствует приближённому значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
В штате Юта (США) был принят закон с очень короткой формулировкой "Пи равно трем", а в штате Индиана властями было официально назначено, что Пи равно 4.
Слайд 7
История числа π
Проблеме π – 4000 лет. Исследователи
древних пирамид установили, что частное, полученное от деления суммы
двух сторон основания на высоту пирамиды, выражается числом 3,1416.
Слайд 8
=3,1605
Папирус АХМЕСА
2000 до н.э.
В знаменитом папирусе Ахмеса приводится
такое указание для построения квадрата, равного по площади кругу:
« Отбрось от диаметра его девятую часть и
построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу»
Из этого следует, что у Ахмеса π ≈ 3,1605.
Так началась письменная история числа π:
Слайд 9
В Вавилоне в v веке до н. э.
пользовались числом 3 1/8≈ 3,1215,
а в
древней Греции числом (√2+√3)≈3,1462643.
В индийских «сутрах» VI–V в до н. э. имеются правила, из которых вытекает, что π ≈3,008.
Наиболее древняя формулировка нахождения приближённого значения отношения длины окружности к диаметру содержится в стихах индийского математика Ариабхаты (V-VI в)
Прибавь четыре к сотне и умножь на восемь,
Потом ещё шестьдесят две тысячи прибавь.
Когда поделишь результат на двадцать тысяч,
Тогда откроется тебе значение
Длины окружности к двум радиусам отношенья, т. е.
длина окружности 62832
__________________ = ______ ≈3,1416
диаметр 20000
Слайд 10
Архимед ( III в. до н. э.) для
оценки числа π вычислял периметры вписанных и описанных от
6-ти до 96-ти многоугольников.
Такой метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет.
10 1
Архимед получил 3 ---- < π < 3 ---- ,
т. е. π≈ 3, 1418. 71 7
Долгое время все пользовались значением
числа, равным
22
----
7
Слайд 11
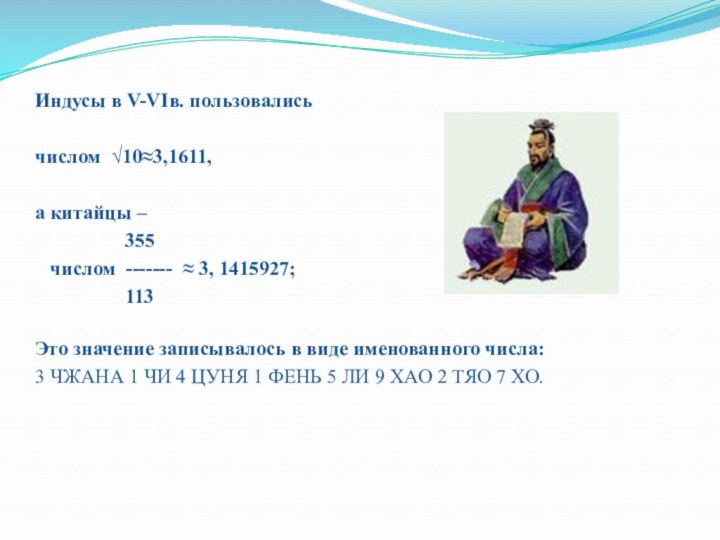
Индусы в V-VIв. пользовались
числом √10≈3,1611,
а китайцы
–
355
числом ------- ≈ 3, 1415927;
113
Это значение записывалось в виде именованного числа:
3 ЧЖАНА 1 ЧИ 4 ЦУНЯ 1 ФЕНЬ 5 ЛИ 9 ХАО 2 ТЯО 7 ХО.
Слайд 12
В XV в. иранский математик Ал-Каши нашел значение
π с 16-ю верными знаками, рассмотрев вписанный и описанный
многоугольники с
3*228 сторонами.
=3,141592653589793
Слайд 13
Андриан Ван Ромен (Бельгия) в XVI получил
17 верных десятичных знаков, а голландский вычислитель- Лудольф ван-
Цейлен (1540-1610), вычисляя π, дошел до многоугольников с 6020 сторонами и получил 35 верных знаков для π. Ученый обнаружил большое терпение и выдержку, затратив несколько лет на определение числа π. В его честь современники назвали π «Лудольфово число».
Согласно завещанию, на его надгробном камне было высечено найденное им значение π.
Слайд 14
Обозначение π (первая буква в греческом слове
окружность, периферия) впервые встречается у английского математика Уильяма Джонса
(1706г.),
а после опубликования работы Леонарда Эйлера (1736г. С.-Петербург), вычислившего значение π с точностью до 153 десятичных знаков, обозначение π становится общепринятым.
Слайд 15
π — иррациональное число, то есть его значение
не может быть точно выражено в виде дроби m/n,
где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. Иррациональность числа π была впервые доказана Иоганном Ламбертом в 1767 году путём разложения числа в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π и π2.
π — трансцендентное число, это означает, что оно не может быть корнем какого-либо многочлена с целыми коэффициентами. Трансцендентность числа π была доказана в 1882 году профессором Кенигсбергского, а позже Мюнхенского университета Линдеманом. Доказательство упростил Феликс Клейн в 1894 году.
Слайд 16
Проведём практическую работу.
Возьмём 5 любых предметов: теннисный мяч,
стакан, кружку, баночку, банку для теннисных мячей.
Слайд 17
Обвяжем предметы ниткой и таким образом мы измерим
длину окружности.
Слайд 19
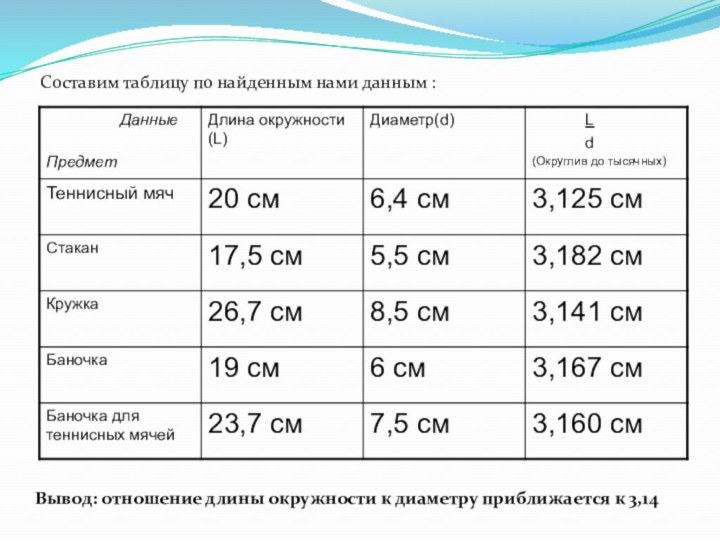
Составим таблицу по найденным нами данным :
Вывод: отношение
длины окружности к диаметру приближается к 3,14
Слайд 20
О вычислениях значения числа π на современном этапе
С
появлением ЭВМ значения числа π было вычислено с достаточно
большой точностью. В США, например, был получен результат с более 30 млн. знаков. Если распечатать значение числа, полученное в США, то оно займёт 30 томов по 400 страниц в каждом.
Вычисление такого числа знаков для π не имеет практического значения, а лишь показывает огромное преимущество и совершенство современных средств и методов вычисления по сравнению со старыми.
Слайд 21
С помощью компьютера было вычислено десятичных знаков:
1949 год
— 2037 десятичных знаков
1958 год — 10000 десятичных
знаков
1961 год — 100000 десятичных знаков
1973 год — 10000000 десятичных знаков
1986 год — 29360000 десятичных знаков
1987 год — 134217000 десятичных знаков
1989 год — 1011196691 десятичный знак
1991 год — 2260000000 десятичных знаков
1994 год — 4044000000 десятичных знаков
1995 год — 4294967286 десятичных знаков
1997 год — 51539600000 десятичных знаков
1999 год — 206 158 430 000 десятичных знаков.
Суперкомпьютер в сентябре 1999 года работал 37 часов 21 минут 4 секунды, используя 865 Гбайт памяти для основной задачи, и 46 часов и 816 Гбайт для вспомогательной оптимизации вычислений.
Слайд 22
В 2009 году французский программист Фабрис Беллар поставил
рекорд вычисления числа Пи с точностью до 2,7 трлн
знаков после запятой. Что самое удивительное, он сделал это на своём персональном компьютере под управлением Fedora 10.
Достижение Беллара показало, что не обязательно иметь суперкомпьютер для таких вычислений, и его коллеги решили сделать компьютер помощнее и перекрыть достижение француза.
2 августа 2010 года американский студент Александр Йи и японский исследователь Сигэру Кондо рассчитали последовательность с точностью в 5 триллионов цифр после запятой.
Слайд 23
Вывод:
Я хотела узнать об истории вычисления числа Пи,
и думаю, что достигла поставленной цели.
Точное значение числа
Пи в современном мире представляет собой не только собственную научную ценность, но и используется для очень точных вычислений (например, орбиты спутника, строительства гигантских мостов), а также оценки быстродействия и мощности современных компьютеров.